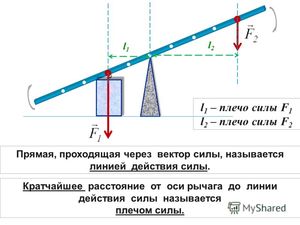
точка приложения силы реакции опоры

Силы в механике

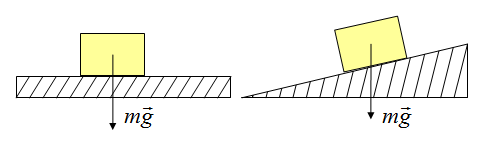
1. Сила тяжести.

На любое тело, находящееся вблизи поверхности земли или лежащее на земле действует сила, равная произведению массы тела на ускорение свободного падения:.

2. Сила реакции опоры (нормальной реакции, упругости опоры)

Сила, действующая о стороны опоры на лежащее на ней тело. Всегда направлена перпендикулярно поверхности соприкосновения тела и опоры.

\vec –сила реакции опоры.

Если тело лежит на внутренней поверхности сферы, сила \vec направлена к центру сферы.

Если тело лежит на внешней поверхности сферы, сила \vec направлена от центра сферы.

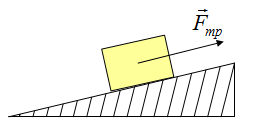
3. Сила натяжения нити

Сила, действующая со стороны нити (веревки, каната, троса, стержня и т.п.) на тело, которое висит на нити (веревке и т.п.). Направлена вдоль нити (и т.п.).

\vec–Сила натяжения нити.

4. Вес тела

Определение: – это сила, с которой тело давит на опору или растягивает подвес.

Вес тела равен по модулю силе реакции опоры или силе натяжения нити, направлен в противоположную сторону и приложен к другому телу: либо опоре, либо нити.

\vec –сила реакции опоры;

5. Сила трения

a) Сила трения скольжения

Сила трения скольжения направлена противоположно относительной скорости тел и не зависит от площади соприкосновения поверхностей.

\vec_ <тр>–сила трения скольжения.

Модуль силы трения равен произведению коэффициента трения скольжения на модуль силы реакции опоры:

\mu –коэффициент трения скольжения.

b) Сила трения качения

Действует на тело, которое не скользит, а катится по некоторой поверхности.

\vec_ <тр>–сила трения качения.

\mu _ <1>–коэффициент трения качения.

Коэффициент трения качения много меньше коэффициента трения скольжения

c) Сила трения покоя

Действует на тело, лежащее неподвижно на некоторой поверхности, которое мы пытаемся сдвинуть с места. Противоположно направлена внешней силе и равна ей по модулю.

\vec_ <тр.п.>– сила трения покоя.

\vec_ <внешн.>– внешняя сила.

6. Схема решения задач

a) Нарисовать все силы, приложенные ко всем телам системы;

b) Выбрать системы отсчета (можно свою для каждого тела);

c) Спроектировать силы на оси;

d) Записать уравнения для второго закона Ньютона в проекциях для всех тел системы;

e) Записать кинематические связи, то есть связи между скоростями и ускорениями различных тел системы;

Источник

Сила реакции опоры

Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.

Тело находится на выпуклой или вогнутой поверхности

Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой \(\vec\). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.

Примечания:

\(\vec \left( H \right) \) – сила, с которой опора действует на тело.

Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.

Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция \(\vec\) направлена по радиусу внутрь сферической поверхности к ее центру.

Тело опирается на поверхность в двух точках

На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.

В точках соприкосновения поверхность отвечает телу силой \(\vec\) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.

Cилы реакции \(\vec>\) и \(\vec>\) имеют различные направления и в общем случае не равны по модулю.

Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.

Как рассчитать силу нормальной реакции

Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.

Примечание: Сила реакции \(\vec\) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.

Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.

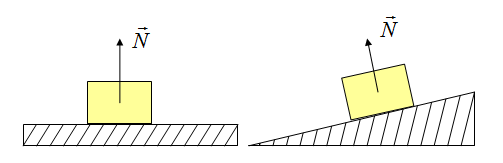
На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.

Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.

По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.

\(m \vec \left( H \right) \) – сила, с которой тело действует на опору;

\(\vec \left( H \right) \) – сила, с которой опора отвечает телу;

Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы \(m \vec\) на ось — это \(mg_\), она будет направлена противоположно реакции опоры \(\vec\) и численно равна ей.

Примечание: Выражение «численно равна» нужно понимать, как «длины векторов равны».

\(\alpha \left(\text <рад>\right) \) – угол между силой \(mg\) и осью Oy.

Источник

Точка приложения силы реакции опоры

Закон всемирного тяготения. Вес тела

Анализируя законы Кеплера, описывающие движение планет, И. Ньютон в 1667 году пришёл к открытию закона всемирного тяготения:

Все тела во Вселенной взаимно притягиваются друг к другу с силами прямо пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними.

В такой форме закон справедлив только для двух тел, которые можно считать материальными точками. Однако можно доказать, что для двух однородных тел шарообразной формы эта форма записи закона тоже справедлива.

Измерить величину гравитационной постоянной удалось английскому физику Г. Кавендишу в 1798 году.

С помощью крутильных весов и свинцовых шаров ему удалось получить значение гравитационной постоянной:

Силой тяжести называют силу, с которой тело притягивается к планете:

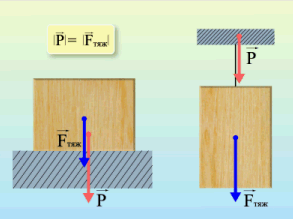
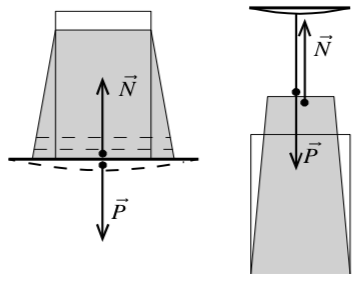Рис. 9

На рисунке 9 тело не касается опоры для того, чтобы показать, что вес приложен к опоре, а сила реакции опоры к телу. В действительности площадь реального соприкосновения твёрдых тел невелика. Большей частью между телами находится тонкий слой воздуха.

Вполне очевидно, что если опоры нет, то и веса тело иметь не будет. Такое случится в том случае, если тело движется под действием только одной силы – силы тяготения.

Невесомостью называют состояние тела, когда оно движется под действием только силы тяготения.

Так же легко понять, что если на тело действует две силы (сила тяжести и сила реакции опоры), то эти силы не обязательно равны друг другу. Одна из них может быть больше другой.

Источник

I. Механика

Тестирование онлайн

Что надо знать о силе

Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!

Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.

Сила тяжести

На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.

Сила трения

Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

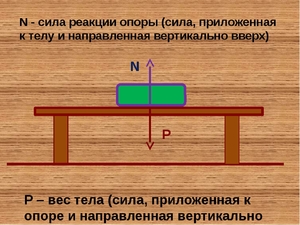
Сила реакции опоры

Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».

Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.

Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как

Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

Сила упругости

Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.

Подробнее о свойствах твердых тел здесь.

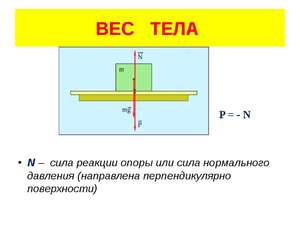
Вес тела

Формулы определения веса нет. Обозначается эта силы буквой .

Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

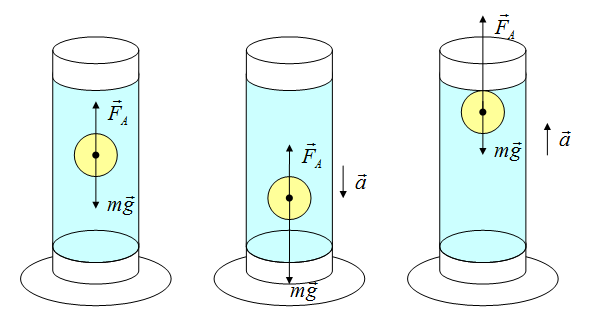
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила

Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

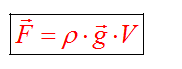
В воздухе силой Архимеда пренебрегаем.

Электрические силы

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.

Схематичное обозначение действующих на тело сил

Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.

Главное запомнить

1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы

Силы трения*

Трение качения определяется по формуле

Сила сопротивления возникает при движении тела в жидкости или в газе. Величина силы сопротивления зависит от размеров и формы тела, скорости его движения и свойств жидкости или газа. При небольших скоростях движения сила сопротивления пропорциональна скорости тела

При больших скоростях пропорциональна квадрату скорости

Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения*

Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила

А сейчас сравним закон гравитации и силу тяжести

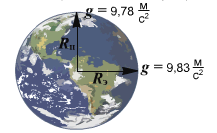
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.

Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.

При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.

Источник

Формула расчета силы реакции опоры

Расчет реакций относится к разделу физики с названием «Статика», которая рассматривает структуру и системы, находящиеся в покое.

Силой реакции опоры называется усилие противодействия опоры действующему на нее объекту, при этом она равна по модулю и противоположна по направлению усилию, с которым объект действует на опору, согласно третьему закону Ньютона.

Система между некоторой структурой и опорой, которая препятствует линейному или угловому перемещению этой структуры, называется системой опоры. Существует несколько типов опор:

Расчет равновесных систем связан с вычислением результирующего динамического момента. В ньютоновской (классической) механике момент силы определяется как векторное произведение усилия, действующего на опору, на вектор, образованный между точкой опоры и точкой приложения этого усилия. Момент силы также называют динамическим моментом или просто моментом.

Далее в статье приводится пример расчета реакции для наиболее распространенной задачи: балки с двумя опорами.

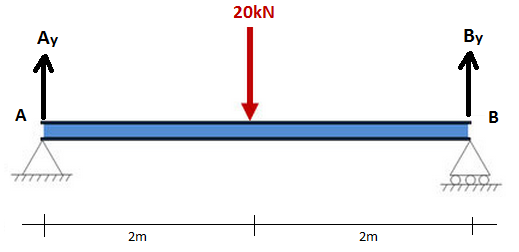
Решение задачи о реакции опоры балки

Как было сказано выше, балка с двумя опорами является типичной и наиболее простой задачей статики. Задача состоит в расчете реакций в точках А и В ввиду действующих на балку усилий.

Знание этих величин необходимо для правильного понимания диаграмм моментов и диаграмм сил данной системы, и является важной частью статики в школьных и университетских курсах. Существует компьютерная программа SkyCiv, которая предоставляет мощный инструмент по расчету таких реакций для различных равновесных систем.

Возвращаясь к поставленной выше задаче, напомним, что основным ее условием является статическое состояние, то есть отсутствие каких-либо линейных перемещений и вращений объектов. В простой физике последний факт означает, что сумма векторов всех усилий равна нулю (то есть сумма усилий, направленных вверх, равна таковым, направленным вниз). Вторым условием равновесия системы является равенство нулю динамических моментов, приложенных относительно определенной точки опоры.

Чтобы определить реакции подпорок балки, следуйте нижеизложенным двум способам решения задачи:

Первый способ: через моменты

Например, рассчитаем сумму всех динамических моментов относительно точки реакции В, учитывая ее равенство нулю в равновесии. Выбор точки В, относительно которой будет проводиться расчет, является произвольным, точно так же можно выбрать точку А. Таким образом, просуммируем все динамические моменты относительно точки В, полагая эту сумму равной нулю:

Отметим, что в формуле выше мы выбрали положительное направление для моментов, действующих против часовой стрелки, и отрицательное направление для моментов, действующих по часовой стрелке. Такой выбор знаков моментом является наиболее общим, однако, вы можете выбрать и наоборот. Необходимо помнить, что всегда нужно использовать одно и то же соглашение на знак моментов, начиная сначала и следуя ему на протяжении всего решения конкретной задачи.

Таким образом, мы получили нашу первую формулу, из которой определили силу реакции опоры в точке А. Аналогичная формула запишется для определения реакции в точке В. В нашем случае, ввиду симметричности действующего вертикально вниз усилия в 20 кН относительно точек подпорок, реакция в точке В будет равна таковой в точке А, то есть 10 кН.

Второй способ: через силы

Для существования равновесия сумма всех вертикальных сил должна быть равна нулю, то есть ΣF y = 0, где индекс Y определяет конкретную вертикальную силу в системе. Помните, что в данном случае мы должны включать в расчет все действующие в системе силы. Принимая во внимание последний факт, проводим суммирование всех вертикальных сил, в итоге получаем следующую формулу:

Так же, как и в случае моментов сил, силы являются векторными величинами и имеют знак, здесь мы приняли за положительные силы те, которые действуют вверх, и за отрицательные те, которые действуют вниз. Выбор знака остается за вами, однако, напоминаем, что этот выбор не должен изменяться в процессе решения задачи. Отметим, что в формуле выше мы использовали результат, полученный в предыдущем пункте, когда вычислили силу реакции Ay.

Таким образом, мы решили, поставленную в начале этого параграфа задачу о расчете сил реакций опоры балки, используя при этом две системы уравнений, уравнения момента силы и уравнения силы, и получили ответы: силы реакции в точках А и В равны между собой и составляют 10 кН. Напоминаем, что физический смысл полученного равенства заключается в том, что действующая на балку внешняя сила приложена точно посередине балки. В случае ее приложения в другой точке, приведенные формулы также будут действительны и процесс расчета остается тем же самым.

Видео

Эта видеоподборка поможет вам лучше разобраться в теме и закрепить полученные знания.

Источник