практические приложения уравнения бернулли
Некоторые практические приложения уравнения Бернулли
Рассмотрим применение уравнения Бернулли для определения скоростей и расходов и времени истечения жидкостей из резервуаров.
Принципы измерения скорости и расхода жидкости. Для определения скоростей и расходов жидкостей в промышленной практике обычно применяются дроссельные приборы и пневмометрические трубки.
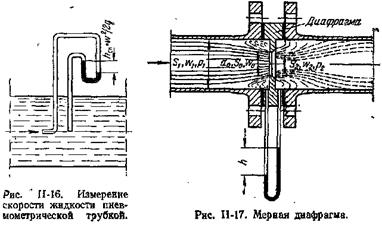
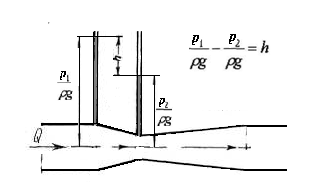
Принцип работы пневмометрических трубок, например трубки Пито-Прандтля, может быть пояснен с помощью рис. II-16. В каждом сечении разность уровней жидкости в трубках, изображенных на рисунке, выражает скоростной напор hск в точке сечения, лежащей на оси трубы.
Разность уровней рабочей жидкости в трубках удобнее измерять не посредством пьезометрических трубок, как показано на рис. II-16, а при помощи дифференциального манометра (рис. II-17). Его U-образная трубка заполнена жидкостью, которая не смешивается с рабочей и имеет значительно большую плотность, чем последняя (например, вода или спирт – при работе с газами или ртуть – при работе с капельными жидкостями). Это позволяет измерять перепады давлений в случае значительного избыточного давления (или вакуума) в трубопроводе при относительно небольшой высоте прибора.
По результатам измерений 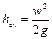
Такой способ определения скорости и расхода жидкости прост, но недостаточно точен из-за трудности установки пневмометрических трубок строго вдоль оси трубопровода.

В качестве дроссельных приборов используют мерные диафрагмы, сопла и трубы Вентури.
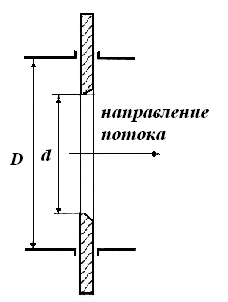
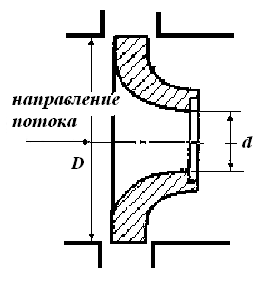
Мерная диафрагма (рис. II-17) представляет собой тонкий диск с отверстием круглого сечения, центр которого расположен на оси трубы. Мерное сопло (рис. II-18) является насадкой, имеющим плавно закругленный вход и цилиндрический выход. Дифманометры мерных сопел (а также диафрагм) присоединяют к трубопроводу через кольцевые камеры а, соединенные с внутренним пространством трубопровода отверстиями, равномерно расположенными по окружности, или двумя каналами b.




Коэффициент a называется коэффициентом расхода дроссельного прибора. Его значение зависит от значения критерия Рейнольдса для жидкости и от отношения диаметра отверстия дроссельного прибора к диаметру трубопровода:
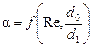
Значения a, определенные опытным путем, приводятся в специальной и справочной литературе.
Диаметр дроссельного устройства обычно в 3-4 раза меньше диаметра трубопровода, поэтому величиной (d2/d1) 2 в уравнении (II,54) можно в первом приближении пренебречь и находить расход жидкости по уравнению
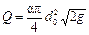
Среднюю скорость жидкости в трубопроводе определяют, разделив Q на площадь сечения трубопровода. Опуская индексы «1» у w1 и d1, получим
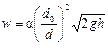
В случае работы со сжимаемыми жидкостями (газом или паром) при больших перепадах давлений в уравнения (II,56) и (II,57) вводят еще один поправочный коэффициент, учитывающий изменение плотности газа (пара).
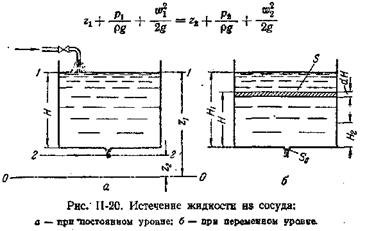
Истечение жидкостей. Определим расход жидкости при ее истечении через круглое отверстие в тонком днище открытого сосуда, в котором поддерживается постоянный уровень H жидкости (рис. II-20, а).
Вытекающая из такого отверстия струя резко сжимается при выходе вследствие инерционного движения частиц жидкости, приближающихся внутри сосуда к отверстию по криволинейным траекториям (некоторые из них даже непосредственно перед выходом еще скользят почти параллельно днищу, то есть перпендикулярно оси струи). Расстояние от днища до сжатого сечения (вслед за которым дальнейшее сужение струи из-за увеличения скорости падающей жидкости выражено гораздо слабее) невелико и составляет около половины диаметра отверстия.
Выбрав плоскость сравнения 0—0 параллельной днищу сосуда, напишем уравнение Бернулли (считая жидкость идеальной) для сечения 1—1, соответствующего верхнему уровню жидкости в сосуде, и сечения 2—2, плоскость которого проходит через указанное сжатое сечение вытекающей струи:
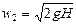
что соответствует известной формуле Торричелли.
При движении реальной жидкости часть напора H теряется на трение и преодоление сопротивления, обусловленного внезапным сужением потока в отверстии. Поэтому скорость реальной жидкости в сжатом сечении:
где j — поправочный коэффициент (j 3 /сек) жидкости равен произведению ее скорости w2 на площадь сжатого сечения S2 струи. Обозначим отношение S2 площади поперечного сечения S0 отверстия в днище через e. Это отношение e = S2/S0 называют коэффициентом сжатия струи.
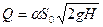
Коэффициент a представляет собой коэффициент расхода и выражается произведением коэффициентов скорости и сжатия струи:
Этот коэффициент определяют опытным путем, его значения зависят от значения критерия Re и могут быть найдены в справочниках в зависимости от свойств и скорости жидкости, а также от формы отверстия, его размера и удаленности от стенок сосуда.
Из уравнения (II,59) следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты постоянного уровня жидкости над отверстием и от размера отверстия, но не зависит от формы сосуда. Это уравнение применимо также для определения расхода жидкости, вытекающей через отверстие в тонкой боковой стенке сосуда, если считать Н расстоянием от верхнего уровня жидкости до оси отверстия.
Для жидкостей, по вязкости мало отличающихся от воды, можно принимать в первом приближении ее a » 0.62. При истечении жидкости через короткий цилиндрический патрубок (насадок) происходит дополнительная потеря напора на входе и выходе жидкости, что приводит к снижению j. Вместе с тем струя при входе в патрубок после некоторого сжатия снова расширяется и вытекает, заполняя все его сечение, т.е. можно считать e = I. В итоге коэффициент расхода жидкости при истечении через насадок оказывается большим, чем при истечении через отверстие, и для воды может быть принят a » 0.82.
Если сосуд, из которого вытекает жидкость, закрыт и давление р2 над жидкостью в нем отличается от наружного давления р1, то при определении расхода по формуле (II,59) вместо H в нее следует подставить 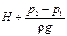
Теперь рассмотрим истечение при переменном уровне жидкости в сосуде с целью определения времени опорожнения сосудов.
При таком истечении жидкости (рис. II-20,б) ее уровень H в сосуде снижается во времени и, согласно уравнению (II,58), уменьшается также скорость истечения w0. Следовательно, процесс истечения носит нестационарный характер.
Определим время, за которое уровень жидкости в сосуде опустится от первоначальной высоты H1 до некоторой высоты H2. За бесконечно малый промежуток времени dt., в соответствии с уравнением (II,59), через отверстие в днище вытечет объем жидкости
dV = Qdt = aS0
где S0 — площадь поперечного сечения отверстия в днище сосуда.
За тот же промежуток времени dt уровень жидкости в сосуде понизится на бесконечно малую величину dH, и при постоянной площади поперечного сечения S сосуда убыль жидкости в нем составит
Знак минус в правой части указывает на уменьшение высоты жидкости в сосуде.
Приравнивая, согласно уравнению неразрывности потока, эти объемы, получим
aS0 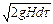
Проинтегрируем это выражение, принимая, что коэффициент расхода a постоянен, т.е. не зависит от скорости истечения:
Таким образом, время опорожнения сосуда, имеющего постоянно поперечное сечение, от высоты H1 до высоты H2 составляет
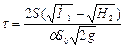
В случае полного опорожнения резервуара H2 = 0 и уравнение (II,61) принимает вид
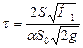
Решая задачу о времени опорожнения сосуда, площадь поперечного сечения которого изменяется по высоте (например, при истечении из конических резервуаров, горизонтальных цистерн и т.п.), следует при интегрировании выражения dt. учесть зависимость площади сечения S от уровня Н жидкости, т.е. учесть вид функции S = f(H).
Практическое применение уравнения Бернулли (измерение расхода жидкости с помощью дроссельных расходомеров)



При применении уравнения Бернулли для решения практических задач гидравлики следует помнить два основных условия:
1) уравнение Бернулли может быть применено только для тех живых сечений потока, в которых соблюдаются условия плавно изменяющегося движения.
2) гидродинамическое давление р и, следовательно, высоту положения z можно относить к любой точке живого сечения, так как 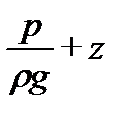
Разберем применение уравнения Бернулли на примере измерения скорости и расхода жидкости в трубопроводе.
В практической деятельности используются различные способы измерения расхода жидкостей, однако, наибольшее распространение в настоящее время получили нормальные дроссельные расходомеры. Под термином «нормальные» следует понимать объединенные государственными нормалями геометрически подобные, как бы стандартные устройства.
К нормальным дроссельных расходомерам относятся диафрагмы, сопла и трубы Вентури (рисунок 23 а-в) [11,12].
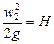
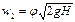
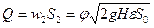
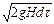
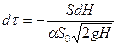
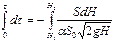
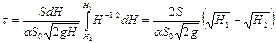



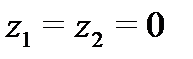 , примем α1 = α2=…=1.
, примем α1 = α2=…=1.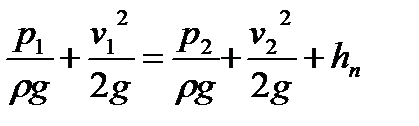 или
или 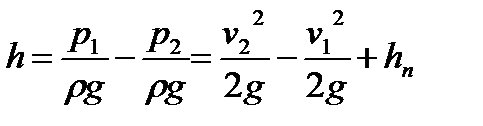
 – потери напора между сечениями 1–1 и 2–2,
– потери напора между сечениями 1–1 и 2–2,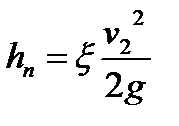 ,
, =
=  , получим
, получим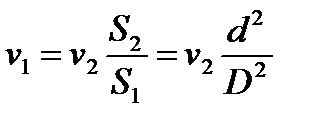 ,
,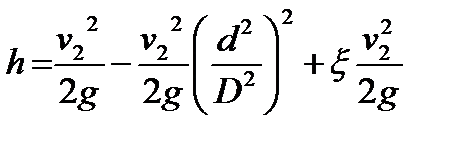 ,
,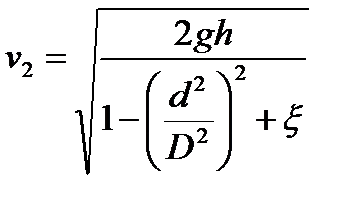 ,
,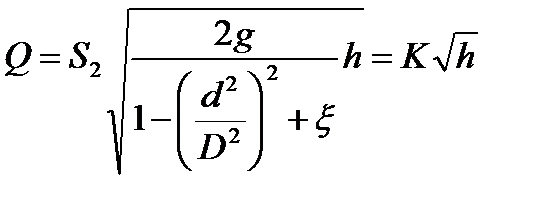
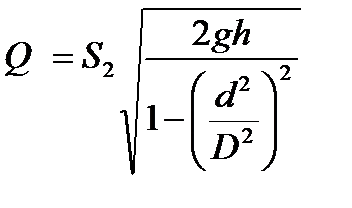
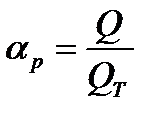 ,
,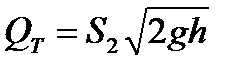 , для идеальной жидкости получаем:
, для идеальной жидкости получаем: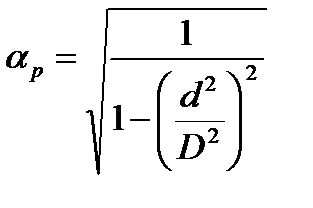 ,
,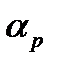 для реальной жидкости зависит также от критерия Рейнольдса, то есть:
для реальной жидкости зависит также от критерия Рейнольдса, то есть: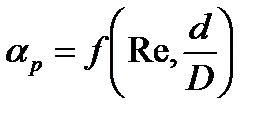 .
.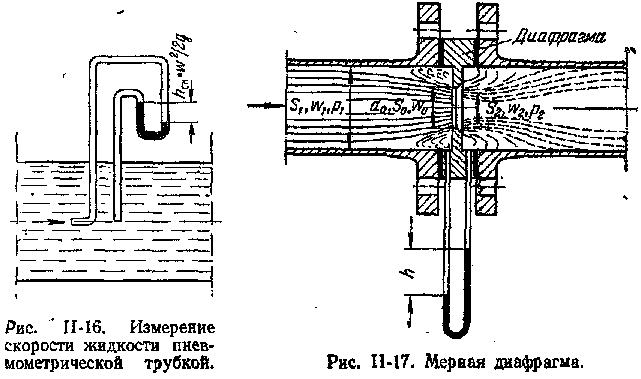
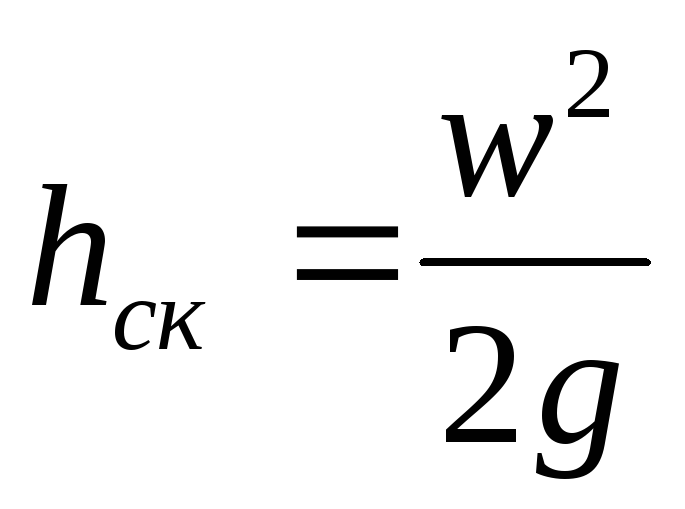 находят максимальную скорость жидкости вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода (рис.II-10), передвигая пневмометрическую трубку в различные точки сечения, либо используют соотношения между средней и максимальной скоростями при ламинарном и турбулентном режимах течения. Расход жидкости находят, умножая среднюю скорость на площадь поперечного сечения трубопровода.
находят максимальную скорость жидкости вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода (рис.II-10), передвигая пневмометрическую трубку в различные точки сечения, либо используют соотношения между средней и максимальной скоростями при ламинарном и турбулентном режимах течения. Расход жидкости находят, умножая среднюю скорость на площадь поперечного сечения трубопровода.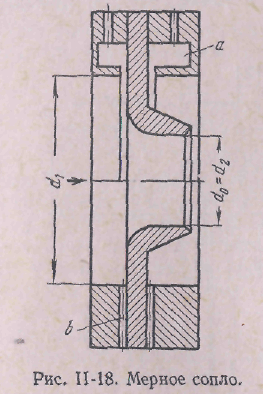 олее широко распространено определение скоростей и расходов жидкостей с помощьюдроссельных приборов, принцип работы которых основан на измерении перепада давлений при изменении поперечного сечения трубопровода. При искусственном сужении сечения потока посредством дроссельного прибора скорость и, соответственно, кинетическая энергия потока в этом более узком сечении возрастают, что приводит к уменьшению потенциальной энергии давления в том же сечении. Поэтому, измерив дифференциальным манометром перепад давлений между сечением трубопровода до его сужения и сечением в самом сужении (или вблизи него), можно вычислить изменение скорости между сечениями, а по нему — скорость и расход жидкости.
олее широко распространено определение скоростей и расходов жидкостей с помощьюдроссельных приборов, принцип работы которых основан на измерении перепада давлений при изменении поперечного сечения трубопровода. При искусственном сужении сечения потока посредством дроссельного прибора скорость и, соответственно, кинетическая энергия потока в этом более узком сечении возрастают, что приводит к уменьшению потенциальной энергии давления в том же сечении. Поэтому, измерив дифференциальным манометром перепад давлений между сечением трубопровода до его сужения и сечением в самом сужении (или вблизи него), можно вычислить изменение скорости между сечениями, а по нему — скорость и расход жидкости.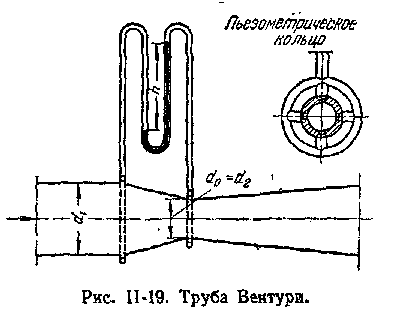
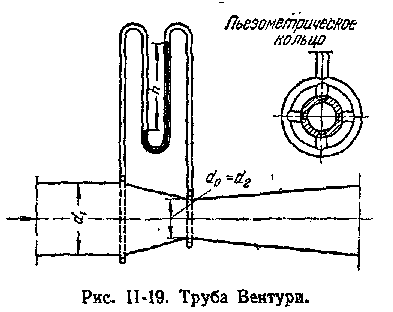
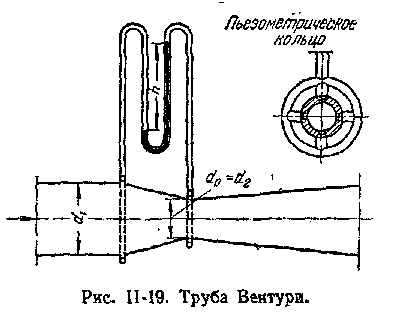
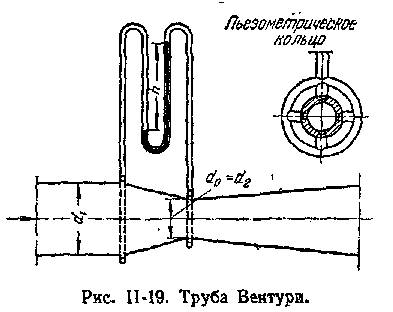 руба Вентури (рис. II-19) имеет постепенно сужающееся сечение, которое затем расширяется до первоначального размера. Вследствие такой формы трубы Вентури потеря давления в ней меньше, чем в диафрагмах или соплах. Вместе с тем длина трубы Вентури очень велика по сравнению с толщиной диафрагмы или сопла, которые могут быть установлены между фланцами трубопровода.
руба Вентури (рис. II-19) имеет постепенно сужающееся сечение, которое затем расширяется до первоначального размера. Вследствие такой формы трубы Вентури потеря давления в ней меньше, чем в диафрагмах или соплах. Вместе с тем длина трубы Вентури очень велика по сравнению с толщиной диафрагмы или сопла, которые могут быть установлены между фланцами трубопровода.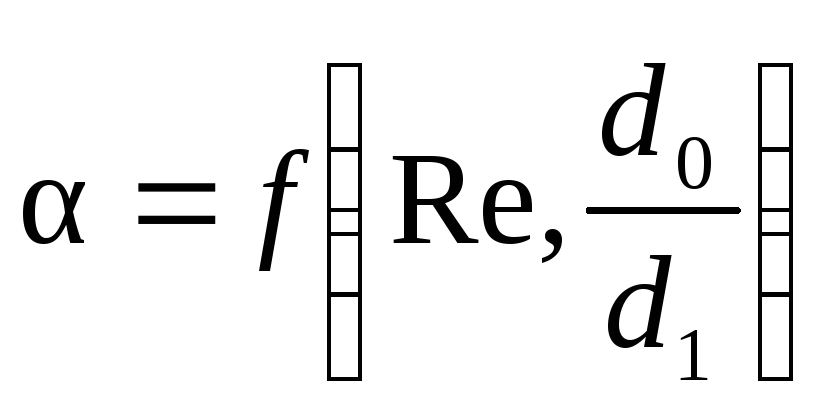 (II,55)
(II,55)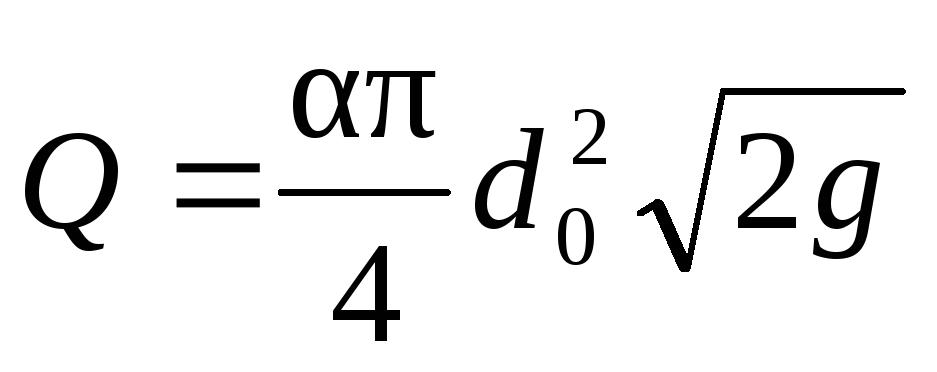 (II,56)
(II,56)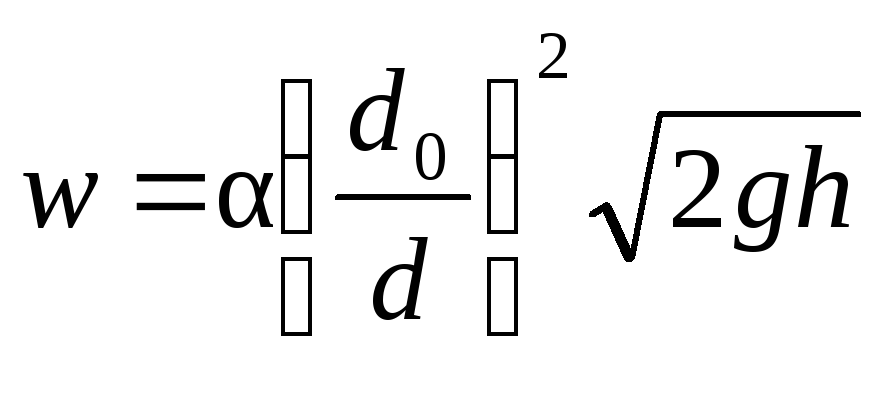 (II,57)
(II,57)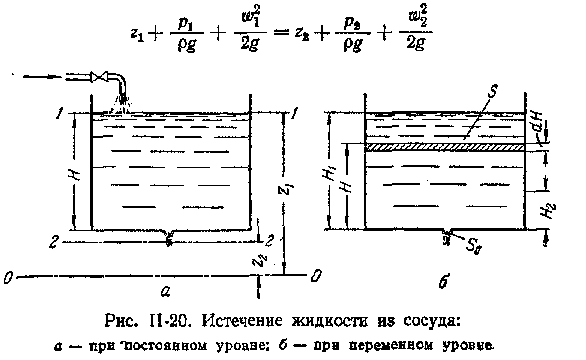
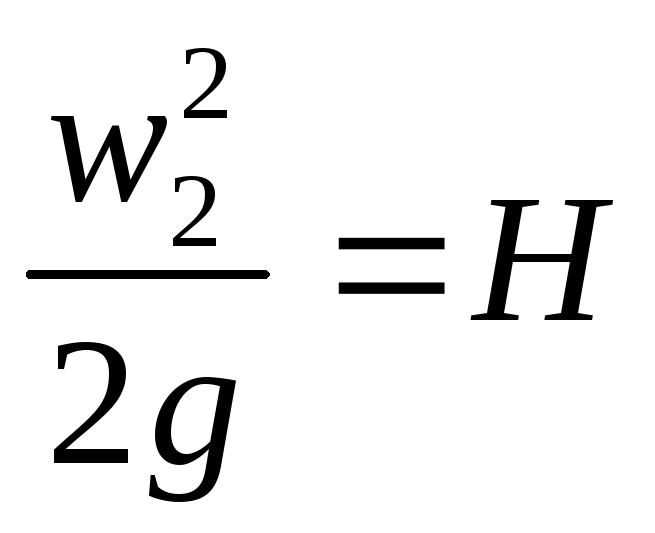
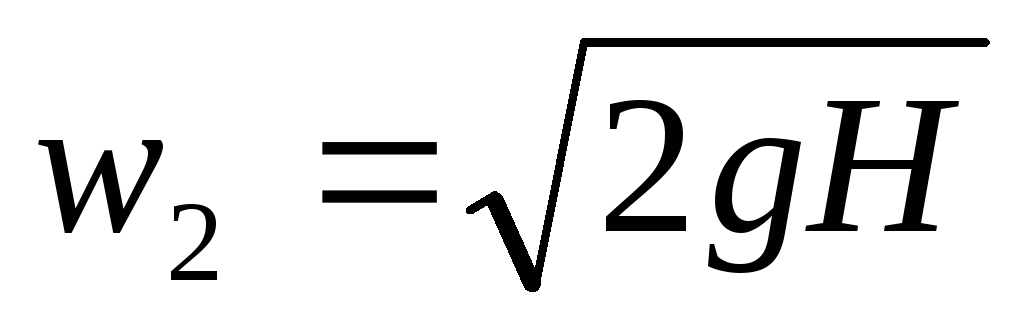 (II,58)
(II,58)
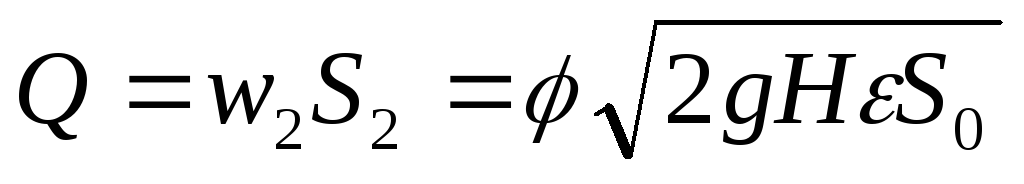
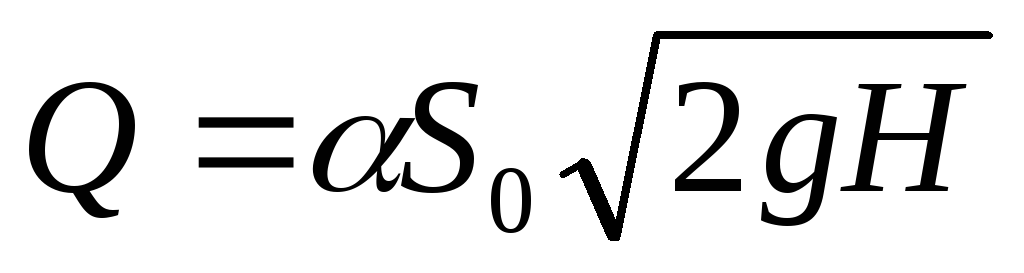 (II,59)
(II,59)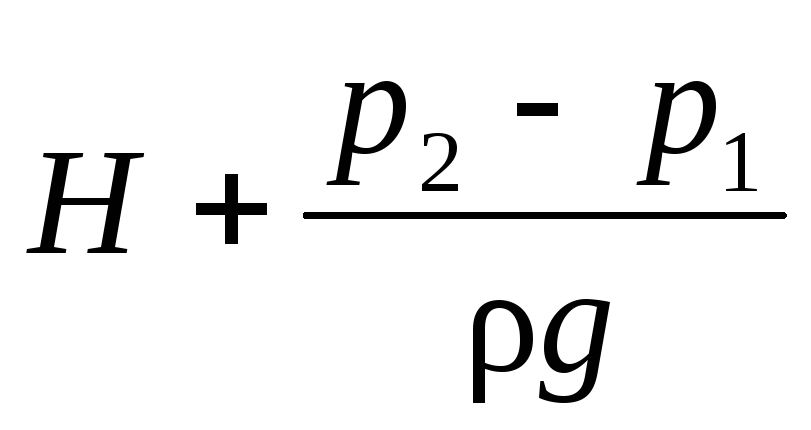 , где — плотность жидкости.
, где — плотность жидкости.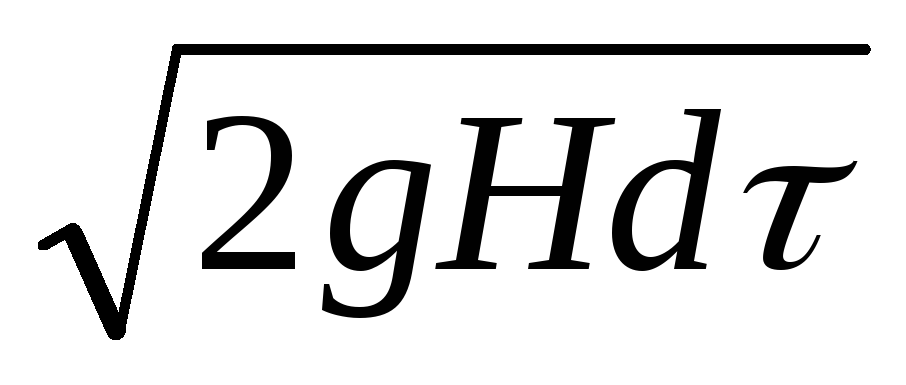
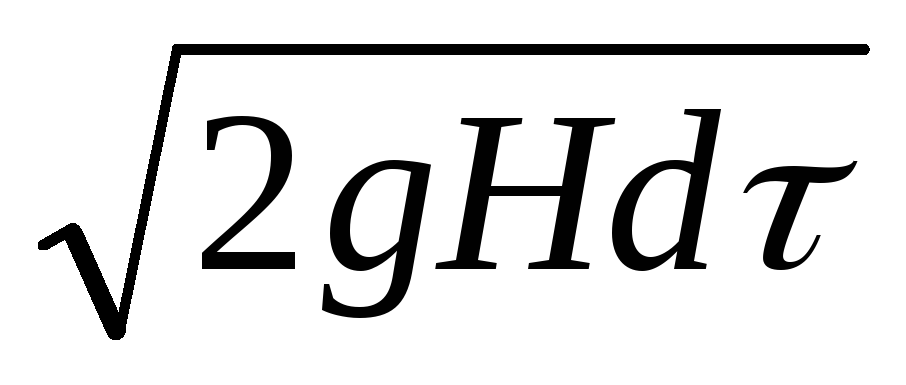 =— SdH
=— SdH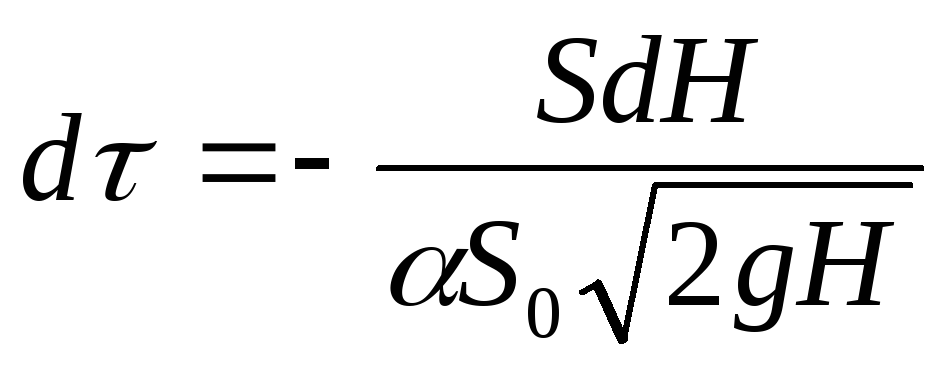
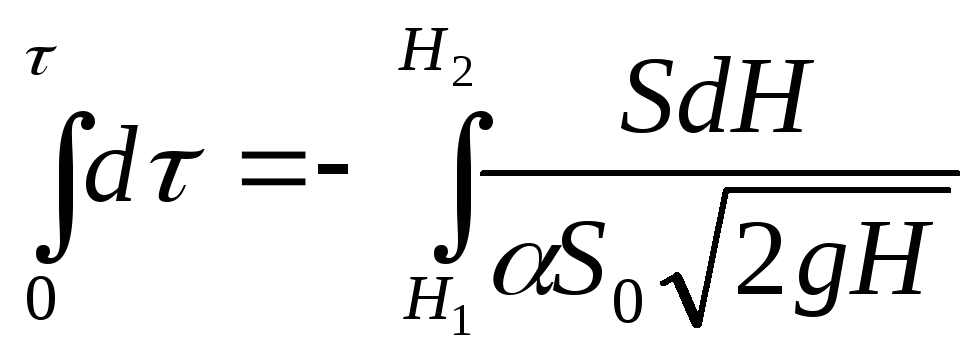
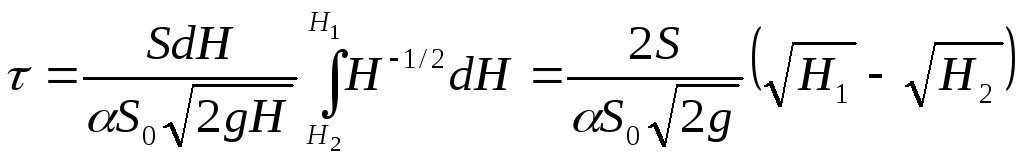
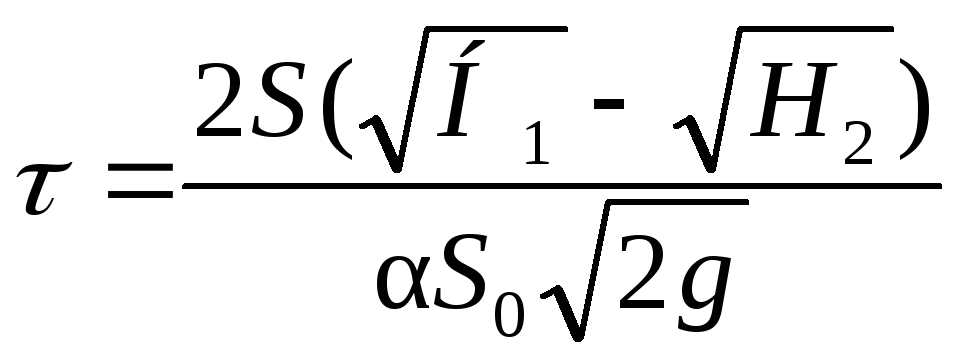 (II,61)
(II,61)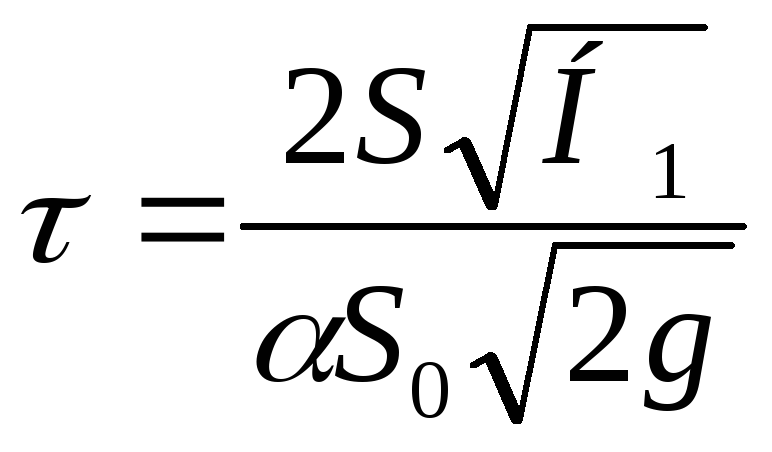 (II,61а)
(II,61а)