практические приложения подобия треугольников 8 класс

Класс: 8

Презентации к уроку

Цели и задачи урока:

Ход урока

Слайды 1-2 (Презентация 1)

Геометрия всегда решала те задачи, которые перед ней ставила жизнь. Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие детские игрушки подобны предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, две фотографии разного формата.

Мы уже знаем, что в геометрии фигуры одинаковой формы принято называть подобными. Сегодня мы обсудим, как свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности.

Для начала в этом нам помогут герои известного мультфильма «Шрек».

Начнем мы со сказки День Рождения Шрека или Практическое применение подобия треугольников. (Презентация 2)

Слайд 3 (Презентация 1)

Уже в XVI в. В России нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

Слайд 4 (Презентация 1) Вот один пример.Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнемуконцужезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Дляудобства расчетов и измерений жезл был разделен на 1000 равных частей.

Рассмотрим несколько случаев из истории и литературы.

1. Определение высоты предмета по длине его тени.

Слайд 5-7 (Презентация 1)

Греческие ученые решили множество практических задач, которые до них люди не умели решать. Например, за шесть веков до нашей эры греческий мудрец Фалес Милетский научил египтян определять высоту пирамиды по длине ее тени.

Как это было, рассказывается в книге Я.И. Перельмана «Занимательная геометрия».Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени.

Слайд 8 (Презентация 1)

Я хочу прочитать вам эту маленькую притчу.

«Усталый северный чужеземец пришел в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона и что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.

— Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

Слайд 9-11 (Презентация 1)

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Он измерил тень от палки и тень от пирамиды. Сравнивая соотношения высот реальных предметов с длинами их теней, Фалес нашел высоту пирамиды.

Определение высоты пирамиды по длине ее тени.

АВС подобен D СDE (по двум углам):

ВСА= СED=90°;

АВС= СDЕ, т. к. соответственные при АВ || DС и секущей АС (солнечные лучи падают параллельно)

В подобных треугольниках сходственные стороны пропорциональны:

.

Таким образом, Фалес нашел высоту пирамиды.

Вопрос классу: Однако, способ предложенный Фалесом, применим не всегда. Почему?

2. Определение высоты предмета по шесту.

Слайд 12-15 (Презентация 1)

При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, которыйживописнопредставлен у Жюль Верна в известном романе «Таинственный остров».

Читаем отрывок из романа.

— Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.

Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

Взяв прямой шест, длиной 10 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки.

Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком.

— Помнишь свойства подобных треугольников?

— Их сходственные стороны пропорциональны.

— Да, и, следовательно, если мы измерим два расстояния, то зная высоту шеста, сможем вычислить четвёртый неизвестный член пропорции, т.е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты.

Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.

По окончании измерений инженер составил следующую запись:

Н 333,33

Значит, высота гранитной стены равнялась приблизительно 333 футам».

Преимущества способа Жюль Верна:

— можно производить измерения в любую погоду;

3. Определение высоты предмета.

Есть несколько простых способов определения высоты предметов. Например, такие способы приведены в настольной книге охотника-спортсмена.

Слайд 16 (Презентация 1)

По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.

Слайд 17-18 (Презентация 1)

Вместо лужицы можно пользоваться положенным горизонтально зеркальцем. Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека.

АВD подобен D EFD (по двум углам):

ВАD = FED=90°;

АDВ = EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны:

; .

Таким образом, найдена высота объекта.

4. Определение расстояния до недоступного объекта.

Рассмотрим применение подобия треугольников к определению расстояния до недоступного объекта. Слайд 19-25 (Презентация 1, с использованием Приложения 1).

5. Практическое задание. Слайд 26 (Презентация 1)

Предлагается решить задачу № 583.В ней предлагается, применив подобие треугольников, измерить ширину реки.Чертеж к задаче имеется в учебнике. Ученикам необходимо объяснить, как получен такой чертеж, доказать подобие треугольников и провести вычисления.

По построению АВС подобен АВ₁С₁ (по двум углам).

В подобных треугольниках сходственные стороны пропорциональны:

;;;

6. Рассмотрение и обсуждение примеров. Слайды 27-28 (Презентация 1).

7. Дополнительный материал. Слайд 29-30 (Презентация 1 с использованием Приложения 1)

8. Подведение итогов.

Домашнее задание: пункт 64 параграфа 3, стр. 150-151, № 581, 582, придумать свои задачи на определение высоты предмета и определение расстояния до недоступной точки (оформить либо в виде презентации, либо в виде практической работы в формате А4).

Источник

Урок «Практические приложения подобия треугольников», 8 класс.

Выбранный для просмотра документ Приложение 1.pptx

Описание презентации по отдельным слайдам:

Карта путешествия Б Н П

Какие типы практических задач можно решить, применяя подобие треугольников? Какие инструменты или подручные средства можно использовать? Пусть Муза Геометрии будет к Вам всегда благосклонна.

Практические приложения подобия треугольников Цель урока: повторить признаки подобия треугольников выяснить, какие знания геометрии могут быть полезны человеку в окружающем мире научиться применять признаки подобия треугольников для решения практических задач

Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида. Преимущества: не требуются вычисления. Недостатки: нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени. Способ Фалеса

Жюль Верн «Таинственный остров»

Объясните по рисунку: как герои романа Жюля Верна определили высоту скалы. А С В Е F FE = 10 футов, FB = 15 футов BC = 500 футов

Домашнее задание Повышенный уровень: Какая минимальная высота должна быть у плоского зеркала, чтобы вы могли увидеть себя в нем в полный рост? Творческий уровень: придумать задачу практического содержания и подготовить ее презентацию Базовый уровень: Человек, стоя на краю ручья, видит в 3м перед собой отражение вершины столба, высотой 9м, который стоит на другом берегу ручья. Расстояние от земли до уровня глаз человека равно 1м 50см. Найдите расстояние от человека до столба. Ответ дайте в метрах.

сегодня я узнал… было интересно… было трудно… я выполнял задания… я понял, что… теперь я могу… я приобрел… я научился… у меня получилось … я смог… я попробую… меня удивило… урок дал мне для жизни… Подведем итоги Одним предложением, выбирая начало фразы из предложенного списка, подведите итог нашего урока.

Что получалось? Над чем надо ещё работать? Что надо повторить? Оцените свою работу на уроке.

Выбранный для просмотра документ Приложение 2.docx

Приключения Вити Перестукина в древнем Египте

Витя и его болтливый кот, Кузька, бодро шагали по лесной тропинке. За беспечным разговором они не заметили, как лес остался позади, а под ногами появился песок. Вокруг простиралась пустыня … Такой пейзаж напоминал мальчику Египет. Похожую картинку он видел на странице в учебнике.

В ожидании новых приключений, Витя зашагал вперед, а следом за ним трусцой побежал кот, ворча и жалуясь на жару. Вдруг перед ними словно из-под земли вырос огромный замок с широкими каменными стенами и высокими башнями. За всем величием этого построения Витя не заметил покалеченных людей вокруг него и чей-то плач, доносившийся сверху. Неожиданно чья-то тяжелая рука опустилась на плечо мальчика. Он обернулся и застыл от ужаса… Это был воин.

-Кто ты, мальчик?- спросил незнакомец.

Витька уже собрался было ответить но, вспомнив предыдущие приключения, решил соврать.

— Да я тут так…мимо проходил.

-Тогда помоги нам. Этот мальчишка неправильно решил задачу. Он неверно подсчитал высоту крепости и подобрал лестницу, по которой должны были спуститься мои воины. Этот двоечник выбрал слишком короткую лестницу, и многие люди покалечились.

Ребята, а вы знаете, как начертить фронтальный вид крепости? Как определять углы с помощью ладони?

Помогите Виктору Перестукину выпутаться из этой неприятной истории.

Источник

Презентация к уроку геометрии (8 класс) по теме «Практические приложения подобия треугольников»

Описание презентации по отдельным слайдам:

Уменьшает страх, повышает настроение Ощущение свежести и покоя, снимает головные боли Снижение нервного утомления, давления, коррекция зрения Стимулирование творчества

Практические приложения подобия треугольников. О подобии произвольных фигур 26.02.15 Классная работа

ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ЗАДАЧА №1

А С В А1 О С1 ОВ1 = 4 см Найти ВО и ВВ1 ОВ1 = 4 см (1 часть) 8 4 ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ЗАДАЧА №2

ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ЗАДАЧА №3

А В В1 С С1 Определить ширину реки ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ЗАДАЧА №4

B C А D Задача 5 16 9 20 15 12 Найдите неизвестные линейные элементы прямоугольного треугольника АВС. ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОДОБИЯ ТРЕУГОЛЬНИКОВ

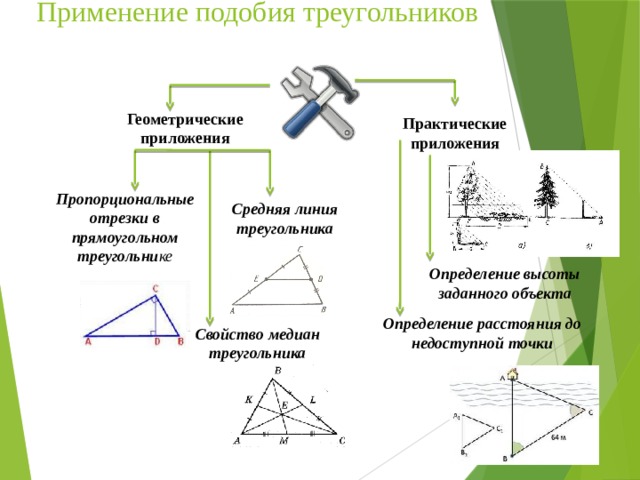
Применение подобия треугольников Геометрические приложения Практические приложения Средняя линия треугольника Пропорциональные отрезки в прямоугольном треугольнике Определение высоты заданного объекта Определение расстояния до недоступной точки Свойство медиан треугольника

Взаимопроверка «5», если 14 и более баллов «4», если 9-13 баллов «3», если 5-8 баллов Номер вопроса Верный ответ Количество баллов за верный ответ 1 да 1 б 2 да 1 б 3 да 1 б 4 нет 1 б 5 нет 1 б 6 нет 2 б 7 да 2 б 8 нет 2 б 9 да 3 б 10 да 3 б

Всё ли в природе можно измерить? Возможно ли измерить недоступное?

Источник

Практические приложения подобия треугольников

Содержимое разработки

Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх того, и умения.

Практические приложения подобия треугольников .

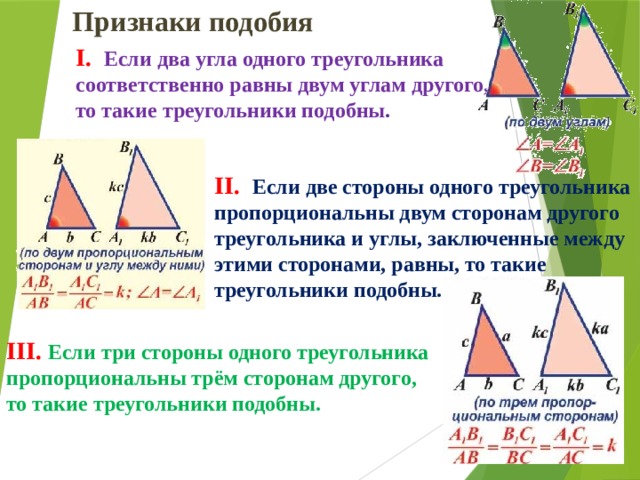
I. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны .

II. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

III. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

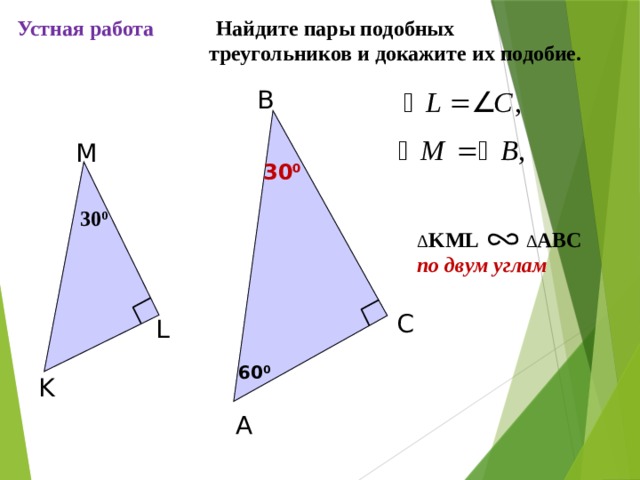
Найдите пары подобных треугольников и докажите их подобие.

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

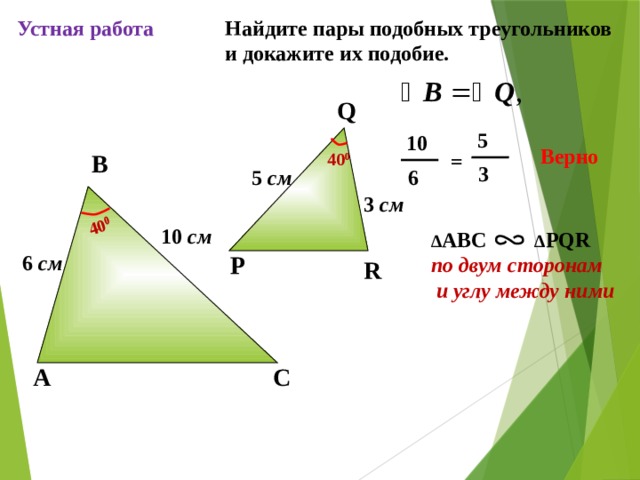
Найдите пары подобных треугольников и докажите их подобие.

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

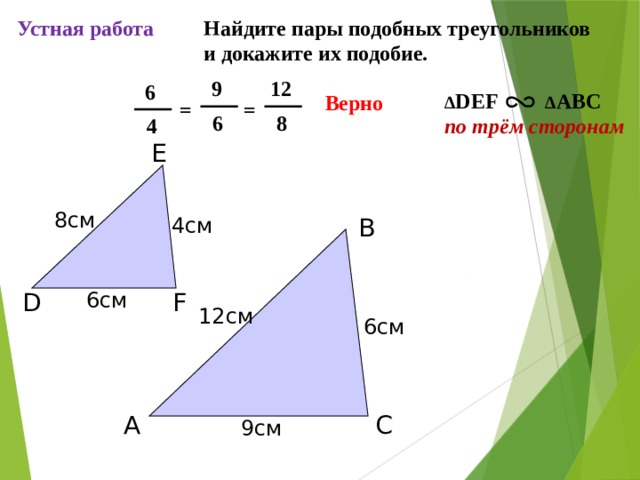
Найдите пары подобных треугольников и докажите их подобие.

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

Применение подобия треугольников

Пропорциональные отрезки в прямоугольном треугольни ке

Средняя линия треугольника

Определение высоты заданного объекта

Определение расстояния до недоступной точки

Свойство медиан треугольника

Если высказывание истинно – отвечаем “Да”, если ложно – “Нет”

Источник

Урок геометрии по теме «Практические приложения подобия треугольников». 8-й класс

Разделы: Математика

Класс: 8

Тема урока: Практические приложения подобия треугольников.

Тип урока: Урок закрепления знаний.

Перед тем как приступить к изучению нового материала, повторим самые известные в геометрии теоремы, которые вы изучали совсем недавно. Это теорема Пифагора и обратная ей. (Презентация. На экране Слайд 1).

Примерные ответы учащихся:

Для того, чтобы узнать тему нашего сегодняшнего урока, вам придётся немного потрудиться. А поможет вам в этом как раз теорема, обратная теореме Пифагора.

Торопись, ведь дни проходят,
Мы у времени в гостях.
Не рассчитывай на помощь,
Помни: все в твоих руках!

Перед вами лежат карточки (Приложение 1), на них изображены треугольники. Для каждого треугольника определите, является он прямоугольным или нет. Если не является, то соответствующую букву вычеркните. Из оставшихся букв составьте слово – оно и является символом темы сегодняшнего урока. (Слайд 2)

Учащиеся работают в парах, все вычисления выполняют на черновиках.

Итак, все буквы найдены, У меня к вам вопрос: Какое же слово у вас получилось? (Подобие.) (Слайд 3) А тема нашего урока “Практические приложения подобия треугольников”.

А теперь запишите в тетрадях число и тему урока “Практические приложения подобия треугольников”.

Давайте определимся с тем, какие цели мы поставим перед собой при изучении данной темы. (Слайд 4)

Первую поставленную цель мы уже достигли – повторили теорему Пифагора и обратную ей теорему, с их помощью выяснили тему урока.

Затем, раз уж мы с вами будем говорить о подобии треугольников, надо повторить признаки подобия треугольников.

Потом я расскажу вам, как на практике применяется подобие треугольников.

И, наконец, вы сами сможете воспользоваться признаками подобия треугольников при решении задач.

Перейдём к выполнению второй поставленной задачи: повторим признаки подобия треугольников. Сформулируйте, пожалуйста, признаки подобия треугольников.

Примерные ответы учащихся: (ответы появляются на экране по мере их поступления). (Слайд 5)

Теперь я попрошу вас рассказать друг другу эти признаки, чтобы закрепить их основательно.

Учащиеся работают в парах, рассказывают друг другу признаки.

Проверим сейчас, как вы усвоили применение признаков при решении простейших задач. Для этого вам надо ответить на вопросы теста, выбрать правильные ответы. Карточки с вопросами перед вами. (Приложение 2).

Учащиеся отвечают на вопросы.

Проверим, каким образом вы справились с поставленной задачей. Попрошу выйти к доске с тетрадями пять человек. На экране будут появляться правильные ответы. (Слайд 6) Если ваш ответ верен, то стоим на месте, если же вы ошиблись, то делаем шаг назад. Кто в итоге останется на месте, заработает отметку “5”, и так по убывающей.

Учащиеся выполняют проверку.

Учитель оглашает отметки.

Итак, мы с вами повторили всё, что необходимо знать для практического применения признаков подобия треугольников. Теперь поставлю перед вами задачу, которую я, как учитель именно математики, решила легко, а у других это вызывает затруднения. Итак, однажды, около одного из домов в нашей деревне мы с ребятами увидели одиноко стоящее дерево, ель. (Слайд 7)

Возник вопрос: а не упадёт ли эта ель на дом, не разрушит ли его. Конечно, расстояние от дома до дерева известно, а вот высота ели – нет. Как же быть? Ответить на вопрос помогла одна из трёх вещей, которые сейчас и перед вами. Это верёвка, зеркало и книга Жюля Верна “Таинственный остров”. (Слайд 8) Попробуйте догадаться, чем воспользовалась я?

Учащиеся предлагают свои варианты.

Помогла мне книга. Открываем главу 15…(Слайд 9–10) Здесь подробно рассказано, как вычислить высоту отвесной стены. (На слайде текст один из учащихся зачитывает его вслух.)

Попробуем воспроизвести действия профессора. И сделаем рисунки и записи в тетради.

Один из учащихся встаёт около окна с ёлкой в руках(изображая ель), второй встаёт между дверью и окном посередине, третий ложится на коврик у двери. С помощью рулетки измеряем расстояние от ели до шеста(от первого до второго) и от шеста до глаз лежащего ученика. Всю картинку видим на слайде. (Слайд 11–12)

Учащиеся выполняют записи и рисунки в тетради.

Учитель выполняет рисунки и записи на доске.

Ну а теперь по данным чертежа составим пропорцию. (Слайд 13)

Учащиеся делают необходимые записи в тетради.

Используя выводы нашего исследования, решим задачу на вычисление высоты ракеты, если известна длина её тени. Соответствующий рисунок перед вами на карточках. (Приложение 3). (Слайд 14)

Решение проведём на доске все вместе, составив соответствующую пропорцию.

Выполним проверку по заранее приготовленному решению на экране. (Слайд 15)

А теперь проверим, сможете ли вы самостоятельно применить полученные сегодня знания. Для этого вам надо решить задачу, её условие на экране. (Слайд 16)

Учащиеся решают задачу.

Если вы уже справились с решением, то проверьте свои результаты с тем, как дело обстоит на самом деле.

Итак, давайте вспомним, о чём мы вели речь на сегодняшнем уроке?

Примерные ответы учащихся:

Давайте посмотрим, выполнили ли мы с вами поставленные цели? (Слайд 17)

Мы повторили теорему Пифагора и обратную ей теорему? (Да.)

Мы повторили признаки подобия треугольников? (Да.)

Мы познакомились с одним из способов применения подобия на практике? (Да.)

Мы узнали кое – что новое и интересное? (Да.)

Значит, поставленные цели выполнены? (Да.)

Значит, урок прошёл не зря? (Да.)

Запишите, пожалуйста, домашнее задание. № 580, № 579. При решении этих задач вам пригодятся те практические навыки работы, с которыми познакомились сегодня. (Слайд 18)

Итак, урок закончен, всем спасибо за работу.

Источник