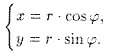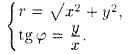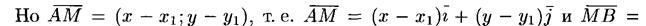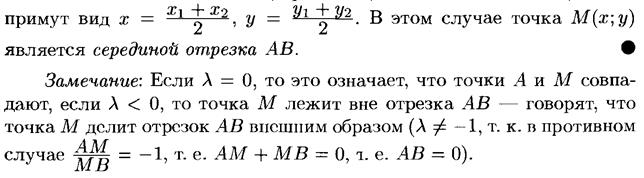основные приложения метода координат на плоскости

Система координат на плоскости

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем являетсяпрямоугольная (декартова) система координат.

Единичные векторы осей обозначают i и j(| i |=| j |=1, 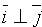). Систему координат обозначают Оху, а плоскость, в которой расположена

система координат, называют координатной плоскостью.

Рассмотрим произвольную точку Μ плоскости Оху. Вектор ОМ называется радиусом-вектором точки М.

Координатами точки Μ в системе координат Оху называ­ются координаты радиуса-вектора OM. Если OM=(x;y), то координаты точки Μ записывают так: М(х;у), число xназывается абсциссой точки М, у — ординатой точки Μ.

Эти два числа x и y полностью определяют положение точки на плоскости, а именно: каждой паре чисел x и y соответствует единственная точка М плоскости, и наоборот.

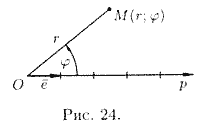
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, на­зываемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором e того же направления, что и луч Ор.

Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием г от полюса О и углом φ, образован­ным отрезком ОМ с полярной осью (отсчет углов ведет­ся в направлении, противоположном движению часовой стрелки) (см. рис. 24).

Числа r и φ называются полярными координатами точки М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом.

Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (—π; π] (или 0

Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами

Источник

П.4.3. Основные приложения метода координат на плоскости

Эта формула известна из школы.

Замечание.Вывод этой формулы при помощи векторной алгебры – см. лекцию №4, стр.33. (Крищенко А.П…..)

, то есть

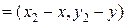
Тогда, векторное уравнение можно записать в координатной форме:

Полученные формулы называются формулами деления отрезка в данном отношении. В частности, при , то есть, если АМ=МВ, то формулы

4.3. Вычисление площадей и объемов

(см. стр. 34-35 электронной лекц. №4 Крищенко А.П.)

Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.

Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется пло­щадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.

Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3;-1;2). Найти его площадь.

Решение.

х =

Модуль этого векторного произведения равен

. Следовательно, .

Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить мо­дуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах . Таким образом, объем этой пирамиды равен V_SABC =

,

Линии на плоскости

Одну и ту же линию на плоскости можно задать разными способами: 1) уравнением в прямоугольных координатах;

2) уравнением в полярных координатах;

3) параметрическими уравнениями;

4) векторным уравнением.

Векторное уравнение линии.

В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти её уравнение.

Вторая: зная уравнение кривой, изучить её форму и свойства.

Примеры некоторых кривых.

1) Окружность.

Циклоида.

3)

Построение линий с помощью сервиса .

Кривые, заданные в полярной системе координат :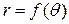

.

Кривые, заданные в полярной системе координат , :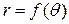

.

Кривые, заданные параметрически :

.

Кривые, заданные параметрически , :

.

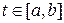
Область, заданную неравенствами вида :

.

Пример.Построить график кривой в полярной системе координат:

.

Составляем запрос на построение графика кривой

Сервис строит кривую на отрезке :

Сервис строит кривую на отрезке :

■

Источник

§ 9. Система координат на плоскости

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат .

Единичные векторы осей обозначают i и j (| i |=| j |=1, ). Систему координат обозначают Оху, а плоскость, в которой расположена

Рассмотрим произвольную точку Μ плоскости Оху. Вектор ОМ называется радиусом- вектором точки М.

Эти два числа x и y полностью определяют положение точки на плоскости, а именно: каждой паре чисел x и y соответствует единственная точка М плоскости, и наоборот.

Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, на­зываемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором e того же направления, что и луч Ор.

Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием г от полюса О и углом φ, образован­ным отрезком ОМ с полярной осью (отсчет углов ведет­ся в направлении, противоположном движению часовой стрелки) (см. рис. 24).

Числа r и φ называются полярными координатами точки М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом.

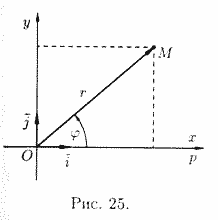
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть x и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты.

Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:

Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами

9.2. Основные приложения метода координат на плоскости

Расстояние между двумя точками

Решение : Искомое расстояние d равно длине вектора , т.е.

Деление отрезка в данном отношении

Требуется разделить отрезок АВ, соединяющий точки A(x₁ ;y₁ ) и В(х₂ ;y₂ ) в заданном отношении λ > 0, т.е. найти координаты точки М(х;у) отрезка АВ такой, что (см. рис. 26).

Решение : Введем в рассмотрение векторы и . Точка Μ делит отрезок АВ в отношении λ, если

(9.1)

Но , т. е. и , т. е. .

Уравнение (9.1) принимает вид

Учитывая, что равные векторы имеют равные координаты, получаем

Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении . В частности, при λ = 1, т.е. если AM = MB, то они примут вид

, . В этом случае точка М(х;у) является серединой отрезка АВ.

Замечание: Если λ = 0, то это означает, что точки A и Μ совпадают, если λ , т. к. в противном случае

, т. е. AM + MB = 0, т. е. АВ = 0).

Требуется найти площадь треугольника ABC с вершинами А(x₁ ;y₁ ), В(х₂ ,y₂ ), С(x₃ ;y₃ ).

Решение: Опустим из вершин А, В, С пер­пендикуляры АА₁ , ВВ₁ , СС₁ на ось Ох (см. рис. 27).

Замечание: Если при вычислении площади треугольника получим S = 0, то это означает, что точки А, В, С лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.

9.3. Преобразование системы координат.

Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.

Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.

Параллельный перенос осей координат

Пусть на плоскости задана прямоугольная система координат Оху. Под параллельным переносом осей координат понимают переход от систе­мы координат Оху к новой системе О₁х ₁у ₁ , при котором меняется поло­жение начала координат, а направление осей и масштаб остаются неиз­менными.

Пусть начало новой системы координат точка О₁ имеет координаты (х₀ ;y₀ ) в старой системе координат Оху, т. е. О₁ (х₀ ;y₀ ). Обозначим координаты произвольной точки Μ плоскости в системе Оху через (х;у), а в новой системе O₁x₁y₁ через (х’;у’) (см. рис. 28).

Полученные формулы позволяют находить старые координаты x и у по известным новым х’ и у’ и наоборот.

Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.

Пусть новая система O₁x₁y₁ получена поворотом системы Оху на угол α.

Пусть Μ произвольная точка плоскости, (х;у) — ее координаты в старой системе и (х’;у’) — в новой системе.

Введем две полярные системы координат с общим полюсом О и полярными осями Ох и Οx₁ (масштаб одинаков). Полярный радиус r в обеих системах одинаков, а полярные углы соответственно равны α + j и φ, где φ — полярный угол в новой полярной системе.

По формулам перехода от полярных координат к прямоугольным имеем

Но rcosj = х’ и rsinφ = у’. Поэтому

Полученные формулы называются формулами поворота осей . Они позволяют определять старые координаты (х; у) произвольной точки Μ через новые координаты (х’;у’) этой же точки М, и наоборот.

Если новая система координат O₁x₁y₁ получена из старой Оху путем параллельного переноса осей координат и последующим поворотом осей на угол α (см. рис. 30), то путем введения вспомогательной системы легко получить формулы

выражающие старые координаты х и у произвольной точки через ее новые координаты х’ и у’.

Источник

Лекция на тему: МЕТОД КООРДИНАТ

1. Д екартовы координаты на прямой

2. Декартовы полярные координаты на плоскости

3. Полярные координаты на плоскости

4. Простейшие задачи на плоскости

5. Линии и их уравнения .

1. Д екартовы координаты на прямой

Аналитическая геометрия есть область математики, изучающая свойства геометрических объектов при помощи метода, в основу которого положено понятие координат.

Ввести координаты на прямой – это значит установить взаимно однозначное соответствие между множеством точек прямой и множеством действительных чисел. Для этого проведем на плоскости горизонтальную прямую. Выберем на ней положительное направление, указываемое стрелкой, точку отсчета О и единицу масштаба (рис. 1).

Таким образом при помощи декартовой системы координат на прямой устанавливается взаимно однозначное соответствие между множеством всех точек прямой и множеством всех действительных чисел: любой точке прямой соответствует определенное действительное число, а любому действительному числу – определенная точка на прямой.

2 . Декартовы и полярные координаты на плоскости

Ввести координаты на плоскости – это значит установить взаимно однозначное соответствие между множеством точек плоскости и множеством упорядоченных пар действительных чисел.

Точку М с полярными координатами r и обозначают символом М ( r ; ). Полярный угол измеряется в радианах. Полюсу О соответствует полярный радиус r = 0, полярный угол для него не определен.

Для того чтобы соответствие между отличными от полюса точками плоскости и упорядоченными парами полярных координат ( r ; ) было взаимно однозначным, обычно считают, что r и изменяются в следующих границах:

Пусть точка М имеет декартовы координаты ( х ; у ) и полярные координаты ( r ; ). Из рис. 5 очевидно, что

В заключение отметим, что иногда на плоскости вводят и другие координаты. Примером могут служить эллиптические координаты – им соответствуют взаимно перпендикулярные семейства эллипсов и гипербол. Такие координаты оказываются удобными при рассмотрении некоторых конкретных задач механики и физики. Однако, в большинстве случаев пользуются самыми простыми координатами – декартовыми прямоугольными координатами.

3. Простейшие задачи на плоскости

1. Р а с с т о я н и е м е ж д у д в у м я т о ч к а м и. Найдем расстояние d между двумя данными точками М ₁ ( х ₁ ; у ₁ ) и М ₂ ( х ₂ ; у ₂ ) (рис. 6). Из прямоугольного треугольника М ₁ NМ ₂ по теореме Пифагора имеем:

О п р е д е л е н и е. Число

Совершенно аналогично вычисляется координата у :

Соотношения (1.9), (1.10) имеют смысл при любых значениях –1. Они называются формулами деления отрезка в данном отношении . Очевидно, если = 1, то точка М делит отрезок пополам. Получающиеся при этом формулы

называются формулами деления отрезка пополам.

Неотрицательную площадь треугольника М ₁ М ₂ М ₃ выразим через площади соответствующих трапеций:

Раскрыв скобки и приведя подобные члены, получим

4. Линии и их уравнения

1. Л и н и я к а к г е о м е т р и ч е с к о е м е с т о т о ч е к. В аналитической геометрии линии рассматриваются как геометрические места точек, их составляющих. Например, окружность определяется как геометрическое место точек плоскости, равноотстоящих от некоторой фиксированной точки плоскости (центра окружности). Биссектрису плоского угла можно рассматривать как геометрическое место точек, равноотстоящих от сторон этого угла, и т. д.

2. П о н я т и е о б у р а в н е н и и л и н и и. Сущность метода координат на плоскости заключается в том, что всякой плоской линии сопоставляется ее уравнение, а затем свойства этой линии изучаются путем аналитического исследования соответствующего уравнения.

Задача о нахождении точек пересечения двух линий, имеющих уравнения F ( х ; у ) = 0 и Ф( х ; у ) = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:

Если эта система не имеет действительных решений, то линии не пересекаются.

3. П а р а м е т р и ч е с к о е п р е д с т а в л е н и е л и н и и. Для аналитического представления линии L часто бывает удобно выражать текущие координаты х и у точек этой линии при помощи третьей вспомогательной переменной ( параметра ) t двумя уравнениями вида

Разумеется, роль параметра t могут играть также некоторый угол, длина дуги или другая неименованная переменная.

Заметим, что для исключения параметра t из уравнений (1.16) достаточно возвести в квадрат и сложить эти уравнения. С учетом тождества мы получим при этом уравнение окружности вида (1.13):

З а м е ч а н и е. Часто линию L определяют не уравнением (1.13), а разрешенным (например, относительно у ) уравнением

где, согласно формулам (1.5), введено обозначение

будут алгебраическими. Степени их соответственно равны 1, 2, 5.

Общий вид алгебраического уравнения первой степени :

Общий вид алгебраического уравнения второй степени :

Всякая неалгебраическая линия называется трансцендентной.

В дальнейшем курсе аналитической геометрии мы будем изучать алгебраические линии первого и второго порядков, определяемые уравнениями (1.21) и (1.22). В связи с аналитическим представлением линии этими уравнениями возникают задачи двух типов :

по заданным геометрическим свойствам линии составить ее уравнение ;

Источник