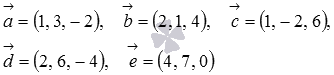Как определить что векторы компланарны

Компланарные векторы и условие компланарности

В данной статье мы рассмотрим такие темы, как:

Определение компланарных векторов

Компланарные векторы — это векторы, которые параллельны одной плоскости или лежат на одной плоскости.

Два любых вектора всегда компланарны, поскольку всегда можно найти плоскости параллельные 2-м произвольным векторам.

Условия компланарности векторов

Примеры решения задач на компланарность векторов

Исследуем на компланарность векторы

Как решить?

Векторы будут являться компланарными, если их смешанное произведение равно нулю, поэтому вычисляем смешанное произведение заданных векторов. Для этого составляем определитель, по строкам которого записываются координаты векторов-сомножителей:

Отсюда следует, что смешанное произведение не равняется нулю, поэтому векторы не являются компланарными.

Ответ: векторы не являются компланарными.

Докажем, что три вектора

Как решить?

Находим смешанное произведение данных векторов:

Из данного примера видно, что смешанное произведение равняется нулю.

Ответ: векторы являются компланарными.

Проверим, компланарны ли векторы

Как решить?

Необходимо найти количество линейно независимых векторов: записываем значения векторов в матрицу и выполняем элементарные преобразования:

Из 2-ой строки вычитаем 1-ю, из 4-ой вычитаем 1-ю, умноженную на 3:

К 3-ей строке прибавляем 2-ю:

Поскольку в матрице только две ненулевые строки, делаем вывод, что среди них всего два линейно независимых вектора.

Ответ: векторы являются компланарными, поскольку среди них всего два линейно независимых вектора.

Источник

Компланарность векторов. Условия компланарности векторов.

рис. 1

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Условия компланарности векторов

Примеры задач на компланарность векторов

Решение: найдем смешанное произведение векторов

Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.

Решение: найдем смешанное произведение векторов

Ответ: вектора компланарны так, как их смешанное произведение равно нулю.

Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования

	1	1	1
	1	2	0
	0	-1	1
	3	3	3

из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3

111111

к 3-тей строке добавим 2-рую

111

Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.

Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.

Источник

Какие векторы называют компланарными

Компланарные векторы – это векторы, которые лежат в одной плоскости, или параллельны какой-либо плоскости.

Рассмотрим три вектора в трехмерном пространстве. Любые два из них будут компланарными всегда. Поэтому, компланарность проверяют минимум для трех векторов.

Почему любые два вектора всегда компланарны

Поясним факт, что любые два вектора будут компланарными.

Для начала вспомним, какие векторы называют равными. Равны векторы, у которых совпадают три характеристики: длина, направление, соответственные координаты.

При параллельном переносе вектор не поворачивается. Этот новый вектор \( \vec> \) будет иметь те же длину, направление и координаты, что и начальный вектор до сдвига. Другими словами, с помощью параллельного переноса можно получить вектор, равный данному вектору.
\[ \vec = \vec> \]

Если два вектора равны, то вместо одного из них мы сможем использовать второй, когда это будет удобным для нас.

Проделаем теперь те же операции с каким-либо другим вектором \( \vec \). В результате получим вектор \( \vec> \), равный вектору \( \vec \).

Любые два вектора можно параллельным переносом сдвинуть так, чтобы совместить их начальные, или конечные точки. Значит, через эти векторы можно провести пересекающиеся прямые. А такие прямые будут лежать в одной плоскости.

Таким образом, любые два вектора всегда компланарны.

Например, любые два орта Декартовой прямоугольной системы координат компланарны, а тройка ортов – некомпланарные векторы. Подробнее об ортах тут (откроется в новой вкладке).

Условие компланарности

Найдем смешанное произведение трех векторов.

Если такое произведение будет равно нулю, то три вектора компланарные.

Условие компланарности векторов:
\[\large \boxed < \left( \vec, \vec , \vec \right) = 0 >\]

Как вычислить смешанное произведение

Смешанное произведение можно обозначить еще одним способом:

Результат смешанного произведения – это число. Если число равно нулю, то векторы компланарны.

Как применять смешанное произведение

Если три вектора не компланарны, то на них, как на сторонах, можно построить параллелепипед, или пирамиду.

С помощью смешанного произведения можно рассчитывать объемы параллелепипедов или треугольных пирамид, построенных на трех некомпланарных векторах.

Примечание:
Определитель может быть равен отрицательному числу. А объем может быть либо нулевым, либо положительным. Поэтому, если при вычислении объема определитель будет равен отрицательному числу, знак минус не учитываем.

Рисунок 2 поясняет, как с помощью векторов на ребрах параллелепипеда можно рассчитать его объем

Рисунок 3 поясняет, как с помощью векторов на ребрах пирамиды можно рассчитать ее объем

Смешанное произведение векторов в физике — работа вращающей силы

Пусть цилиндрическое тело вращается под действием силы. Ось вращения проходит через ось симметрии тела.

Работа вращающей силы – это смешанное произведение векторов \( \vec <\omega>\), \(\vec < r>\) и \(\vec < F>\)

\[ \large \boxed < dA = \left( \vec\left[ \vec <\omega>, \vec \right] \right)\cdot dt >\]

Пояснения:

Линейная скорость – это векторное произведение радиуса окружности на угловую скорость:

Расстояние, \( \vec\) которое проходит точка при повороте на небольшой угол — – это произведение вектора линейной скорости на скалярную величину – время:
\[ \vec = v \cdot dt \]

Небольшая работа dA – это скалярное произведение вектора силы на вектор перемещения
\[ dA = \left( \vec \cdot \vec \right)\]

Источник

Компланарные векторы, исследование системы векторов на компланарность.

В этой статье мы поговорим о компланарности векторов. Сначала вспомним определение компланарности и получим необходимое и достаточное условие компланарности трех векторов в трехмерном пространстве. Далее разберемся с задачей исследования системы из n векторов на компланарность, рассмотрим решения характерных примеров.

Навигация по странице.

Необходимое и достаточное условие компланарности трех векторов.

Напомним определение компланарных векторов.

Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.

А как же определить, являются ли три вектора компланарными?

Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.

Для компланарности трех векторов и трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Пусть , докажем что векторы и компланарны.

Так как , то векторы и перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор перпендикулярен и вектору и вектору . Следовательно, векторы и компланарны, так как перпендикулярны одному вектору .

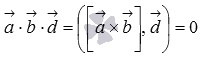
Пусть теперь векторы и компланарны, докажем равенство нулю смешанного произведения .

Так как векторы и компланарны, то вектор перпендикулярен каждому из них, следовательно, скалярное произведение вектора на равно нулю, что означает равенство нулю смешанного произведения .

Итак, теорема полностью доказана.

Покажем применение доказанного условия компланарности трех векторов к решению задач.

Компланарны ли векторы , заданные в прямоугольной системе координат.

Вычислим их смешанное произведение по координатам:

Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.

Необходимое и достаточное условие компланарности векторов можно использовать для проверки принадлежности четырех точек пространства А, В, С и D одной плоскости. Для этого находим координаты векторов и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.

Принадлежат ли точки 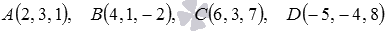одной плоскости?

Найдем координаты векторов (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца):

Теперь вычисляем смешанное произведение этих векторов

Так как смешанное произведение векторов отлично от нуля, то векторы не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.

Исследование системы векторов на компланарность, примеры и решения.

А как же быть, если требуется установить компланарность системы векторов, число векторов которой больше трех?

Давайте ответим на этот вопрос и получим условие компланарности системы из n векторов трехмерного пространства.

В предыдущем пункте мы показали, что для компланарности трех векторов и необходимо и достаточно равенство нулю их смешанного произведения: . Так как смешанное произведение трех векторов в координатной форме представляет собой определитель матрицы, строками которой являются координаты векторов и , то условие компланарности можно записать в виде . Вспомнив понятие ранга матрицы, последнее равенство можно интерпретировать следующим образом: ранг матрицы, строками которой являются координаты компланарных векторов и , меньше трех.

Обобщив последнее утверждение, мы получим необходимое и достаточное условие компланарности системы из n векторов трехмерного пространства: для компланарности системы из n векторов трехмерного пространства необходимо и достаточно, чтобы ранг матрицы, строками которой являются координаты векторов системы, был меньше трех.

Компланарны ли векторы

Составим матрицу, строками которой примем координаты данных векторов

Сразу легко отыскать минор второго порядка, отличный от нуля, .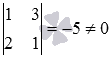

Переберем окаймляющие его миноры третьего порядка:

Все они равны нулю, следовательно, ранг матрицы равен двум, поэтому, векторы заданной системы векторов компланарны в силу выполнения необходимого и достаточного условия компланарности.

Источник

Компланарность векторов. Условия компланарности векторов.

Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.

Условия компланарности векторов

Примеры задач на компланарность векторов

Решение: найдем смешанное произведение векторов

Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.

Решение: найдем смешанное произведение векторов

Ответ: вектора компланарны так, как их смешанное произведение равно нулю.

Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования

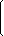	1	1	1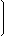
	1	2	0
	0	-1	1
	3	3	3

из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3

к 3-тей строке добавим 2-рую

Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.

Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.

Источник