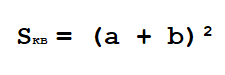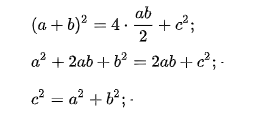что вам нужно для теоремы пифагора
Теорема Пифагора: история, формулы и доказательства
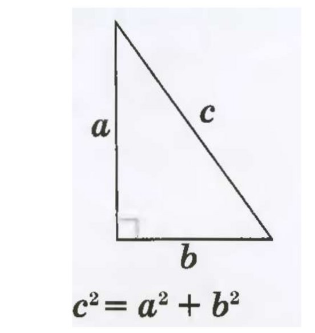
Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.
Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.
После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.
О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.
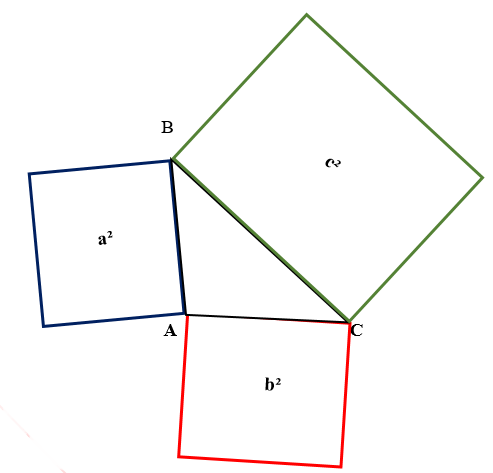
В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пусть ВС = а; АС = b; АВ = с.
Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:
Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:
А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему «Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора».
Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.
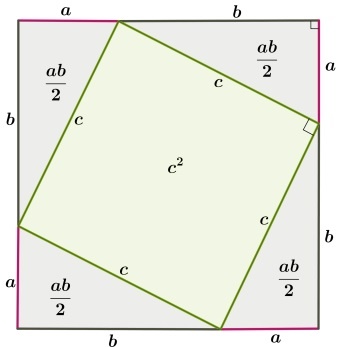
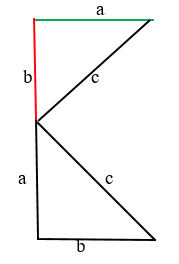
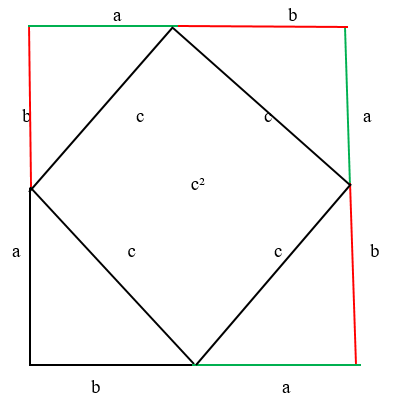
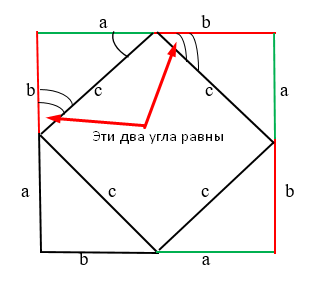
Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.
Площадь этого квадрата можно будет найти благодаря формуле:
Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:
Итак, теорема Пифагора доказана.
2. Доказательство Евклида
Доказательство Евклида также называется «Пифагоровы штаны». Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.
На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.
В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе «Учебники по геометрии за 8 класс».
Пример задачи на применение теоремы Пифагора
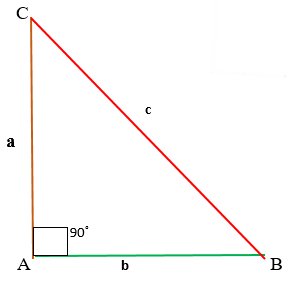
Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.
Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:
АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.
Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу «ГДЗ и решебники по геометрии за 8 класс».
А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе «Онлайн уроки за 8 класс по геометрии». Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.
Доказательства теоремы Пифагора
Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.
Теорема Пифагора — краткая история
Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.
Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формулировка теоремы
Изначальная (геометрическая) формулировка Пифагора гласила:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Позднее появился алгебраический вариант:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.
Уравнение
В виде формулы теорема Пифагора записывается следующим образом:
Доказательство через подобные треугольники
Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.
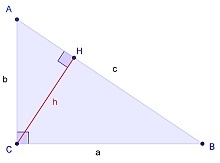
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:
CB 2 =ABxHB, AC 2 =ABxAH
Сложив между собой квадраты катетов, получаем:
AC 2 +CB 2 =ABx(HB+AH)=AB 2
Это и требовалось доказать.
Другие способы доказательства теоремы
Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.
Методом площадей
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.
Площадь внешнего квадрата включает в себя:
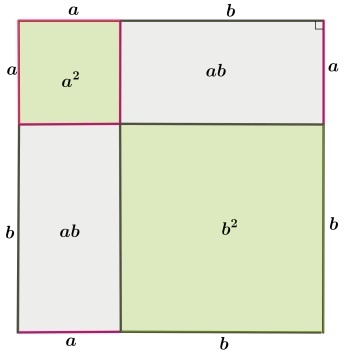
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.
Методом бесконечных малых
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.
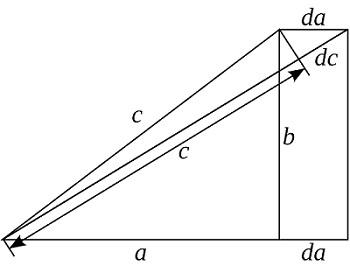
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем
Разделяя переменные составляется дифференциальное уравнение:
Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:
определяя из начальных условий константу интегрирования, получим:
a = 0 ⇒ c 2 = b 2 = const
Таким образом мы определяем, что
Следствие из теоремы Пифагора
Его так же называют обратной теоремой Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
В алгебраическом виде это можно представить так:
c2=a2+b2, где:
Применение теоремы
Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.
Расстояние между точками
Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:
Евклидова метрика
В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:
Теория чисел
Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.
Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.
Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.
Примеры решения задач
Задача 1
В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.
Решение
Для нахождения ответа подставим в формулу исходные значения:
Задача 2
Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.
Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:
Задача 3.
Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.
Решение
Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.
Теорема Пифагора
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Вы узнаете, как доказать теорему, формула Пифагора и как решать задачи.
История теоремы
Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.
Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.
Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.
Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Теорема Пифагора, формула
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы (
). Это одна из основополагающих теорем эвклидовой геометрии.
Формула:
Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.
То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны – . Это и есть геометрическое объяснение Пифагора.
Доказательство теоремы методом площадей: 1 способ
Докажем, что .
Рассмотрим всё тот же треугольник с катетами a, b и гипотенузой c.
Получается такой же треугольник, только перевёрнутый.
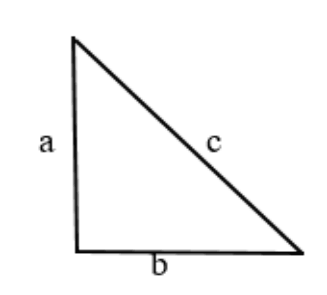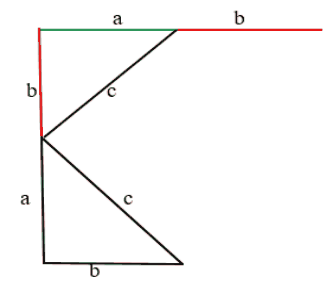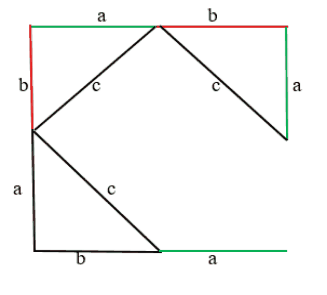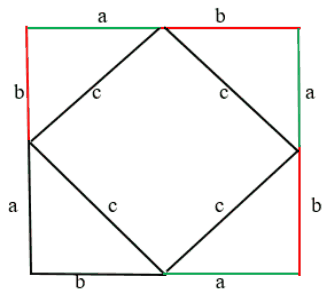
Аналогично строим и с другой стороны: от катета “а” проводим линию катета “b” и вниз “а” и “b” А снизу от катета “b” проводим линию катета “а”. В центре от каждого катета провели гипотенузы “с”. Таким образом гипотенузы образовали квадрат в центре.
Этот квадрат состоит из 4-х одинаковых треугольников. А площадь каждого прямоугольного треугольника = половина произведения его катетов. Соответственно, . А площадь квадрата в центре =
, так как все 4 гипотенузы со стороной
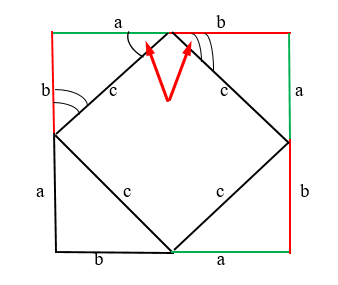
. Стороны четырёхугольника равны, а углы прямые. Как нам доказать, что углы прямые? Очень просто. Возьмём всё тот же квадрат:
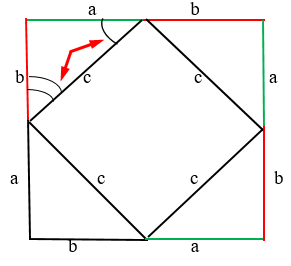
Мы знаем, что эти два угла, показаны на рисунке, являются 90 градусам. Так как треугольники равны, значит следующий угол катета “b” равен предыдущему катету “b”:
Сумма этих двух углов = 90 градусов. Соответственно, предыдущий угол тоже 90 градусов. Конечно же, аналогично и с другой стороны. Соответственно, у нас действительно квадрат с прямыми углами.
Так как острые углы прямоугольного треугольника в общей сложности равняются 90 градусам, то угол четырёхугольника так же будет равен 90 градусов, ведь 3 угла в сумме = 180 градусов.
Соответственно, площадь квадрата складывается из четырёх площадей одинаковых прямоугольных треугольников и площади квадрата, который образован гипотенузами.
Таким образом, получили квадрат со стороной . Мы знаем, что площадь квадрата со стороной
– это будет квадрат его стороны. То есть
. Этот квадрат состоит из четырёх одинаковых треугольников.
И это значит, что мы доказали теорему Пифагора.
ВАЖНО. Если находим гипотенузу, тогда складываем два катета, а затем ответ выводим из корня. При нахождении одного из катетов: из квадрата длины второго катета вычитаем квадрат длины гипотенузы и находим квадратный корень.
Примеры решения задач
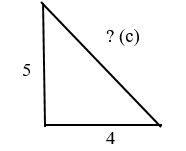
Дано: прямоугольный треугольник с катетами 4 и 5.
Найдите гипотенузу. Пока её обозначим “с”
Сумма квадратов катетов равняется квадрату гипотенузы. В нашем случае –
.
Воспользуемся теоремой Пифагора:
Итак, , а
. Катеты в сумме получают 41.
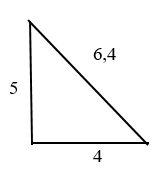
Тогда . То есть квадрат гипотенузы равен 41.
Квадрат числа 41 = 6,4.
Мы нашли гипотенузу.
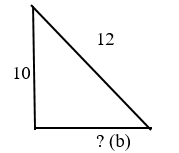
Дано: прямоугольный треугольник, где гипотенуза = 12, один катет = 10
Найдите второй катет.
Обозначим неизвестный катет – b.
Воспользуемся теоремой Пифагора:
, а
Находим
Если , тогда просто
Второй катет (b) равен 6,6.
Заключение
Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.
Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: (это вся теорема Пифагора).