Без проскальзывания что значит физика

10.07.202211.07.2022 admin 0 Comments

Качение без скольжения

Физика > Качение без скольжения

Качение без скольжения можно распределить на вращательное и поступательное движения.

Задача обучения

Основные пункты

Термины

Если с самого начала объект переворачивается без буксирования, то можно говорить о качении без проскальзывания. Чтобы разобраться, давайте рассмотрим пример с колесом на плоской горизонтальной поверхности.

Движение без проскальзывания понять намного проще, если выделить в нем движение центра масс с линейной скоростью v и вращательное движение вокруг центра с угловой скоростью w.

Движение качения отображает комбинацию вращательного и поступательного движений

Когда объект катится по плоскости без скольжения, точка контакта не смещается. Если представим, что колесо движется со скоростью v, то заметно, что оно должно также совершать движение вокруг своей оси с угловой скоростью ω.

Угловая скорость тела (ω) расположена прямо пропорционально скорости движения. Вы ведь могли заметить: чем быстрее разогналась машина, тем больше оборотов совершают колеса. Чтобы вычислить точную связь между линейной и угловой скоростями, можно взять случай, где колесо смещается на дистанцию х при повороте на углу θ.

Тело, скатывающееся на дистанцию х на плоскости, лишенной скольжения

В математике длина дуги приравнивается к углу сегмента, умноженному на радиус объекта (R). Отсюда выходит, что длина дуги колеса, повернутого на θ, достигает Rθ. Так как колесо постоянно контактирует с поверхностью, длина дуги также равна х. Выходит:

Не забывайте, что х и θ зависят от времени, поэтому возьмем их производные:

Здесь аналогичен v в линейной скорости, а – угловой скорости ω. Теперь можно все упростить:

Источник

Учебники

Журнал «Квант»

Общие

§3. Криволинейное движение. Плоскопараллельное движение твердого тела

3.6 Плоскопараллельное движение

Движение твердого тела называется плоскопараллельным, если траектории движения всех его точек являются плоскими кривыми, лежащими в параллельных плоскостях.

Плоскопараллельное движение твердого тела можно представить как суперпозицию поступательного движения и вращения вокруг оси, направление которой не изменяется. Наглядными примерами такого движения являются качение колеса, движение книги без отрыва от стола и т.д.

Для описания положения абсолютно твердого тела при плоскопараллельном движении необходимо задать две декартовые координаты какой-либо точки тела [1] и угол его поворота, то есть плоскопараллельное движение обладает тремя степенями свободы.

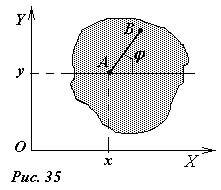
Выберем внутри тела две точки A, B; зададим координаты x_A, y_A точки A и угол φ, который образует отрезок AB с направлением оси X. Три числа x_A, y_A и φ однозначно определяют положение тела на плоскости, следовательно, являются его координатами. Зная эти координаты, можно определить положение в пространстве любой другой точки твердого тела путем геометрических построений.

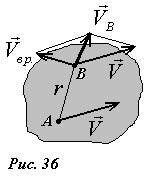
Покажем теперь, как можно найти скорость любой точки твердого тела при плоскопараллельном движении (рис. 36).

причем вектор скорости вращательного движения направлен перпендикулярно отрезку AB и равен по абсолютной величине V_BP = ωr, где r расстояние от точки B до оси вращения.

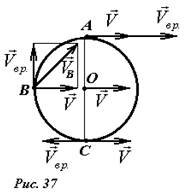
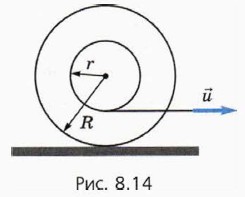
Рассмотрим катящееся без проскальзывания колесо радиуса R (рис. 37).

Пусть его центр движется со скоростью \(

\vec V\). Найдем скорости некоторых других точек колеса. Для этого представим движение колеса как сумму поступательного движения его центра и вращения вокруг его оси. Так как движение происходит без проскальзывания, то угловая скорость вращения определяется формулой \(

\omega = \frac<\upsilon>\). Для точек, находящихся на ободе колеса линейная скорость вращательного движения равна по модулю скорости поступательного движения, так как для них расстояние до оси вращения равно радиусу колеса, поэтому \(

Так как разложение движения на составляющие не является однозначным, можно теперь представить качение колеса как сумму движения точки C и вращения вокруг оси, проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому появляется возможность рассматривать движение колеса как чистый поворот вокруг точки C. Правда, это возможно в течение только бесконечно малого промежутка времени, потому, что в следующий момент точкой касания будет другая точка колеса. Множество точек твердого тела, скорости которых в данный момент равны нулю, образуют мгновенную ось вращения тела. Такая ось существует при любом движении твердого тела. Правда положение этой оси постоянно изменяется, поэтому для вычисления координат точек такое представление движения не дает особых преимуществ. Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как чистый поворот очень удобно.

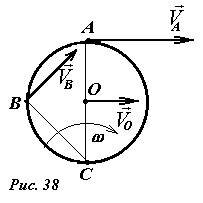
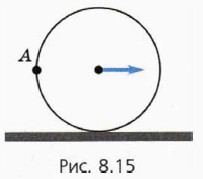
Рассмотренная задача об определении скоростей точек катящегося колеса может быть легко решена, если рассматривать его движение как поворот вокруг точки C (рис. 38): точка A находится на расстоянии 2R от мгновенной оси вращения, поэтому ее скорость равна V_A = 2Rω = 2V; точка B находится на расстоянии \(

R \sqrt<2>\) от оси, ее скорость \(

V \sqrt<2>\). Направления векторов скоростей также совпадают с полученными ранее.

Источник

Катящееся колесо

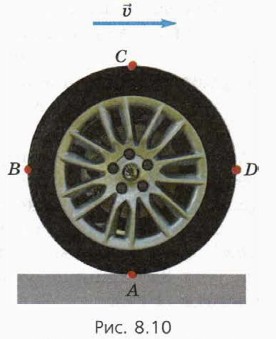
Рассмотрим движение различных точек колеса автомобиля.

Пусть автомобиль едет со скоростью (рис. 8.10), причём его колёса катятся без проскальзывания.

Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют чёткие следы). Этот факт — отправная точка для нахождения скорости всех других точек колеса — например, точек В, С, D на рисунке 8.10.

Чтобы найти скорость этих точек, удобно перейти в систему отсчёта, связанную с автомобилем, а потом вернуться в систему отсчёта, связанную с дорогой.

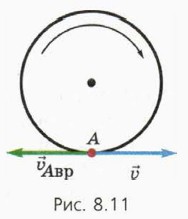
В системе отсчёта, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим υ_вр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля и и скорость вращения υ_вр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.

Заметим, что скорость _Авр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).

_А = _Авр + .

Итак, скорости _Авр и направлены противоположно, а их сумма _А = 0. Следовательно,

то есть скорость движения точек обода колеса в системе отсчёта, связанной с автомобилем, равна по модулю скорости автомобиля.

15. Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2υ.

16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.

17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью

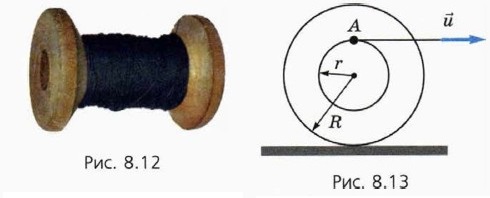
П о д с к а з к а. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.

18. С какой скоростью υ и в каком направлении будет двигаться катушка в случае, изображённом на рисунке 8.14?

Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.

19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.

П о д с к а з к а. Перейдите в систему отсчёта, связанную с велосипедистом.

Источник

Без проскальзывания что значит физика

Когда мы говорим «абсолютно гладкая поверхность» — это значит, что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.

Чаще при слове «трение» нам приходит в голову его «тёмная» сторона — из-за трения скрипят и прекращают качаться качели, изнашиваются детали машин. Но представьте, что вы стоите на идеально гладкой поверхности, и вам надо идти или бежать. Вот тут трение бы, несомненно, пригодилось. Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.

Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел.
Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.

Основная особенность: сила трения приложена к обоим телам, поверхности которых соприкасаются, и направлена в сторону, противоположную мгновенной скорости движения тел друг относительно друга. Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.

Откуда берётся трение

Трение возникает по двум причинам:

Виды силы трения

В зависимости от вида трущихся поверхностей, различают сухое и вязкое трение. В свою очередь, оба подразделяются на другие виды силы трения.

Сила трения покоя

Рассмотрим силу трения покоя подробнее.

Обычная ситуация: на кухне имеется холодильник, его нужно переставить на другое место.

Когда никто не пытается двигать холодильник, стоящий на горизонтальном полу, трения между ним и полом нет. Но как только его начинают толкать, коварная сила трения покоя тут же возникает и полностью компенсирует усилие. Причина её возникновения — те самые неровности соприкасающихся поверхностей, которые деформируясь, препятствуют движению холодильника. Поднатужились, увеличили силу, приложенную к холодильнику, но он не поддался и остался на месте. Это означает, что сила трения покоя возрастает вместе с увеличением внешнего воздействия, оставаясь равной по модулю приложенной силе, ведь увеличиваются деформации неровностей.

Пока силы равны, холодильник остаётся на месте:

Сила трения, которая действует между поверхностями покоящихся тел и препятствует возникновению движения, называется силой трения покоя

Сила трения скольжения

Что же делать с холодильником и можно ли победить силу трения покоя? Не будет же она расти до бесконечности?

Зовём на помощь друга, и вдвоём уже удаётся передвинуть холодильник. Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:

Теперь на движущийся холодильник действует сила трения скольжения. Она возникает при относительном движении контактирующих твёрдых тел.

Итак, сила трения покоя может меняться от нуля до некоторого максимального значения — Fтр. пок. макс И если приложенная сила больше, чем Fтр. пок. макс, то у холодильника появляется шанс сдвинуться с места.

Теперь, после начала движения, можно прекратить наращивать усилие и ещё одного друга можно не звать. Чтобы холодильник продолжал двигаться равномерно, достаточно прикладывать силу, равную силе трения скольжения:

Как рассчитать и измерить силу трения

Чтобы понять, как измеряется сила трения, нужно понять, какие факторы влияют на величину силы трения. Почему так трудно двигать холодильник?

Самое очевидное — его масса играет первостепенную роль. Можно вытащить из него все продукты и тем самым уменьшить его массу, и, следовательно, силу давления холодильника на опору (пол). Пустой холодильник сдвинуть с места гораздо легче!
Следовательно, чем меньше сила нормального давления тела на поверхность опоры, тем меньше и сила трения. Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.

Сила реакции опоры обозначается N. Можно сделать вывод

Второй фактор, влияющий на величину силы трения, — материал и степень обработки соприкасающихся поверхностей. Так, двигать холодильник по бетонному полу гораздо тяжелее, чем по ламинату. Зависимость силы трения от рода и качества обработки материала обеих соприкасающихся поверхностей выражают через коэффициент трения.

Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.

Он чаще всего попадает в интервал от нуля до единицы, не имеет размерности и определяется экспериментально.

Можно предположить, что сила трения зависит также от площади соприкасающихся поверхностей. Однако, положив холодильник набок, мы не облегчим себе задачу.

Ещё Леонардо да Винчи экспериментально доказал, что сила трения не зависит от площади соприкасающихся поверхностей при прочих равных условиях.

Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.

Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:

где μ — коэффициент трения, N — сила нормальной реакции опоры.

Для тела, движущегося по горизонтальной поверхности, сила реакции опоры по модулю равна весу тела:

Сила трения качения

Ещё древние строители заметили, что если тяжёлый предмет водрузить на колёсики, то сдвинуть с места и затем катить его будет гораздо легче, чем тянуть волоком. Вот бы пригодилась эта древняя мудрость, когда мы тянули холодильник! Однако всё равно нужно толкать или тянуть тело, чтобы оно не остановилось. Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.

Причина трения качения — деформация катка и опорной поверхности. Сила трения качения может быть в сотни раз меньше силы трения скольжения при той же силе давления на поверхность. Примерами уменьшения силы трения за счёт подмены трения скольжения на трение качения служат такие приспособления, как подшипники, колёсики у чемоданов и сумок, ролики на прокатных станах.

Направление силы трения

Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел. Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения.

Бывают ситуации, когда сила трения не препятствует движению, а совсем наоборот.

Представьте, что на ленте транспортёра лежит чемодан. Лента трогается с места, и чемодан движется вместе с ней. Сила трения между лентой и чемоданом оказалась достаточной, чтобы преодолеть инерцию чемодана, и эти тела движутся как одно целое. На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.

Если бы лента была абсолютно гладкой, то чемодан начал бы скользить по ней, стремясь сохранить своё состояние покоя. Напомним, что это явление называется инерцией.

Сила трения покоя, помогающая нам ходить и бегать, также направлена не против движения, а вперёд по ходу перемещения. При повороте же автомобиля сила трения покоя и вовсе направлена к центру окружности.

Для того чтобы понять, как направлена сила трения покоя, нужно предположить, в каком направлении стало бы двигаться тело, будь поверхность идеально гладкой. Сила трения покоя в этом случае будет направлена как раз в противоположную сторону. Пример, лестница у стены.