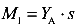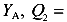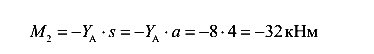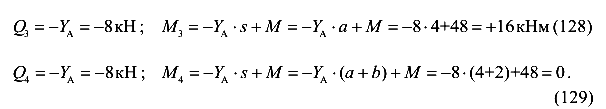в месте приложения сосредоточенной силы на эпюре моментов наблюдается

Десять правил анализа эпюр в балках

В о п р о с № 40. Построение эпюр внутренних сил в балках способом характерных сечений. Десять (золотых) правил анализа.

На балке выделяются особые сечения – точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки, места расположения опор, начало и конец балки. В этих сечениях вычисляются значения внутренних сил и наносятся на эпюры. Полученные точки соединяются с соблюдением следующих правил.

1. Анализ эпюр всегда выполнять слева направо. При анализе должны выйти из нуля и прийти в ноль.

2. В точке приложения сосредоточенного момента на эпюре изгибающих моментов M наблюдается разрыв (скачок) вниз, если момент направлен по ходу часовой стрелки, и вверх, если он направлен против хода часовой стрелки.

3. В точке приложения сосредоточенной силы на эпюре поперечных сил Q наблюдается разрыв (скачок) вниз, если сила направлена вниз, и разрыв (скачок) вверх, если сила направлена вверх.

4. В точке приложения сосредоточенной силы на эпюре изгибающих моментов M наблюдается излом с острием, направленным вниз, если сила направлена вниз, и вверх, если сила направлена вверх.

6. На участке балки, где приложена равномерно распределенная нагрузка q, эпюра поперечных сил Q имеет прямолинейный характер. Если нагрузка q направлена вниз, то поперечная сила Q уменьшается, а если вверх, то она увеличивается.

8. В поперечном сечении, где поперечная сила Q равна нулю на эпюре изгибающих моментов M наблюдается экстремум.

9. Площадь эпюры поперечных сил Q на участке балки равна изменению изгибающего момента M на этом участке при условии, что эпюра изгибающих моментов M не имеет разрыва.

10. Если на участке балки поперечная сила Q положительная, то изгибающий момент M увеличивается. И наоборот.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Теоретические предпосылки и указания к построению эпюр. Правила знаков для Q и M, проверки построения эпюр

Как построить эпюры Q и М. При прямом поперечном изгибе в поперечных сечениях балки возникает два внутренних силовых фактора – поперечная сила Q_y и изгибающий момент М_х. Для построения эпюр этих внутренних силовых факторов важно знать, чему они численно равны (определение) и правила знаков.

Поперечная сила, возникающая в сечении балки – это внутреннее усилие, равное алгебраической сумме проекций внешних сил, действующих по одну сторону от этого сечения на плоскость поперечного сечения.

Правило знаков. Положительная поперечная сила поворачивает рассматриваемую часть балки по часовой стрелке. (кратко – по часовой плюс, против – минус).

Изгибающий момент в сечении балки – это внутреннее усилие, равное алгебраической сумме моментов внешних сил, действующих по одну сторону от этого сечения, относительно центра тяжести сечения.

Правило знаков. Положительный изгибающий момент соответствует (т.е. вызывает) растяжению нижних волокон.

Для отыскания опасного сечения строят эпюры Q_y и М_х, используя метод сечения, либо метод характерных точек. Эпюра – это график, показывающий изменение того или иного фактора по оси балки. Сечения расставляются на характерных участках, характерный участок балки – это участок между какими-либо изменениями. Изменения – это сосредоточенные силы или моменты, начало и конец распределенной нагрузки. Характерные точки – это точки, сколь-либо заметные на балке, т.е. точки приложения сосредоточенных сил, моментов и т.д.

Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо мысленно рассечь плоскостью в этом месте балку и часть балки (любую), лежащую по одну сторону от рассматриваемого сечения, отбросить. Как правило, отбрасывают ту часть балки, которая представляется наиболее сложной. Затем по действующим на оставленную часть балки внешним силам надо найти искомые значения Q_y и М_х, причем знак их надо определить в соответствии с принятыми ранее правилами знаков.

При построении эпюры слева направо отбрасывается правая часть балки, а Q_y и М_х находятся по силам, действующим на левую часть. При построении эпюры справа налево, наоборот, отбрасывается левая часть, Q_y и М_х определяются по силам, действующим на правую часть балки.

Для построения эпюр проводят нулевые линии под изображением балки. Тогда каждому сечению балки соответствует определенная точка этой линии. Положительные значения поперечных сил откладывают в принятом масштабе перпендикулярно нулевой линии вверх от нее, отрицательные — вниз.

При построении эпюры М_х у строителей при­нято: ординаты, выражающие в определенном масштабе положительные значения изгибающих моментов, откладывать со стороны растянутых волокон, т.е. — вниз, а отрицательные — вверх от оси балки. У механиков положительные значения и поперечной силы и изгибающего момента откладываются вверх.

Найденные значения поперечной силы и изгибающего момента соединяют соответствующими линиями.

Построенные эпюры Q_уи М_xзаштриховывают прямыми линиями, перпендикулярными нулевой линии. Каждый штрих таким образом характеризует значение внутреннего силового фактора Q_у или М_x,действующих в дан­ном сечении балки. На эпюрах ставятся знаки.

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Задача 7

Построение эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры Q_у. Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Q_у ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Q_у в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно .

Строим эпюру Q_у методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также A и B – точки приложения опорных реакций, E– точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем:

Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Q_у. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Q_у (рис. б).

Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, рав­ный значению силы. Если наклонная линия под распределенной на­грузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Q_у и М_x, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов. В нашей задаче это точка К. Сосредоточенный момент на эпю­ре Q_у себя никак не проявляет, так как сумма проекций сил, образую­щих пару, равна нулю.

2. Построение эпюры моментов.Строим эпюру изгибающих моментов, как и поперечных сил, ме­тодом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значе­ния изгибающих моментов в начале участка, конце его и в одном проме­жуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в кото­ром эпюра Q_у пересекает нулевую линию, т.е. где Q_у= 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Q_у не пересекает нулевую линию, то для построения эпюры М следует на данном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если на­грузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпю­ры М. Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и бу­дет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.

Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточ­ных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствую­щих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соот­ветствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.

Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Q_у = 0.

Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,

Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):

Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Q_у (рис.б).

Определяем момент в точке К:

Пройдем оставшуюся часть балки ходом справа.

Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).

Источник

Построение эпюр внутренних сил в балках способом характерных сечений

Построение эпюр внутренних сил в балках способом характерных сечений. Десять (золотых) правил анализа

Отметим, что эти правила справедливы только в случае, если эпюра изгибающих моментов построена на растянутых волокнах балки

Пример:

Построения эпюр внутренних сил для элементарной балки методом характерных сечений (рис.49).

Рассмотрим пример, показанный на рисунке (рис.49, а). Вначале, используя уравнения статического равновесия, определим реакции на левой и правой опорах балки. Так как нам заранее неизвестны направления реакций, будем предполагать, что обе реакции направлены вверх. Составим уравнения равновесия.

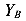
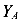
Реакция получилась отрицательной. Это опровергает наши предположения о направлении реакции на левой опоре. Исправим нашу ошибку и направим реакцию вниз (см. рис.49, а).

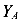
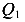
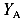
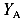
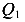
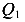
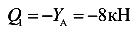
Рассмотрим часть балки, расположенной слева от сечения 1, к которой приложена единственная внешняя сила , направленная вниз и «пытающаяся» эту часть сдвинуть вниз. Материал сопротивляется такому сдвигу и в рассмотренном сечении появляется поперечная сила направленная вверх и равная реакции (рис.49, б). Обе силы и вызывают сдвиг, направленный против хода часовой стрелки. Согласно принятому правилу знаков для поперечных сил, поперечная сила принимается отрицательной и равной .

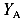
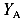
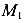
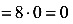
Плечо s реакции стремится к нулю, так как сечение 1 мы провели бесконечно близко к опоре А, располагая его справа (рис.49, б). Поэтому создать момент не может. Значит, материалу не чему сопротивляться, и изгибающий момент равен нулю .

Теперь проведем сечение 2 бесконечно близко к точке С слева и рассмотрим левую часть балки от этого сечения (рис.49, в). Повторяется ситуация, полученная для сечения 1. Поэтому и в сечении 2 появиться отрицательная сила равная реакции .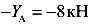

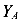
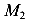
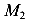
Реакция имеет плечо относительно сечения 2 и «пытается» повернуть левую часть балки против хода часовой стрелки. Материал сопротивляется и в сечении 2 появляется изгибающий момент , направленный по ходу часовой стрелки. Изображая изгибающий момент в виде пары сил, можно видеть, что верхняя стрелка вызывает растяжение верхних волокон, а нижняя — сжатие нижних волокон. Согласно правилу знаков для изгибающих моментов момент принимается отрицательным и равным

Аналогичными рассуждениями можно найти поперечные силы и изгибающие моменты в сечениях 3 и 4.

Проверим эпюры поперечных сил и изгибающих моментов, используя десять правил, приведенных выше.

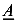
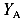
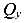
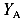
-в точке приложена сосредоточенная сила (реакция ) направленная вниз, поэтому на эпюре наблюдается скачок так же направленный вниз и равный значению ;

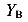
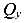
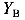
-в точке В приложена сосредоточенная сила (реакция ) направленная вверх, поэтому на эпюре наблюдается скачок так же направленный вверх и равный значению ;

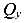
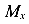
-на участке 1-2 нет распределенной нагрузки, поэтому эпюра постоянна, а эпюра имеет прямолинейный характер;

-на участке 1-2 поперечные силы отрицательные, поэтому изгибающие моменты при движении слева направо уменьшаются, при этом изменение изгибающих моментов равно площади эпюры ;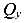

-в точке С к балке приложен сосредоточенный момент М, направленный против хода часовой стрелки, поэтому на эпюре изгибающих моментов наблюдается скачок, направленный вверх;

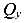
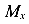
-на участке 2-3 нет распределенной нагрузки, поэтому эпюра постоянна, а эпюра имеет прямолинейный характер;

-на участке 2-3 поперечные силы отрицательные, поэтому изгибающие моменты при движении слева направо уменьшаются, при этом изменение изгибающих моментов равно площади эпюры .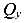

Таким образом, построенные эпюры поперечных и изгибающих моментов соответствуют выше перечисленным правилам. Следовательно, эпюры построены правильно. Построение эпюр методом сечений для балок с более сложной нагрузкой будут рассмотрены на практических занятиях.

Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:

Дополнительные страницы которые вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Построение эпюр изгибающих моментов и поперечных сил для балок

Автор: Константин Вавилов · Опубликовано 15.08.2015 · Обновлено 16.05.2018

Очень важно уметь строить эпюры для балок, работающих на изгиб! Так как построение эпюр, является неотъемлемой частью любого прочностного расчёта и большинство элементов, из которых состоят современные инженерные сооружения, работают на изгиб. Поэтому в сопромате, очень много внимания уделяется как раз данным эпюрам: поперечных сил и изгибающих моментов. Для краткости, их ещё называют эпюрой моментов и эпюрой сил. В этой статье, рассмотрим, как рассчитать эпюры традиционным методом, а также быстрым, с помощью которого эпюры рисуются за считаные минуты. В статье, построение показано на примере консольной и опирающейся на две опоры балки. Показано, как учитывать сосредоточенные силы и моменты, а также распределённые нагрузки.

Построение эпюр для консольной балки

Первым делом, вводим систему координат, ось x пускаем вдоль оси балки, ось y перпендикулярно ей, а ось z будет перпендикулярна плоскости, в которой размещены две первые оси и будет направлена «к нам».

В поперечных сечениях балки под действием приложенной нагрузки будут возникать два внутренних силовых фактора: поперечная сила и изгибающий момент. Наша задача выяснить, какой величины эти факторы во всех сечениях балки. Для наглядности, результат решения фиксируют в виде так называемых эпюр.

Эпюра строится по всей длине балки, ордината эпюры, под исследуемым сечением, показывает величину внутреннего усилия в этом сечении.

Эпюра поперечных сил

Начнём знакомство с поперечными силами с правила знаков для эпюр. После чего последовательно рассчитаем и построим эпюры для первого и второго участка балки.

Правило знаков для поперечной силы

При построении эпюр поперечных сил нужно придерживаться следующих правил знаков:

Возможно, сейчас будет немного непонятны данные правила, но прочитав следующие 2 блока статьи, вы поймёте, как применять эти правила в действии.

Поперечные силы на первом участке

Рассмотрим первым участок равный двум метрам. Сделаем мысленно сечение на расстоянии x₁ от свободного торца и запишем законы изменения эпюр на этом участке. Законы эти выражаются из уравнений равновесия статики. Статика говорит нам, что тело находится в равновесии, если выполняются следующие условия:

Если суммы проекций всех сил на обе оси равны нулю и сумма моментов относительно точки равна нулю.

Для поперечной силы возьмём сумму проекций на ось y:

Поперечные силы на втором участке

На втором участке, поперечная сила будет равна: Q_{y 2} = Q_{y 1} ;

Так как на этом участке, действует все та же сила F. Момент в уравнениях поперечных сил не учитывается, что является следствием уравнений статики.

Эпюра изгибающих моментов

Правила знаков для изгибающих моментов

То есть, обычно, при построении эпюр изгибающий моментов знаки не указываются. Эти эпюры откладываются со стороны «растянутых волокон». Так, и удобнее читать эпюры и откладывать их.

Не всегда их откладывают так! Студентов некоторых специальностей, чаще всего машиностроительных, учат откладывать эпюры со стороны «сжатых волокон». Строители откладывают со стороны «растянутых волокон», в своих статьях я буду придерживаться этого правила, так как привык к нему.

Изгибающий момент на первом участке

Это закон изменения изгибающих моментов по длине участка. В отличие от поперечных сил, изгибающие моменты будут меняться в пределах этого участка.

Источник