точка приложения движущей силы
Что такое точка приложения силы?
Точки приложения силы
Первым научным сочинением Карно был трактат «Опыт о машинах вообще», изданный анонимно в 1783 г. В третьем издании (1803) трактат был расширен и переименован: он стал называться «Основные принципы равновесия и движения».
Одна из главных проблем этого сочинения – вывод условия равновесия машины при помощи расчета приращения работы силы на виртуальных перемещениях точек приложения сил (термин «работа» был введен в XIX в.).
Для вывода этого условия Карно ввел заменяющую схему грузов, производящих в точках системы те же действия, что и произвольная система сил. Идея вводить заменяющую схему грузов вместо сил оказалась в XVIII в. чрезвычайно плодотворной, она использовалась в аналитической статике многими современниками Карно – Лагранжем, Фурье, Ампером и др. Заменяющие схемы (блоков, рычагов, полиспастов и т. д.) при выводе начала возможных перемещений свидетельствуют о тесной связи этого начала с техникой машин и механизмов. Само начало возможных перемещений выросло на почве изучения машин, и в обоснованиях его с помощью заменяющих схем видны следы технического происхождения этой теории.
Карно ввел понятие геометрического движения, т. е. такого, которое допускается связями (в современной терминологии следовало бы уточнить: идеальными, удерживающими). В современной механике «геометрическим движениям» соответствуют виртуальные перемещения точек системы.
Карно рассматривает некоторую механическую систему (машину), в произвольных точках которой приложены силы. Скорости, которые могут иметь точки приложения сил в первое мгновение геометрического движения, угол между направлением силы и скорости. Карно выводит условие равновесия «машин» под действием заданных сил. Он рассуждает следующим образом.
Действие сил в точках их приложения можно заменить действием грузов. Для этого в каждой точке приложения силы нужно прикрепить нить (невесомую, нерастяжимую), идущую вдоль направления приложенной силы и переброшенную через неподвижный блок. К свободно свисающему отвесному концу нити ниже блока нужно привязать гирю весом, равным по величине интенсивности силы. В результате Карно приходит к системе грузов или гирь; равновесие полученной системы трактуется с помощью принципа Торричелли о наинизшем положении ее центра тяжести. Как и Торричелли, Карно вместо условия минимальности высоты центра тяжести системы грузов записывает условие экстремальности вертикальной координаты центра тяжести.
Равенство представляет собой едва ли не самую первую аналитическую запись принципа виртуальных скоростей.
Выражение, стоящее под знаком суммы, Карно называл «моментом активности». Он придавал этой количественной характеристике исключительно большое значение в теории машин. Карно считал, что именно это количество нужно по возможности экономить, чтобы извлечь из двигателя весь тот эффект, который он способен дать. Пользуясь современным языком, это выражение под знаком суммы можно назвать виртуальной мощностью машины (т. е. работой всех приложенных сил на виртуальных перемещениях точек приложения в единицу времени). Карно приближается к введению понятия полезной мощности или полезного действия машины.
I. Механика
Тестирование онлайн
Что надо знать о силе
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
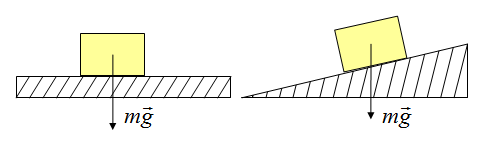
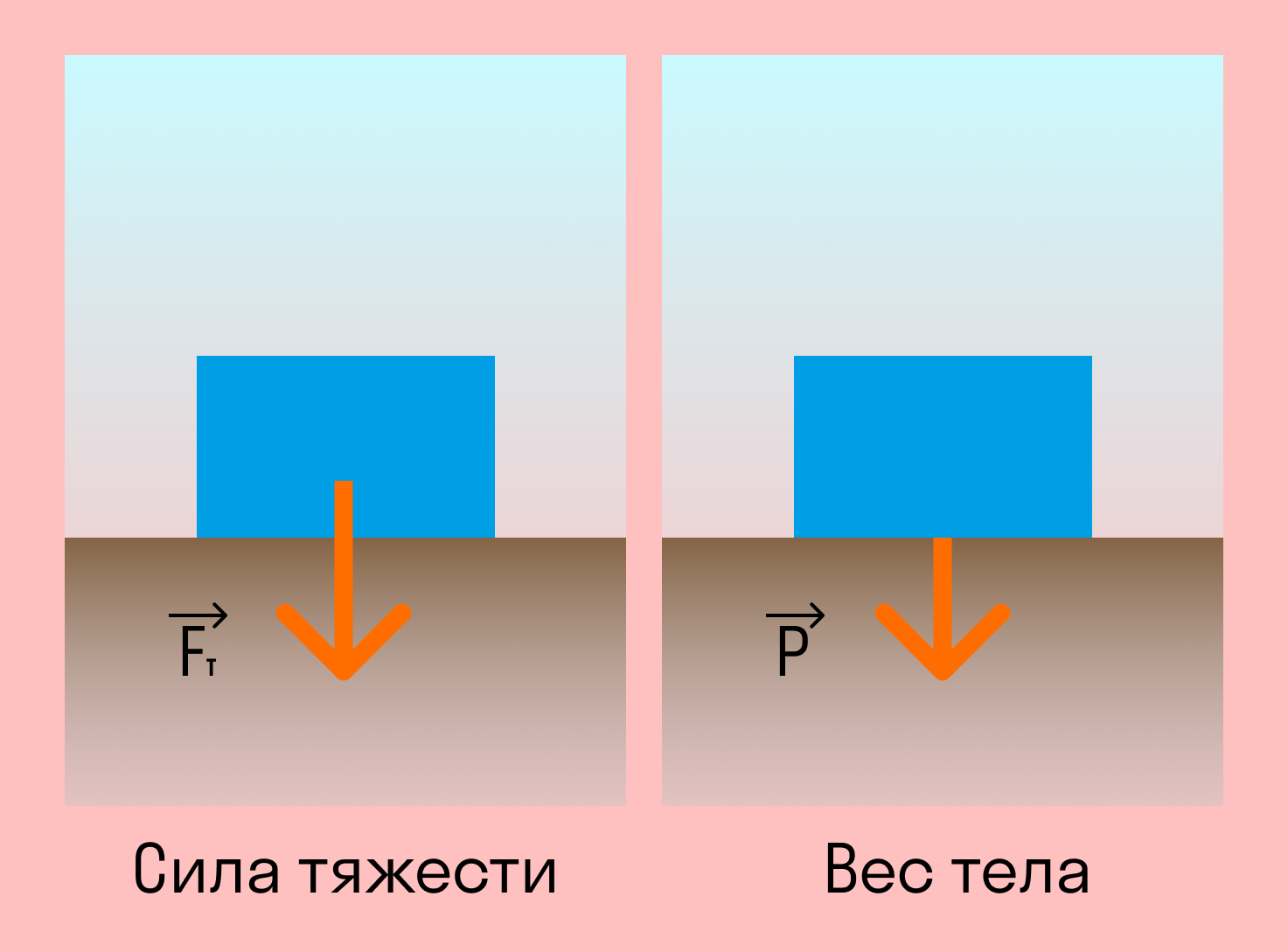
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
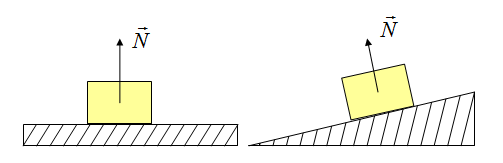
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой 
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости

Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
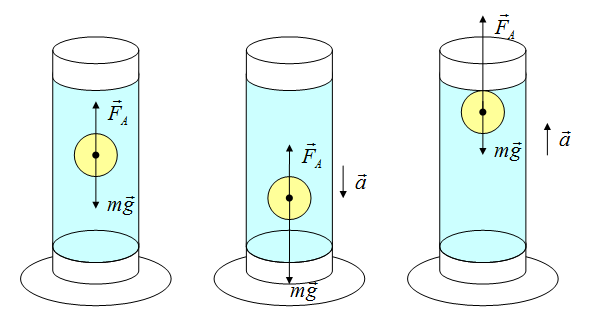
Вес тела
Формулы определения веса нет. Обозначается эта силы буквой 
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
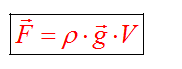
В воздухе силой Архимеда пренебрегаем.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Силы трения*
Трение качения определяется по формуле

Сила сопротивления возникает при движении тела в жидкости или в газе. Величина силы сопротивления зависит от размеров и формы тела, скорости его движения и свойств жидкости или газа. При небольших скоростях движения сила сопротивления пропорциональна скорости тела
При больших скоростях пропорциональна квадрату скорости
Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения*
Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила 
А сейчас сравним закон гравитации и силу тяжести
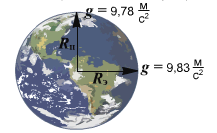
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
Презентация была опубликована 6 лет назад пользователемАнжела Демидова
Похожие презентации
Презентация на тему: » Сила Лоренца Сила Лоренца – сила, с которой магнитное поле действует на движущуюся электрически заряженную частицу. 1) Точка приложения – движущаяся заряженная.» — Транскрипт:
1 Сила Лоренца Сила Лоренца – сила, с которой магнитное поле действует на движущуюся электрически заряженную частицу. 1) Точка приложения – движущаяся заряженная частица (заряд). 2) Направление силы Лоренца определяется правилом левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали с направлением движения положительного заряда (против движения отрицательного), то отогнутый под прямым углом в плоскости ладони большой палец покажет направление действия силы Лоренца.
2 Сила Лоренца всегда перпендикулярна вектору скорости движения заряда. Такая сила не совершает работы, т. е. сила Лоренца не может изменить модуля скорости заряда. Она лишь сообщает заряду нормальное (центростремительное) ускорение и меняет направление его движения. Если заряд движется перпендикулярно линиям однородного магнитного поля, то его траектория – окружность.
3 Модуль силы Лоренца может быть выражен из модуля силы Ампера: Где В – модуль вектора магнитной индукции, q – величина заряда, υ – модуль скорости заряда, α – угол между направлением вектора магнитной индукции и вектора скорости заряда.
5 Применение силы Лоренца Циклотрон – ускоритель тяжелых частиц (протонов, ионов). Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна частоте обращения заряда. Заряженные частицы испускаются в центре камеры. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем.
6 Если скорость частицы не перпендикулярна вектору магнитной индукции, то такая частица будет двигаться в однородном магнитном поле по спирали. Радиус спирали R будет зависеть от модуля составляющей скорости, перпендикулярной магнитному полю, а шаг спирали h – от модуля составляющей скорости, параллельной полю.
Вес тела
Невесомость: что это такое
Невесомость — это состояние, при котором тело не давит на опору или подвес.
Само слово «невесомость» как бы подсказывает нам, что веса здесь быть не должно. При этом непонятно, что с ним тогда происходит. Давайте разбираться.
Вес тела
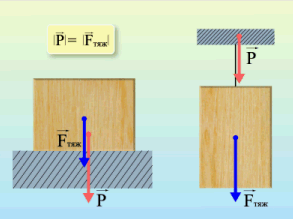
Вес — это сила, с которой тело действует на опору или подвес. Измеряется вес, как и любая другая сила, в Ньютонах.
«Но погодите! Вес же измеряют в килограммах — я вот вешу 50»
Это не совсем верно. В быту мы часто подменяем понятие «масса» понятием «вес» и говорим: вес чемодана — десять килограммам. В физике это два совершенно разных понятия, которые при этом взаимосвязаны.
Если у вас неподалеку есть весы — приглашаем в эксперимент! Один нюанс: наша затея сработает именно с механическими весами, но не с электронными. Поехали!
Шаг 1. Если встать на весы ровно и не двигаться — ваш вес будет высчитываться по формуле:
P = mg
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с2
Здесь может возникнуть два возражения:
Точка приложения силы. Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Весы измеряют силу. Весы работают таким образом, что измеряют вес тела — силу, с которой мы на них действуем, а показывают — массу. Можно сделать вывод, что весы — это динамометр (прибор, измеряющий силу).
Шаг 2. Теперь пошалим и резко встанем на носочки! Стрелка резко отклонилась влево, а потом вернулась на место. Вы придали себе ускорение, направленное вверх — в то время, как ускорение свободного падения всегда направлено к центру Земли (вниз).
Теперь вес тела вычисляем по формуле:
P = m (g-a)
g — ускорение свободного падения [м/с2]
a — ваше ускорение [м/с2]
На планете Земля g = 9,8 м/с2
Шаг 3. Последняя часть эксперимента — резко опуститься на пятки. Теперь вы сильнее давите на весы, потому что придали ускорение, направленное вниз. Стрелка весов отклонится вправо и вернется на место, когда вы придете в состояние покоя.
Формула веса примет вид:
P = m (g+a)
g — ускорение свободного падения [м/с2]
a — ваше ускорение [м/с2]
На планете Земля g = 9,8 м/с2
Кстати, если ровно стоять на весах, но взвешиваться в лифте — все будет работать наоборот. Если лифт едет вверх, то он как будто давит весами на человека, стоящего на них, а это как раз ситуация с увеличением веса. А если вниз — весы как будто бы от вас «убегают», чтобы показать меньшее значение.
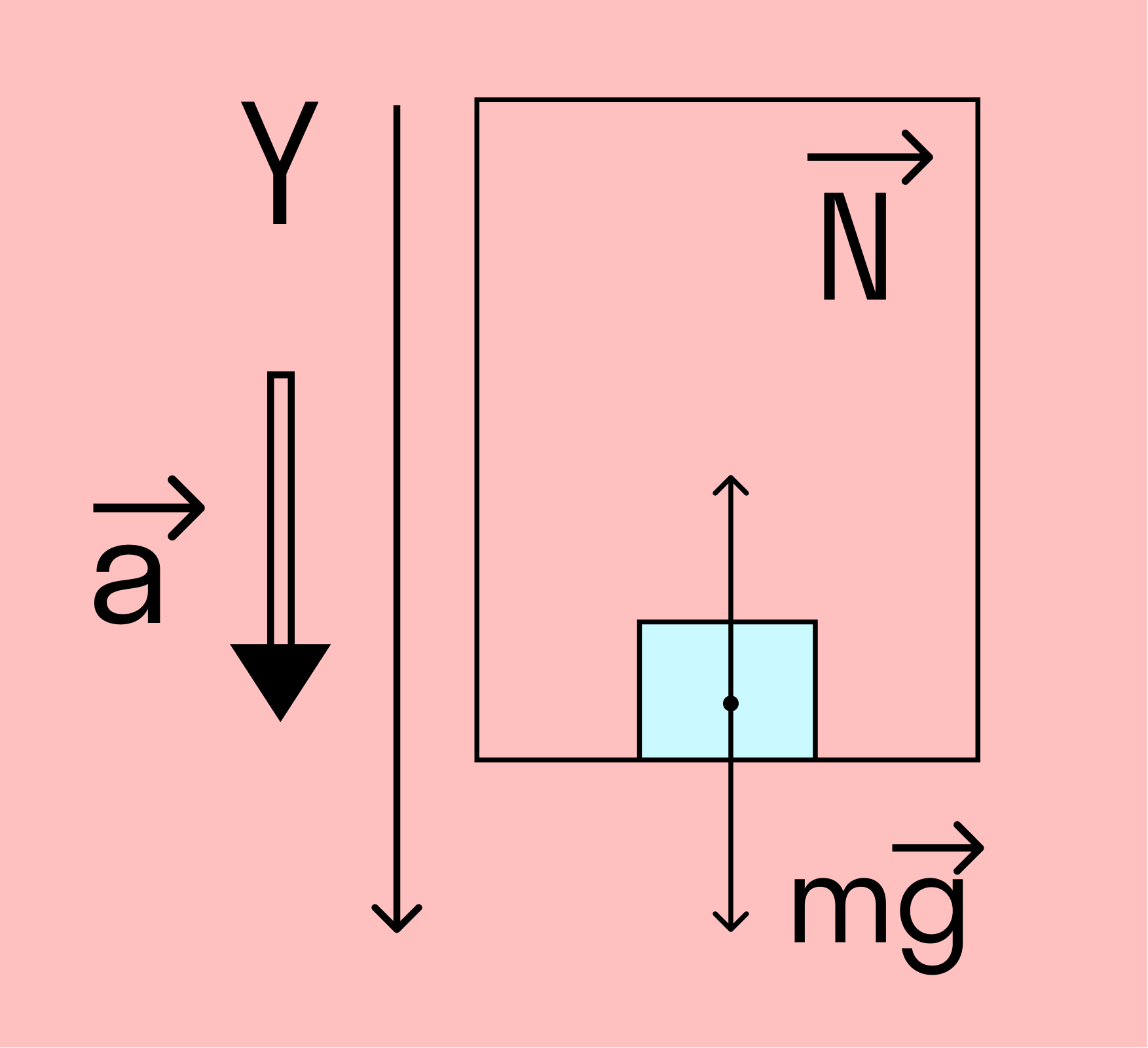
Этот случай мы можем описать через 2 закон Ньютона. Возьмем лифт, который едет вниз. Обозначим силы на рисунке.
N – сила реакции опоры [Н];
mg – сила тяжести [Н];
a – ускорение, с которым движется лифт [м/с2].
При проецировании на ось y, направленную вниз, мы получаем:
А теперь нам понадобится третий закон Ньютона — по нему сила реакции опоры равна весу тела:
Снова невесомость
Ну что, с весом разобрались. А теперь давайте сделаем так, чтобы его не стало и получилась та самая невесомость.
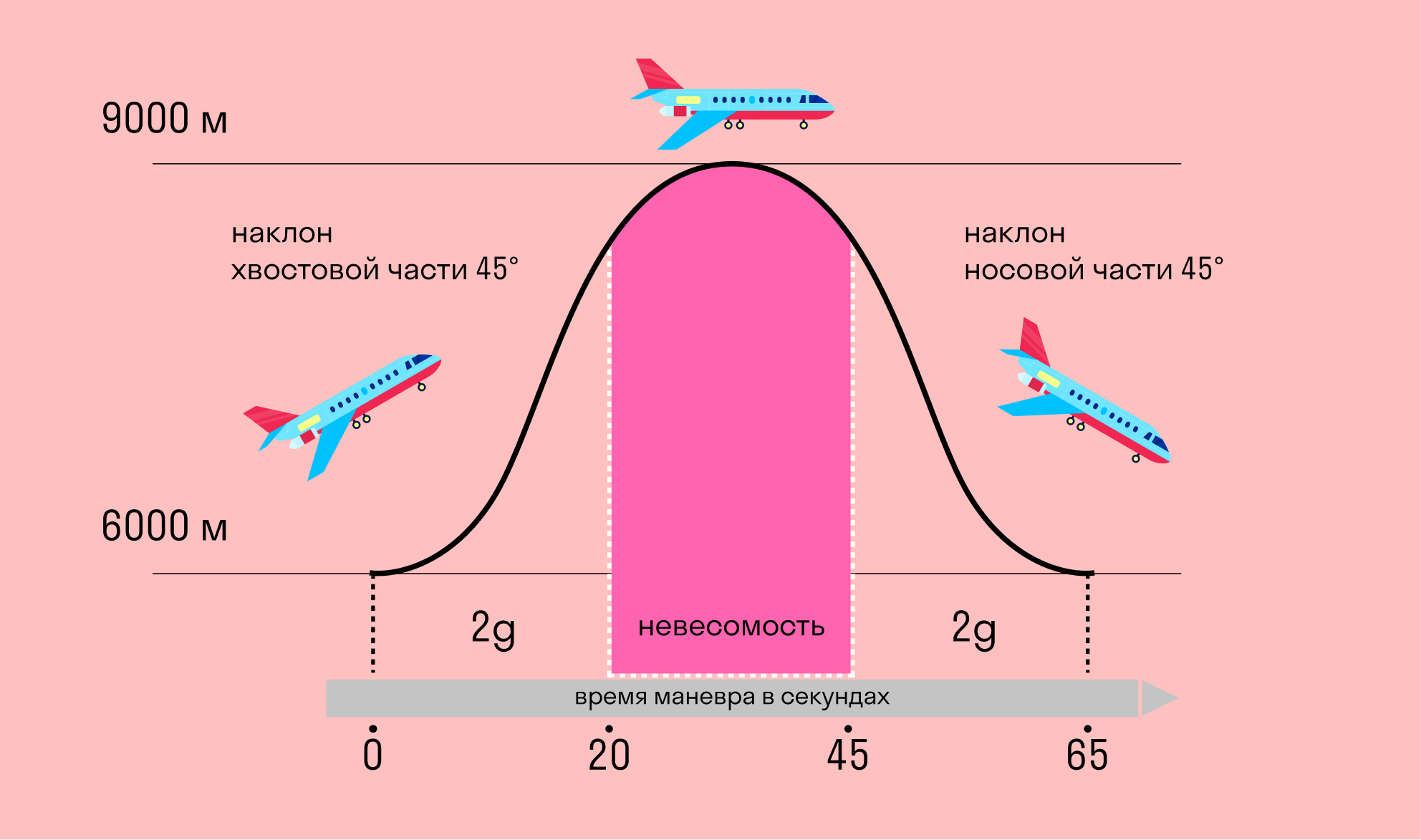
Чтобы привыкнуть к ощущению невесомости в космосе, космонавты тренируется в специальных самолетах-лабораториях:
Он взлетает и начинает просто падать, чтобы ускорение самолета было равно ускорению свободного падения. В этот момент, в формуле веса из g вычитается равное ему значение и получается 0:
Вот мы и в невесомости!
Если они летят вокруг Земли, то да. Как писал Дуглас Адамс в книге «Автоспом по галактике»: «Летать просто. Нужно просто промахнуться мимо Земли».
Когда космический корабль обращается вокруг Земли, он просто пытается на нее упасть, но промахивается. Такой процесс происходит, когда корабль движется с первой космической скоростью, равной 7.9 км/с. Это та скорость, с которой корабль становится искусственным спутником Земли.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы. Такие дела 🙂
Учебники
Журнал «Квант»
Общие
Зильберман А. Р. Равнодействующая — как ее найти? //Квант. — 1988. — № 11. — С. 50-52.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Мы часто решаем задачи «с практическим содержанием», вовсе не отдавая себе отчета, насколько они сложны. Даже простой автомобиль содержит тысячи деталей, на каждую из которых действует множество сил. Просто перечислить их — и то трудно, а написать и решить столько уравнений. Однако мы умудряемся обойти это затруднение, вводя понятие равнодействующей силы. Поговорим об этом подробнее.
Для определения равнодействующей нужно все силы, действующие на тело, векторно сложить (не всегда это просто, но об этом чуть позже). Полученный суммарный вектор будет эквивалентен исходной системе сил.
Так уж и эквивалентен? Представьте, что лично вас тянут с силой 500 Н влево за левую руку и с такой же силой — вправо за правую руку. Сумма этих сил равна нулю, т. е. их как бы нет вовсе. Вам от этого легче?
На самом деле эквивалентность тут понимается в довольно узком смысле — при замене всех сил их равнодействующей не должно измениться движение тела, а вот о деформациях, разрывах и т. п. речи нет.
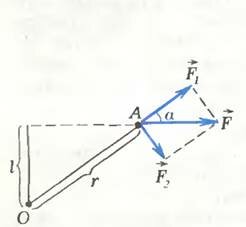
Какие же трудности могут возникнуть при сложении сил? Бели все они приложены в одной точке — то никаких. И складывать легко, и ясно, куда приложить суммарный вектор — равнодействующую. А если силы приложены в разных точках (чаще всего так и бывает)? Тогда придется силы переносить. Как это можно сделать? Тут нам понадобится специальная физическая величина — момент силы.
\vec F\) относительно точки О (рис. 1) равен
где r — расстояние от точки О до точки приложения силы А. Можно сделать иначе — разложить силу \(
\vec F\) на две составляющие — вдоль r и перпендикулярно r. Вращающий момент создает только перпендикулярная составляющая \(
Конечно, это просто предыдущая формула, переписанная немного иначе, но во многих задачах удобнее пользоваться именно ею.
Легко видеть, что при переносе силы \(
\vec F\) вдоль линии ее действия момент силы не изменяется, поэтому такой перенос допустим. (Заметим, что деформации тела при переносе точки приложения силы изменяются. Это легко понять на простом примере. Потянем привязанную одним концом к стене резиновую ленту вначале за середину, а потом за второй конец — она растянется неодинаково.)
Теперь вернемся к равнодействующей. Если силы приложены в разных точках, но линии их действия пересекаются в одной,— опять все просто. Перенесем силы вдоль линий их действия в эту точку и сложим — все, как в первом случае. Бели же линии действия сил не пересекаются в одной точке, задача нахождения равнодействующей усложняется.
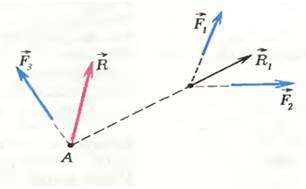
Разберем для простоты частный случай, когда все векторы сил лежат в одной плоскости (плоская система сил). Можно попробовать решить задачу за несколько шагов — складывая силы попарно, как показано на рисунке 2. Вначале сложим силы \(
\vec F_2\) — получим вектор \(
\vec R_1\), а потом сложим его с вектором \(
\vec F_3\). Равнодействующая \(
\vec R\) приложена в точке А.
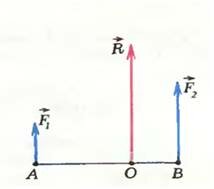
Так можно получить ответ не во всех случаях. Проблемы возникают, если векторы сил параллельны. Рассмотрим пример: нужно найти равнодействующую параллельных сил \(
\vec F_2\) (рис. 3). Ясно, что модуль равнодействующей равен сумме F1 и F2, а вот в какой точке должна быть приложена равнодействующая? Тут поможет простое рассуждение: какую бы точку приложения мы ни взяли, все равно момент равнодействующей относительно оси, проходящей через эту точку, равен нулю. Но при замене сил их равнодействующей моменты меняться не должны — значит, нужно взять такую точку, относительно которой суммарный момент исходной системы сил равен нулю. В нашем примере эту точку О можно найти из условия
\vec F_2\) направлены в разные стороны, то точка О окажется за пределами отрезка АВ, ближе к той из сил, которая по величине больше. (Убедитесь в этом самостоятельно.)
Задачи, где нужно находить равнодействующую параллельных сил, вы наверняка решали. Так, обычно силы тяжести, приложенные к разным частям тела, считают параллельными. Центр тяжести тела — это как раз и есть точка приложения равнодействующей этих сил. Вот почему, например, тело, закрепленное на оси, которая проходит через центр тяжести тела, находится в равновесии.
Есть один важный частный случай параллельной системы сил, когда равнодействующую найти нельзя. Так будет для двух параллельных сил, которые равны по величине и противоположны по направлению. Эту систему называют парой сил. Попытка найти точку приложения пары сил приводит к делению на нуль — найти эту точку не удается. У пары сил есть одно интересное свойство: ее момент одинаков относительно любой оси вращения (проверьте это). Оказывается, таким свойством обладает любая система сил, сумма которых равна нулю (пара сил — частный случай такой системы).
Но именно такими системами сил мы и интересуемся, когда говорим об условиях равновесия тел (статика). Одно из условий — сумма сил равна нулю. Отсюда вытекает важное следствие: уравнение моментов, т. е. второе условие равновесия — сумма моментов равна нулю, можно записывать в этом случае относительно любой точки, в том числе и не лежащей внутри тела. Эту точку следует выбирать из соображений простоты получающегося уравнения (удобно ее взять, например, на пересечении линий действия нескольких сил, особенно тех, которые мы не хотим находить).