по способу приложения поверхностные силы могут быть

Внешние и внутренние силы. Метод сечений

Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые на­зываются внешними. Внешние силы, действующие на тело, мож­но разделить на активные (независимые) и реактивные. Реак­тивные усилия возникают в связях, наложенных на тело, и опреде­ляются действующими на тело активными усилиями.

По способу приложения внешние силы делятся на объемные и поверхностные.

Скорость роста усилий при динамическом нагружении не обеспечивает равновесности процессов, протекающих в материале, в результате чего возникают многочисленные нарушения внутренней структуры материала. При систематическом чередовании нагружения и разгрузки накопление дефектов структуры ведет к возникновению микроскопических трещин, слияние которых приводит к усталостному разрушению.

Взаимодействие между частями рассматриваемого тела характе­ризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмоле­кулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой.

В брусе сечение проводят перпендикулярно его оси. Такое сечение называют поперечным.

Величины внутренних усилий определяются с применением метода сечений, суть которого заключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.

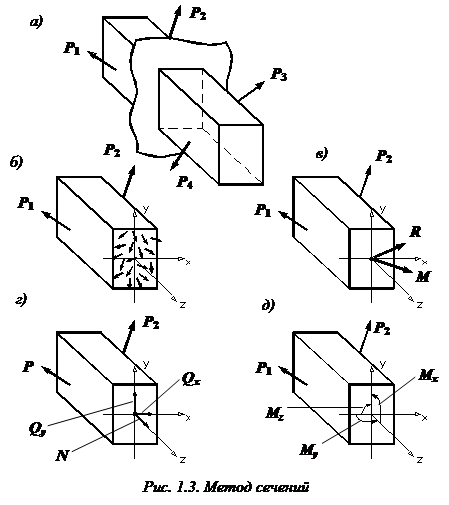
Рассмотрим тело, имеющее форму бруса (рис. 1.4, а).

Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (P_А ), действующей в сечении А (рис. 1.4, б).

Рис. 1.4

Обозначая через и суммы внешних сил, приложен­ных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что

(1.1)

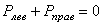
для отсеченных частей бруса получим следующие очевидные соот­ношения:

; . (1.2)

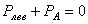
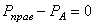
Последние соотношения показывают, что равнодействующая внутренних сил Р_А в сечении А может определяться с равным успе­хом из условий равновесия либо левой, либо правой частей рассе­ченного тела. В этом сутьметода сечений.

Внутренние усилия должны быть так распределены по сече­нию, чтобы деформированные поверхности сечения А при совме­щении правой и левой частей тела в точности совпадали. Это тре­бование в механике твердого деформируемого тела носит название условия неразрывности деформаций.

При известных внешних силах все шесть внутренних силовых факторов в сечении определяются из шести уравнений равновесия, которые могут быть составлены для отсеченной части.

(1.3)

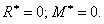
Последние два векторные уравнения равновесия дают шесть скалярных уравнений в проекциях на декартовых осях координат:

(1.4)

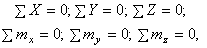
которые, в общем случае составляют замкнутую систему алгебраических уравнений относительно шести неизвестных внутренних усилий: , , , , , .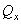

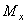
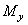
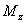
Рис. 1.5

Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.

Таблица 1.1. Простейшие случаи сопротивления

Сопротивления, при которых в поперечном сечении бруса дей­ствует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий (например, изгиб с кручением) сопротивление бруса называется сложным.

В заключение заметим, что при выполнении практических рас­четов, для наглядности, как правило, определяются графики функ­ций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изме­нения внутренних усилий вдоль продольной оси стержня называ­ются эпюрами.

Источник

iSopromat.ru

Все внешние силы (нагрузки), действующие на изучаемое тело, следует рассматривать как проявление взаимодействия его с окружающими телами, которое представляется в виде сил или пар сил (моментов).

Все внешние силы (нагрузки) могут рассматриваться как сосредоточенные или распределённые.

В природе сосредоточенных сил не бывает. Все реальные тела практически контактируют через небольшие площадки. Однако принцип Сен-Венана позволяет распределенную нагрузку заменить равнодействующей силой, что упрощает расчёт.

Сосредоточенные нагрузки выражаются в ньютонах [H] и обозначается буквой F.

Распределённые нагрузки обозначаются буквой q и они бывают:

Сосредоточенные и распределённые нагрузки могут быть как статическими, так и динамическими.

Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.

Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут многократно превосходить те же нагрузки, приложенные статически.

Законы изменения нагрузок во времени могут иметь весьма сложный характер.

В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.

Классификация внешних нагрузок

Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками.

По способу приложения нагрузки бывают объемные и поверхностные, распределенные и сосредоточенные, по характеру изменения в процессе приложения – статические, динамические и повторно-переменные, по продолжительности действия – постоянные и временные.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

НАГРУЗКИ ПО СПОСОБУ ПРИЛОЖЕНИЯ

По способу приложения нагрузки бывают объемными (собственный вес, силы инерции), действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные нагрузки и распределенные нагрузки.

В сопромате часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно q и выражаемой в ньютонах на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м, кгс/см) и т.д.

НАГРУЗКИ ПО ХАРАКТЕРУ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ

Вопрос

1. Брус — любое тело, у которого длина значительно больше других размеров.

В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев:

— прямой брус постоянного поперечного сечения (рис. 4.4, а);

— прямой ступенчатый брус (рис. 4.4, 6);

— криволинейный брус (рис. 4.4, в).

2. Пластина — любое тело, у которого толщина значительноменьше других размеров (рис.4.5).

3. Массив — тело, у которого три размера одного порядка.

Вопрос

Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

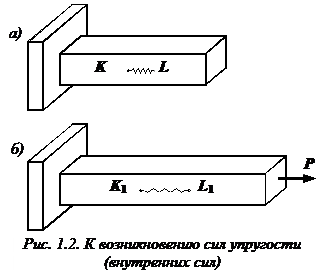
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).

Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.

Приложим теперь к стержню растягивающую силу (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение , а частица L – в положение . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и Lблагодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.

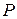
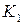
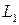
ВНУТРЕННИЕ СИЛЫ В МЕТОДЕ СЕЧЕНИЙ

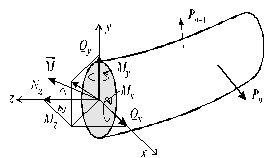
Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).

Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.

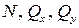
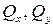
Получим 6 внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы (рис. 1.3, г) и три момента (рис. 1.3, д).

– поперечные силамы,

момент относительно оси z ( 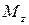) – крутящий момент

моменты относительно осей x, y ( 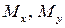) – изгибающие моменты.

Запишем для оставленной части тела уравнения равновесия (уравновесим):

.

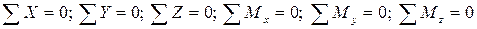
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.

Вопрос

Переменное напряжение

Напряжения, переменные во времени, возникающие в элементах конструкции под действием нагрузок, переменных по величине или направлению, а также нагрузок, перемещающихся относительно рассматриваемого элемента.

Допускаемое напряжение

Экспериментально установленное для рассматриваемого материала предельное значение напряжения, деленное на коэффициент запаса прочности.

Главное напряжение

Среди множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки и возникающие на них нормальные напряжения называются главными.

Источник

Как классифицируются внешние силы?

Внешние силы, действующие на конструкцию, делятся на активные, которые принято называть нагрузками, и реактивные – реакции связей.

По способу приложения нагрузки могут быть объемными (собственный вес, силы инерции), то есть действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные и распределенные.

В сопротивлении материалов часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно буквой q и выражаемой в ньютонах (килоньютонах) на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м)и т. д.

Реальные нагрузки, действующие на конструкцию, не всегда могут быть сведены лишь к сосредоточенным и распределенным нагрузкам. Возможны и моментные воздействия, например, в виде сосредоточенных моментов. Последние выражаются в единицах силы, умноженных на единицу длины (кН·м, кгс·м и т. д.). Напомним, что термины «сосредоточенный момент», «пара», «плечо» были введены в 1804 г. французским ученым Луи Пуансо (Poinsot,1777–1859 гг.).

По характеру изменения во времени нагрузки бывают статические (нарастающие медленно от нуля до своего конечного значения и в дальнейшем не изменяющиеся) и динамические (изменяющиеся с течением времени свою величину и (или) точку приложения и при этом изменяющие их достаточно быстро).

1.9. Какие основные допущения принимаются в сопротивлении материалов?

Структура реальных твердых тел настолько сложна, что они в своем естественном виде не могут стать предметом изучения в сопротивлении материалов. Твердые тела приходится идеализировать, то есть наделять их такими свойствами, которые, с одной стороны, достаточно точно передают основные характеристики реальных твердых тел, а с другой стороны, являются достаточно простыми для их представления в виде математических соотношений. Целью такой идеализации является получение определенных законов в виде уравнений, правильно описывающих основные свойства твердого тела.

При построении теории расчета на прочность, жесткость и устойчивость принимаются допущения, относящиеся как к свойствам материалов, так и допущения, связанные с деформацией твердого тела.

К первой группе допущений относятся следующие:

1) Считается, что материал твердого тела представляет собой сплошную среду, то есть полагают, что материал полностью заполняет весь объем тела, без каких-либо пустот. Это представление о твердом теле, как о сплошной среде, дает возможность применять при исследовании его напряженно-деформированного состояния методы дифференциального и интегрального исчислений, которые требуют непрерывности функции в каждой точке объема тела.

2) Материал считается однородным, то есть его физико-механические свойства являются одинаковыми во всех точках тела.

3) Материал считается изотропным, то есть его физико-механические свойства в каждой точке тела одинаковы во всех направлениях. Материал, не обладающий этим свойством, называется анизотропным. К анизотропным материалам, например, относится дерево.

4) Полагают, что материал является идеально упругим, то есть после снятия внешней нагрузки его деформация полностью исчезает.

Вторая группа допущений связана с деформацией твердого тела:

1) Деформации считаются малыми. Отсюда следует, что при составлении уравнений равновесия, а также при определении внутренних сил можно не учитывать деформацию тела. Это допущение иногда называют принципом начальных размеров.

Рассмотрим, например, стержень, заделанный одними концом в стену и нагруженный на свободном конце сосредоточенной силой P (рис. 1.1).

Определим значение реактивного момента , возникающего в
жесткой заделке. Для этого воспользуемся соответствующим уравнением равновесия, известного уважаемому Читателю, из теоретической механики:

.

Отсюда легко можно найти, что .

Но все ли здесь нами выполнено правильно? К сожалению, нет. Ведь прямолинейное положение стержня вовсе не является его положением равновесия. Под действием силы P стержень неизбежно изогнется. При этом точка приложения нагрузки сместится как по вертикали, так и по горизонтали.

Если записать уравнение равновесия стержня для деформированного (изогнутого) состояния, то реактивный момент, возникающий в заделке, окажется равным:

.

Принимая в сопротивлении материалов упомянутое выше допущение о малости деформаций, мы полагаем, что перемещением w можно пренебречь по сравнению с длиной стержня l, то есть . Тогда, действительно, мы получим, что .

Однако необходимо помнить, что допущение о малости деформаций не всегда является справедливым.

Заметим, что иногда принцип начальных размеров называют принципом отвердения, что не совсем верно. Принцип отвердения используется, например, при изучении поведения жидких тел. Если такая система находится в равновесии, то можно предположить, что она отвердела и сделалась неизменяемой. И тогда к ней можно будет применить уравнения равновесия твердого тела.

2) Полагают, что перемещения точек твердого тела пропорциональны внешним нагрузкам, вызывающим эти перемещения, то есть считается, что тело является линейно деформируемым.

Необходимо отметить, что допущение о линейной деформируемости конструкции нельзя отождествлять с законом Гука, как это делается, к сожалению, в некоторых учебниках по сопротивлению материалов.

Дело в том, что закон Гука, о котором мы будем говорить подробнее в следующей беседе, устанавливает линейную зависимость между
внутренними силами и деформациями, а не внешними силами и перемещениями.

3) Для линейно деформируемых конструкций справедлив принцип независимости действия сил (принцип суперпозиции). Этот принцип формулируется следующим образом.

Результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности.

В основе этого принципа лежит допущение о малости деформаций, а также предположение об обратимости процессов нагрузки и разгрузки конструкции.

1.10. В чем заключается суть метода сечений и для чего он применяется?

Метод сечений позволяет определить внутренние силы (точнее говоря, внутренние силовые факторы), которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

Рассмотрим, например, идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).

Мысленно выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.

Приложим теперь к стержню растягивающую силу (рис. 1.2, б). Пусть в результате деформации стержня частица K перейдет в положение , а частица L – в положение . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называется силой упругости или внутренней силой. Она, как уже отмечалось, может быть найдена методом сечений.

Метод сечений подразделяется на четыре этапа. Для лучшего запоминания формулировки методаи его четырех этапов иногда вводится аббревиатура РОЗУ, представляющая начальные буквы наименований соответствующих этапов: разрежем, отбросим, заменим, уравновесим.

Мысленноразрежем стержень, находящийся в равновесии под действием некоторой системы (рис. 1.3, а), на две части плоскостью, перпендикулярной к его оси z.

Напомним, что реакции связей также относятся к внешним силам, поэтому среди сил, показанных на рис. 1.3, могут быть как активные, так и реактивные силы.

Отбросим одну из частей стержня, например, переднюю и рассмотрим оставленную нами часть.

Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые возникли между этими частицами вследствие деформации тела.

Иными словами, действие отброшенной передней части стержня вместе с приложенными к ней внешними силами мы заменим внутренними силами (рис. 1.3, б). Эти внутренние силы оказывают противодействие внешней нагрузке, приложенной к оставленной части тела.

Бесконечную систему внутренних сил по правилам теоретической механики с помощью известной теоремы Пуансо (1804 г.) можно привести к одной точке – к центру тяжести поперечного сечения. В результате мы получим главный вектор Rи главный момент M (рис. 1.3, в).Разложим их на составляющие по осям x, y и z. Заметим, что оси x и y представляют собой главные оси, проходящие через центр тяжести поперечного сечения (подробнее см. беседу 4).

В итоге мы получим шесть внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы (рис. 1.3, г) и три момента (рис. 1.3, д).

Сила N называется продольной силой, – поперечными (или перерезывающими) силами, момент относительно оси z – крутящим моментом, моменты относительно осей x, y – изгибающими моментами.

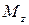
Необходимо отметить, что внутренние силовые факторы – векторные величины, составляющие главного вектора R и главного момента M по осям координат. Поэтому ошибочно говорить, например, что продольная сила N является проекцией главного вектора R на ось стержня, поскольку проекция вектора – это скалярная, а не векторная величина.

Как мы уже отмечали выше,разрушение тела не произойдет только в том случае, если эти шесть внутренних усилий сумеют уравновесить внешнюю нагрузку, действующую на рассматриваемую нами часть стержня.

Поэтому уравновесим оставленную нами часть стержня.

Записываем уравнения равновесия:

.

Из этих уравнений и определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.

При этом оказывается, что:

· продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;

· поперечные силы равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y соответственно;

· крутящий момент 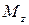равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z;

· изгибающие моменты равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y соответственно.

1.11. Что называется напряжением в точке тела на данной площадке? В каких единицах оно измеряется?

Очевидно, что в общем случае нагружения внутренние силы в стержне распределены и по его длине, и по его поперечному сечению неравномерно. Для суждения об интенсивности внутренних сил, возникающих, например, в некоторой точке поперечного сечения стержня, вводится понятие о напряжении в этой точке. Это понятие является ключевым понятием в сопротивлении материалов.

Напряжением в точке тела K (обозначим его буквой p) называется интенсивность внутренней силы , возникающей на бесконечно малой площадке в окрестности данной точки (рис. 1.4, а).

В количественном выражениинапряжение, возникающее в точке тела на площадке ,равно:

.

Заметим, что приведенное выражение, конечно же, неправомерно рассматривать как процедуру дифференцирования, при которой роль аргумента играет площадь поперечного сечения.

Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, которое действует, например, внутри жидкости. В технике под термином «давление» понимают величину, численно равную силе, действующей на единицу поверхности. Однако, хотя эти два понятия и сопоставимы, необходимо отметить следующее. Согласно закону Блеза Паскаля (Paskal, 1623 – 1662 гг.), давление в точке жидкости одинаково во всех направлениях. Если же мы проведем через точку K твердого тела другое сечение, то в новый разрез попадет другая пружинка и иной в общем случае будет и внутренняя сила. Следовательно, иным будет и напряжение, хотя оно и возникает в той же самой точке K.

Таким образом, при произвольном приложении внешней нагрузки напряжения, возникающие в некоторой точке тела на разных площадках, проходящих через данную точку, отличаются друг от друга.

Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши (Cauchy,1789 – 1857 гг.).

В дальнейшем мы увидим, что основную роль в расчетах прочности конструкций играет не полное напряжение p, а его составляющие на оси координат x, y и z: нормальное напряжение( – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения ( – тау), лежащие в плоскости сечения и направленные соответственно вдоль осей x и y (рис. 1.4, б). Первый индекс z у касательных напряжений характеризует нормаль к площадке, на которой они возникают.

Заметим, что иногда касательные напряжения называются тангенциальными напряжениями (от латинского слова tangens – касающийся) или скалывающими.

Между полным , нормальным и касательными напряжениями и существует следующая очевидная зависимость:

.

Отметим, что касательные напряжения служат мерой тенденции одной части сечения смещаться относительно другой его части.

Единица измерения нормальных и касательных напряжений в системе СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная приблизительно весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения очень мала. В сопротивлении материалов чаще используются другие единицы:

1 МПа = 10 6 Па; 1 кН/см 2 » 10 7 Па = 10 МПа.

В заключение необходимо отметить следующее. Ведя речь о напряжениях или о внутренних силовых факторах, мы не рекомендуем говорить, что они действуютв поперечном (или в некотором другом) сечении стержня, как поступают авторы некоторых учебниках по сопротивлению материалов. Правильнее говорить, что они возникают в рассматриваемом сечении стержня, поскольку при деформировании стержня и напряжения, и внутренние силовые факторы противодействуют внешней нагрузке, то есть они не играют активной роли. В крайнем случае слово «действуют» следует употреблять, заключая егов кавычки.

Наконец, еще раз подчеркнем, что нельзя говорить о напряжении в данной точке тела, не указывая положения площадки, на которой оно возникает.

1.12. Тогда еще один вопрос. Бесконечную систему внутренних сил, которая возникает в поперечном сечении стержня, мы приводим к центру тяжести сечения. В результате получаем так называемые главный вектори главный момент. Но почему мы здесь используем слово «главный»?

Эти старые термины, конечно же, неудачны и могут дезориентировать студента. Они возникли в результате неверного перевода французского слова «generale», обозначающего «общий», а вовсе не «главный». Эти термины имеют слишком большой «стаж». Они закрепились в великом множестве изданных книг и стали уже традиционными.

1.13. И последний вопрос. Почему в некоторых учебниках по сопротивлению материалов для обозначения тела, у которого один размер значительно превышает два других его размера помимо термина «стержень» часто используются и такие, например, слова, как «балка», «вал», «стойка» и «брус»?

Нам кажется, что термин «стержень» наиболее универсален. Он может употребляться при любом виде деформации. Термин «балка» следует использовать только в том случае, когда речь идет об изгибе стержня, «вал» – при его кручении, «стойка» – в задачах устойчивости стержня. Термин «брус» представляется нам не очень удачным. Этот термин – из лексикона строительного дела, в частности, он используется в специальном курсе деревянных конструкций.

РАСТЯЖЕНИЕ И СЖАТИЕ

Растяжение и сжатие – это наиболее простой и часто встречающийся вид деформации, поэтому именно с этой темы мы и продолжим нашу беседу. На растяжение (сжатие) работают многие элементы конструкций: стержни ферм, колонны, канаты лебедок, штоки паровых машин и др.

2.1. Какой вид деформации называется растяжением (сжатием)? Какие внутренние усилия возникают в поперечных сечениях стержня при растяжении (сжатии)?

Растяжением (сжатием) называется такой вид деформации стержня, при котором происходит изменение его первоначальной длины.

Растяжение (сжатие) стержня вызывается внешними силами, действующими вдоль его оси z, проходящей через центр тяжести поперечного сечения. При этом в любом поперечном сечении стержня возникает только одно внутреннее усилие – продольная сила N, которая является равнодействующей всех внутренних сил, возникающих в каждой точке этого поперечного сечения и направленных параллельно оси стержня.

2.2. Что называется эпюрой продольных сил и с какой целью она строится?

В тех случаях, когда продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика , называемого эпюрой продольных сил N. Эта эпюра наглядно демонстрирует нам, какие участки стержня испытываю растяжение, а какие – сжатие. При этом продольную силу N, противодействующую растяжению стержня, принято считать положительной, а сжатию – отрицательной.Эпюра N необходима для оценки прочности стержня. По этой эпюре определяется опасное сечение стержня. Как правило, это то его поперечное сечение, в котором продольная сила принимает наибольшее по абсолютной величине значение.

Построение эпюры N производится с помощью рассмотренного нами выше метода сечений. Продемонстрируем его применение на следующем примере (рис. 2.1).

Мы покажем, как определяется продольная сила N только в одном, намеченном нами поперечном сечении (рис. 2.1, а). В других поперечных сечениях стержня она может быть определена по аналогии.

Прежде всего, нам необходимо найти опорную реакцию R
(рис. 2.1, б), возникающую в заделке. Направим ее, например, вверх.

Составим уравнение равновесия 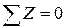для всего стержня:

.

Отсюда находим, что

кН.

Знак «плюс» в полученном результате говорит о том, что предварительное направление опорной реакции вверх было выбрано нами верно.

Разрежем теперьстержень по намеченному сечению и мысленно отбросим его нижнюю часть. Действие отброшенной части стержня нам необходимо заменить продольной силой N. Это мы можем осуществить следующими двумя способами.

Первый способ –будемвсегданаправлять продольную силу N от сечения, то есть будем предполагать, что она противодействует растяжению стержня. В этом случае положительный результат, полученный после уравновешивания оставленной части стержня, укажет нам на то, что внутренняя сила действительно соответствует растяжению, а отрицательный – что она противодействует сжатию.

По существу, первый способ является формальным.

Второй способ – будем направлять продольную силу, согласно здравому смыслу. То есть будем ориентироваться на значения внешних сил, действующих на рассматриваемую часть стержня, и помнить о том, что сила N должна их уравновесить. Тогда знак «плюс» в решении покажет, «угадали» или «не угадали» мы истинное направление продольной силы.

Проиллюстрируем первый способ. Направим, не задумываясь, внутреннюю силу N от сечения (рис. 2.1, в).

Для удобства вычисления значения продольной силы N закроем отброшеннуюнаминижнюю часть стержня, например листком бумаги. Разрушение стержня в рассматриваемом нами поперечном сечении не произойдет в том случае, если внутреннее усилие N уравновесит внешние силы R и , то есть те силы, которые мы видим. Записываем уравнение равновесия:

кН. (2.1)

Знак «минус» в полученном результате говорит нам о том, что в рассматриваемом сечении возникает продольное усилие N, противодействующее сжатию стержня.

Аналогичный результат мы получим и при отбрасывании верхней части стержня. Убедимся в этом, воспользовавшись теперь (для иллюстрации) вторым способом. Закром верхнюю часть стержня листком бумаги. Мы увидим, что внешняя сила кН растягивает, а сила кН сжимает нижнюю часть стержня. Продольное усилие N, возникающее в рассматриваемом нами поперечном сечении стержня, должно уравновесить эти две силы. Поскольку , сила N должна быть направлена к сечению стержня, то есть противодействовать сжатию. Тогда

кН.

С учетом принятого выше правила знаков, на эпюре продольных сил найденное значение N должно быть отложено со знаком «минус».

Таким образом, мы получили тот же самый результат.

2.3. По какому правилу осуществляется вычисление продольной силы N в произвольном поперечном сечении стержня?

Правило это очень простое: для определения продольной силы N, возникающей в некотором поперечном сечении стержня, необходимо найтиалгебраическую сумму всех внешних сил (активных и реактивных), действующих на любую из рассматриваемых частей стержня.

Если принято решение воспользоваться первым, формальным способом, то, складывая эти внешние силы, следует применить следующее правило знаков: силы, вызывающие растяжение рассматриваемойчасти стержня, включаются в упомянутую алгебраическую сумму со знаком «плюс», а силы, вызывающие сжатие, – со знаком «минус» (см. выражение (2.1)).

Второй способ представляется автору все же более целесообразным. В этом случае студент просто вынужден при определении продольной силы и построении эпюры N задумываться о виде деформации стержня (растянут он или сжат в рассматриваемом поперечном сечении).

2.4. В чем заключается смысл гипотезы плоских сечений?

Многочисленные эксперименты показывают, что при растяжении стержня продольные и поперечные риски, нанесенные на его поверхности до деформации, остаются практически прямолинейными и взаимно перпендикулярными между собой и после деформации стержня. Изменяются лишь расстояния между ними. Причем между поперечными рисками расстояния увеличиваются, а между продольными – уменьшаются.

Можно предположить, что и внутри стержня деформации имеют такой же характер, как и на его поверхности. Следовательно, поперечные сечения, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации. В этом и заключается смысл гипотезы плоских сечений, предложенной итальянским ученым Яковом Бернулли (Bernoulli,1654 – 1705 гг.).

Источник