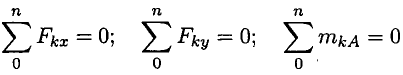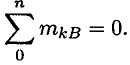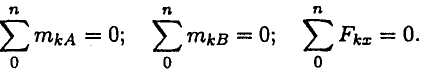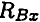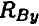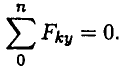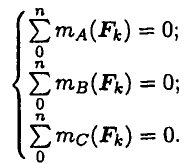нагрузки по способу приложения
НАГРУЗКИ ПО СПОСОБУ ПРИЛОЖЕНИЯ
По способу приложения нагрузки бывают объемными (собственный вес, силы инерции), действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные нагрузки и распределенные нагрузки.
В сопромате часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно q и выражаемой в ньютонах на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м, кгс/см) и т.д.
НАГРУЗКИ ПО ХАРАКТЕРУ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ
Вопрос
1. Брус — любое тело, у которого длина значительно больше других размеров.
В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев:
— прямой брус постоянного поперечного сечения (рис. 4.4, а);
— прямой ступенчатый брус (рис. 4.4, 6);
— криволинейный брус (рис. 4.4, в).
2. Пластина — любое тело, у которого толщина значительноменьше других размеров (рис.4.5).
3. Массив — тело, у которого три размера одного порядка.
Вопрос
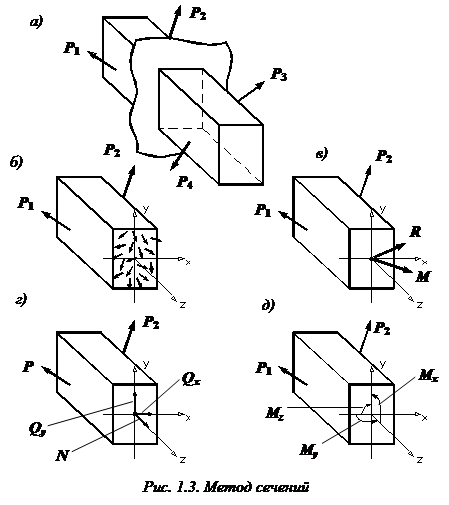
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
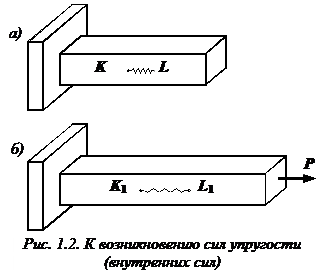
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
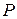
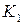
ВНУТРЕННИЕ СИЛЫ В МЕТОДЕ СЕЧЕНИЙ
Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).
Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.
Получим 6 внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы 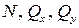

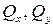
момент относительно оси z ( 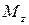
моменты относительно осей x, y ( 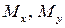
Запишем для оставленной части тела уравнения равновесия (уравновесим):
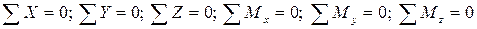
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.
Вопрос
Переменное напряжение
Напряжения, переменные во времени, возникающие в элементах конструкции под действием нагрузок, переменных по величине или направлению, а также нагрузок, перемещающихся относительно рассматриваемого элемента.
Допускаемое напряжение
Экспериментально установленное для рассматриваемого материала предельное значение напряжения, деленное на коэффициент запаса прочности.
Главное напряжение
Среди множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки и возникающие на них нормальные напряжения называются главными.
Классификация внешних сил (нагрузок)
Классификация Внешних Сил (Нагрузок) Сопромат
Внешние силы в сопромате делятся на активные и реактивные (реакции связей).Нагрузки – это активные внешние силы.
Нагрузки по способу приложения
По способу приложения нагрузки бывают объемными (собственный вес, силы инерции), действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные нагрузки и распределенные нагрузки.
В сопромате часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно q и выражаемой в ньютонах на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м, кгс/см) и т.д.
Нагрузки по характеру изменения во времени
Допущения сопромата
Допущения Сопромата Сопромат
При построении теории расчета на прочность, жесткость и устойчивостьпринимаются допущения, связанные со свойствами материалов и с деформацией тела.
Допущения, связанные со свойствами материалов
Сначала рассмотрим допущения, связанные со свойствами материалов:
допущение 1: материал считается однородным (его физико-механические свойства считаются одинаковыми во всех точках;
допущение 2: материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда). Это допущение дает возможность применять при исследовании напряженно-деформированного состояния тела методы дифференциального и интегрального исчислений, которые требуют непрерывности функции в каждой точке объема тела;
допущение 3: материал изотропный, то есть его физико-механические свойства в каждой точке одинаковы во всех направлениях. Анизотропные материалы – физико-механические свойства которых изменяются в зависимости от направления (например, дерево);
допущение 4: материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают).
Допущения, связанные с деформацией
Теперь рассмотрим основные допущения, связанные с деформацией тела.
допущение 1: деформации считаются малыми. Из этого допущения следует, что при составлении уравнений равновесия, а также при определении внутренних сил можно не учитывать деформацию тела. Это допущение иногда называют принципом начальных размеров. Например, рассмотрим стержень, заделанный одним концом в стену и нагруженный на свободном конце сосредоточенной силой (рис. 1.1).
допущение 2: перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (тело является линейно деформируемым). Для линейно деформируемых конструкций справедлив принцип независимости действия сил (принцип суперпозиции): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности. В основе этого принципа лежит также предположение об обратимости процессов нагрузки и разгрузки.
iSopromat.ru
Все внешние силы (нагрузки), действующие на изучаемое тело, следует рассматривать как проявление взаимодействия его с окружающими телами, которое представляется в виде сил или пар сил (моментов).
Все внешние силы (нагрузки) могут рассматриваться как сосредоточенные или распределённые.
В природе сосредоточенных сил не бывает. Все реальные тела практически контактируют через небольшие площадки. Однако принцип Сен-Венана позволяет распределенную нагрузку заменить равнодействующей силой, что упрощает расчёт.
Сосредоточенные нагрузки выражаются в ньютонах [H] и обозначается буквой F.
Распределённые нагрузки обозначаются буквой q и они бывают:
Сосредоточенные и распределённые нагрузки могут быть как статическими, так и динамическими.
Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.
Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут многократно превосходить те же нагрузки, приложенные статически.
Законы изменения нагрузок во времени могут иметь весьма сложный характер.
В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.
Классификация внешних нагрузок
Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками.
По способу приложения нагрузки бывают объемные и поверхностные, распределенные и сосредоточенные, по характеру изменения в процессе приложения – статические, динамические и повторно-переменные, по продолжительности действия – постоянные и временные.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Черчение
Классификация нагрузок
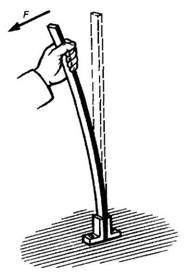
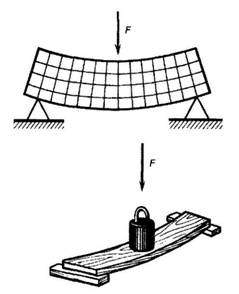
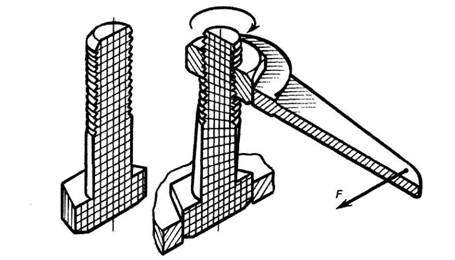
Воздействия, испытываемые стойкой от согнувшей ее руки (см. рис. 42), доской от груза (см. рис. 44), цилиндрическим стержнем болта при навинчивании гайки гаечным ключом (см. рис. 45) и т. д., представляют собой внешние силы или нагрузки. Силы, возникающие в местах закрепления стойки и опирания доски, называются реакциями.
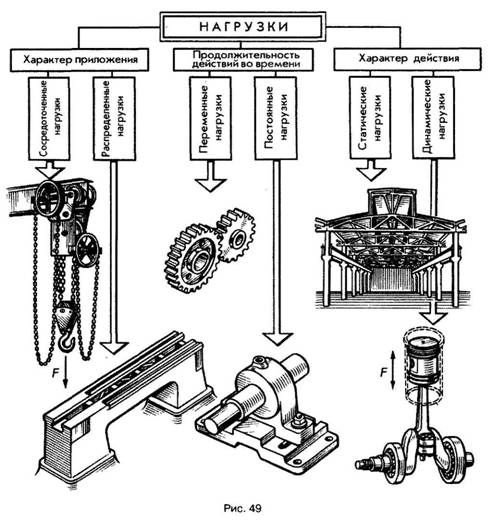
По способу приложения нагрузки делятся на сосредоточенные и распределенные (рис. 49).
Виды и классификация нагрузок:
Сосредоточенные нагрузки передают свое действие через,очень малые площади. Примерами таких нагрузок могут служить давление колес железнодорожного вагона на рельсы, давление тележки тали на монорельс и т. д.
Распределенные нагрузки действуют на сравнительно большой площади. Например, вес станка передается через станину на всю площадь соприкосновения с фундаментом.
По продолжительности действия принято различать постоянные и переменные нагрузки. Примером постоянной нагрузки может служить давление подшипника скольжения — опоры валов и осей — и его собственный вес на кронштейн.
Переменной нагрузке подвержены в основном детали механизмов периодического действия. Одним из таких механизмов служит зубчатая передача, у которой зубья в зоне контакта смежных пар зубчатых колес испытывают переменную нагрузку.
По характеру действия нагрузки могут быть статическими и динамическими. Статические нагрузки почти не изменяются в течение всего времени работы конструкции (например, давление ферм на опоры).
Динамические нагрузки действуют непродолжительное время. Их возникновение связано в большинстве случаев с наличием значительных ускорений и сил инерции.
Динамические нагрузки испытывают детали машин ударного действия, таких, как прессы, молоты и т. д. Детали кривошипно-шатунных механизмов также испытывают во время работы значительные динамические нагрузки от изменения величины и направления скоростей, то есть наличия ускорений.
Виды нагрузок и разновидности опор
Виды нагрузок и разновидности опор
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
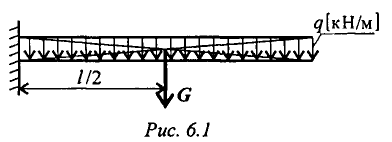
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).
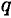
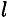
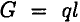
Разновидности опор балочных систем
Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.
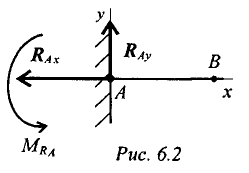
Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис. 6.2)
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы 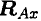
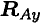
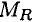
Для определения этих неизвестных удобно использовать систему уравнений в виде
Каждое уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например 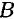
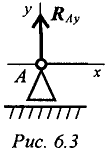
Шарнирно-подвижная опора (рис. 6.3)
Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
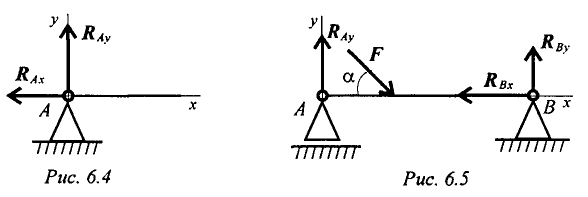
Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
Балка на двух шарнирных опорах (рис. 6.5)
Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме
Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.
Из уравнения 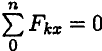
Из уравнения 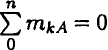
Из уравнения 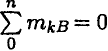
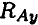
Для контроля правильности решения используется дополнительное уравнение
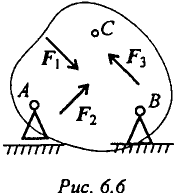
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института