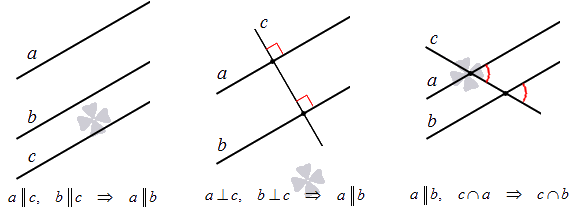Как записать что точка лежит на прямой

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Обозначение прямой

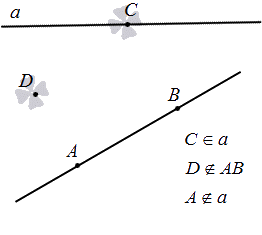
Например, на рисунке 1 обозначены такие прямые:

Рис. 1 Обозначение прямой линии

Рис. 2 Обозначение прямой с несколькими точками

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

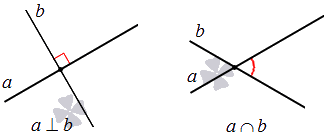
Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

Рис. 5 Пересечение прямых

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

Луч имеет второе название – полупрямая.

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 22

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Прямая линия

Прямая линия — это линия, не имеющая неровностей, скруглений и углов. Прямая линия бесконечна, она не имеет ни начала, ни конца. В геометрии прямая линия называется просто прямой.

Для изображения прямой на бумаге используется линейка. Чтобы начертить прямую, надо провести черту вдоль края линейки:

Так как прямая бесконечна, то какой бы длины не была проведена черта, она будет изображать только часть прямой.

Обозначение прямой

Прямая обозначается одной маленькой латинской буквой, например прямая a, или двумя большими латинскими буквами, поставленными при любых двух точках, лежащих на этой прямой, например прямая AB:

Обратите внимание, что точки на прямой можно обозначать короткими чёрточками.

Свойства прямой

1. Через любые две точки можно провести только одну прямую линию.

Это основное свойство прямой. Оно часто используется на практике, для прокладывания прямых линий с помощью двух каких-либо объектов.

2. Если две любые точки прямой лежат на плоскости, то все точки этой прямой лежат на той же плоскости.

3. Через одну точку можно провести бесконечно много прямых.

4. Есть точки лежащие на прямой и не лежащие на ней.

Точки N и M лежат на прямой a. Точка L не лежит на прямой a.

5. Из трёх разных точек, лежащих на одной прямой, только одна может лежать между двумя другими точками.

На рисунке изображена прямая с тремя точками A, B и C, лежащими на ней. Про эти точки можно сказать:

точка B лежит между точками A и C, точка B разделяет точки A и C

Также можно сказать:

точки B и C лежат по одну сторону от точки A, они не разделяются точкой A

6. Две прямые, лежащие на одной плоскости, или пересекаются друг с другом в одной точке, или являются параллельными.

Источник

Прямая на плоскости – необходимые сведения.

В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.

Навигация по странице.

Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).

Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости.

Теперь можно переходить и к понятию прямой линии на плоскости.

Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.

Взаимное расположение прямой и точки.

Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.

Возможны два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).

Справедливо следующее утверждение: через любые две точки проходит единственная прямая.

Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В ), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА ).

Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

Взаимное расположение прямых на плоскости.

Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?

Во-первых, две прямые на плоскости могут совпадать.

Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.

Во-вторых, две прямые на плоскости могут пересекаться.

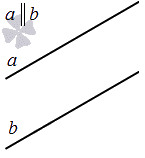
В-третьих, две прямые на плоскости могут быть параллельными.

Две прямые на плоскости называются параллельными, если они не имеют общих точек. Если прямая a параллельна прямой b, то используют символическое обозначение . Для более полной информации смотрите статью параллельные прямые, параллельность прямых.

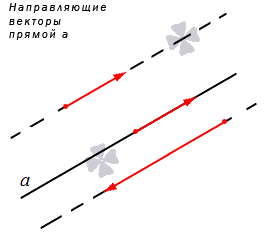
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой. В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.

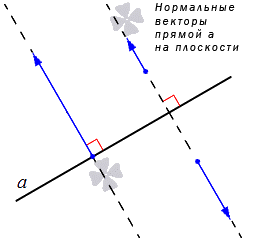
Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой. О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости.

Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.

Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:

Способы задания прямой на плоскости.

Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.

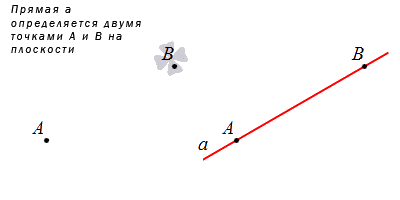
Во-первых, прямую можно задать, указав две точки на плоскости.

Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.

Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки.

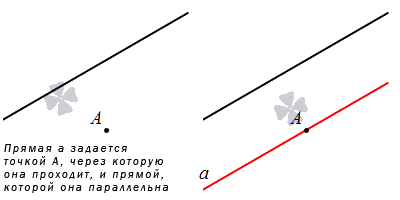
Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.

Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение. Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой.

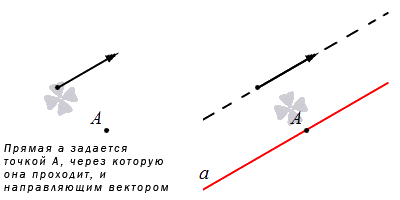
В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.

Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости.

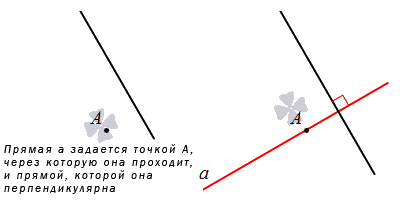
Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.

Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.

Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой.

Источник

Прямая на плоскости – необходимые сведения

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

На каждой прямой и в каждой плоскости могут быть отмечены точки.

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

Две прямые на плоскости могут пересекаться.

Две прямые на плоскости могут быть параллельны.

Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

Источник