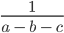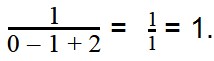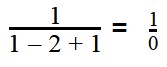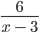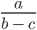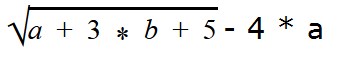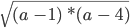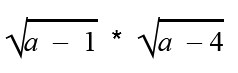Как понять что выражение имеет смысл

Числовые и алгебраические выражения. Преобразование выражений.

Что такое выражение в математике? Зачем нужны преобразования выражений?

Допустим, перед вами злой пример. Очень большой и очень сложный. Допустим, вы сильны в математике и ничего не боитесь! Сможете сразу дать ответ?

Вам придётся решать этот пример. Последовательно, шаг за шагом, этот пример упрощать. По определённым правилам, естественно. Т.е. делать преобразование выражений. Насколько успешно вы проведёте эти преобразования, настолько вы и сильны в математике. Если вы не умеете делать правильные преобразования, в математике вы не сможете сделать ни-че-го.

Во избежание такого неуютного будущего (или настоящего. ), не мешает разобраться в этой теме.)

Для начала выясним, что такое выражение в математике. Что такое числовое выражение и что такое алгебраическое выражение.

Что такое выражение в математике?

В общем виде термин «математическое выражение» применяется, чаще всего, чтобы не мычать. Спросят вас, что такое обыкновенная дробь, например? И как ответить?!

Первый вариант ответа: «Это. м-м-м-м. такая штука. в которой. А можно я лучше напишу дробь? Вам какую?»

Второй вариант как-то посолидней будет, правда?)

Вот в этих целях фраза «математическое выражение» очень хороша. И правильно, и солидно. Но для практического применения надо хорошо разбираться в конкретных видах выражений в математике.

Числовые выражения.

Что такое числовое выражение? Это очень простое понятие. Само название намекает, что это выражение с числами. Да, так оно и есть. Математическое выражение, составленное из чисел, скобок и знаков арифметических действий называется числовым выражением.

тоже числовое выражение, да.

Когда числовое выражение не имеет смысла?

Понятное дело, если мы видим перед собой какую-то абракадабру, типа

то делать ничего и не будем. Так как непонятно, что с этим делать. Бессмыслица какая-то. Разве что, посчитать количество плюсиков.

Но бывают внешне вполне благопристойные выражения. Например такое:

Чтобы дать такой ответ, пришлось, конечно, посчитать, что в скобочках будет. А иногда в скобочках такого понаворочено. Ну тут уж ничего не поделаешь.

Алгебраические выражения.

и так далее, до бесконечности. )

В арифметике можно записать, что

А вот если мы подобное равенство запишем через алгебраические выражения:

мы сразу решим все вопросы. Для всех чисел махом. Для всего бесконечного количества. Потому, что под буквами а и b подразумеваются все числа. И не только числа, но даже и другие математические выражения. Вот так работает алгебра.

Когда алгебраическое выражение не имеет смысла?

Про числовое выражение всё понятно. Там на ноль делить нельзя. А с буквами, разве можно узнать, на что делим?!

Возьмём для примера вот такое выражение с переменными:

Конечно. Просто в таких случаях говорят, что выражение

имеет смысл для любых значений а, кроме а = 5.

Весь набор чисел, которые можно подставлять в заданное выражение, называется областью допустимых значений этого выражения.

Как видите, ничего хитрого нет. Смотрим на выражение с переменными, да соображаем: при каком значении переменной получается запретная операция (деление на ноль)?

А потом обязательно смотрим на вопрос задания. Чего спрашивают-то?

Если спрашивают, при каком значении переменной выражение не имеет смысла, наше запретное значение и будет ответом.

Если спрашивают, при каком значении переменной выражение имеет смысл (почувствуйте разницу!), ответом будут все остальные числа, кроме запретного.

Зачем нам смысл выражения? Есть он, нет его. Какая разница?! Дело в том, что это понятие становится очень важным в старших классах. Крайне важным! Это основа для таких солидных понятий, как область допустимых значений или область определения функции. Без этого вы вообще не сможете решать серьёзные уравнения или неравенства. Вот так.

Преобразование выражений. Тождественные преобразования.

Мы познакомились с числовыми и алгебраическими выражениями. Поняли, что означает фраза «выражение не имеет смысла». Теперь надо разобраться, что такое преобразование выражений. Ответ прост, до безобразия.) Это любое действие с выражением. И всё. Вы эти преобразования делали с первого класса.

Возьмём крутое числовое выражение 3+5. Как его можно преобразовать? Да очень просто! Посчитать:

Вот этот расчёт и будет преобразованием выражения. Можно записать то же самое выражение по-другому:

Тут мы вообще ничего не считали. Просто записали выражение в другом виде. Это тоже будет преобразованием выражения. Можно записать вот так:

Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто. Но есть здесь одно очень важное правило. Настолько важное, что его смело можно назвать главным правилом всей математики. Нарушение этого правила неизбежно приводит к ошибкам. Вникаем?)

Предположим, мы преобразовали наше выражение как попало, вот так:

Преобразование? Конечно. Мы же записали выражение в другом виде, что здесь не так?

Всё не так.) Дело в том, что преобразования «как попало» математику не интересуют вообще.) Вся математика построена на преобразованиях, в которых меняется внешний вид, но суть выражения не меняется. Три плюс пять можно записать в каком угодно виде, но это должно быть восемь.

Преобразования, не меняющие сути выражения называются тождественными.

Именно тождественные преобразования и позволяют нам, шаг за шагом, превращать сложный пример в простое выражение, сохраняя суть примера. Если в цепочке преобразований мы ошибёмся, сделаем НЕ тождественное преобразование, дальше мы будем решать уже другой пример. С другими ответами, которые не имеют отношения к правильным.)

Вот оно и главное правило решения любых заданий: соблюдение тождественности преобразований.

Пример с числовыми выражением 3+5 я привёл для наглядности. В алгебраических выражениях тождественные преобразования даются формулами и правилами. Скажем, в алгебре есть формула:

Как вы, наверняка, догадались, эту цепочку можно продолжать до бесконечности. ) Очень важное свойство. Именно оно позволяет превращать всякие монстры-примеры в белые и пушистые.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Область допустимых значений функции

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 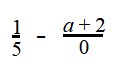— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

Рассмотрим каждый случай в отдельности.

Пример 7

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Источник

Фразеологизм

3 класс, 6 класс, 10 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение фразеологизма

В лексике русского языка есть не только отдельные слова, которые помогают описывать окружающую действительность, но и словосочетания, которые называют фразеологизмами. Например:

На примерах видно, что значение фразеологизма не связано с семантикой каждого отдельного слова в его составе. Компоненты фразеологизма теряют все самостоятельные признаки слова, кроме звукового облика: лексическое значение, формы изменения, синтаксическую функцию. Связь между словами в составе фразеологизма тесная, можно сказать — неразделимая.

Фразеологизмы — это устойчивые выражения из двух и более слов. Они отлично живут в нашей культуре, при этом их невозможно дословно перевести на другие языки — для иностранца такой перевод будет звучать странно и непонятно.

Виды фразеологизмов в русском языке

Выделяют три основных вида фразеологизмов: идиомы, фразеологические единства и фразеологические сочетания.

Фразеологические сращения (идиомы) — устойчивые выражения, которые имеют смысл только в неизменном виде. При замене или перестановке слов смысл идиомы потеряется. Например: «бить баклуши», то есть бездельничать.

Фразеологические единства — устойчивые образные выражения, смысл которых понятен из смысла отдельных слов. Например, обороты «грызть гранит науки» или «попасться на удочку» можно понять даже при переводе на другой язык. Смысл фразеологического единства не потеряется, если заменить «удочку» на «крючок» или вставить в оборот лишнее слово.

Фразеологические сочетания — устойчивые, но гибкие обороты, смысл которых определяется через отдельные ключевые слова. При этом не ключевые слова можно заменять синонимами. Пример: можно «умирать от любви», а можно «умирать от восторга» — смысл обоих словосочетаний понятен.

Приглашаем на увлекательные курсы изучения русского языка в онлайн-школу для детей и подростков Skysmart!

Признаки фразеологизмов

Как мы уже выяснили, фразеологизм — это устойчивое по составу и структуре образное выражение из двух и более слов. У фразеологизма как самостоятельной лексической единицы языка есть свои отличительные черты.

1. Фразеологизм состоит из двух и более слов

2. У фразеологизмов есть устойчивый состав

Лексический состав фразеологизма нельзя никак изменять, так как при этом теряется его смысл.

Для примера попробуем поменять слова в устойчивом выражении «висеть в воздухе», что значит «оказаться в неясном, неопределенном положении»:

В результате этого языкового эксперимента фразеологизм рассыпался, как карточный домик, из которого неосторожно вытащили одну карту. Глагол «висеть» потерял свое переносное значение, и смысл фразеологизма испарился.

3. Главный признак фразеологизмов — воспроизводимость

Мы не придумываем фразеологизмы в процессе диалога, а берем их из языковой памяти, как готовые кирпичики для построения образной и выразительной речи. Именно поэтому в школьные годы важно много читать, чтобы пополнять словарный и фразеологический запас.

В острог его посадят, например, — он попросит водицы испить в ковшике: ему принесут ковшик, а он нырнет туда, да и поминай как звали (И. Тургенев).

Но случай сей произвел еще большее впечатление на Марью Кирилловну. Воображение ее было поражено: она видела мертвого медведя и Дефоржа, спокойно стоящего над ним и спокойно с нею разговаривающего. Она увидела, что храбрость и самолюбие не исключительно принадлежат одному сословию, и с тех пор стала оказывать молодому учителю уважение, которое час от часу становилось внимательнее (А. Пушкин).

Я, Софья Павловна, день целый
Нет отдыха, мечусь как словно угорелый.
По должности, по службе хлопотня,
Тот пристает, другой, всем дело до меня! (А. Грибоедов)

Задачка: попробуйте понять, какие русские фразеологизмы изображены на картинках. Правильные ответы — в конце статьи.

4. Переносное значение фразеологизмов сложилось исторически

Иногда переносное значение фразеологизма нельзя понять, не обратившись к истории его возникновения.

Например, фразу «на козе не подъедешь» трудно понять, особенно иностранцам, которые изучают русский язык. На самом деле оно тесно связано с речью шутов и скоморохов, которые в старину веселили народ на ярмарках и праздниках, наряжаясь в козу, медведя и других персонажей. Но на особо важных и угрюмых людей даже эта уловка не действовала, с тех пор и говорят «на козе не подъедешь» о неприступных, гордых, важных людях.

5. Все слова одного фразеологизма — это один член предложения

Рассмотрим пример: «Сегодня мы (что делали?) работали до седьмого пота». Фразеологизм «работали до седьмого пота» выполняет роль сказуемого.

Фразеологизм может быть синонимом одному слову:

ставить точку в споре

Фразеологизмы делают нашу речь образной и живой, они помогают передать больше смысла и сделать это эмоционально и выразительно.

Примеры фразеологизмов с объяснением

Вот несколько примеров фразеологизмов, которые пришли к нам из древних мифов, и их значений в русском языке.

Источник

Числовые и буквенные выражения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

14 больше 4
14 > 4
6 + 8 > 2 * 2

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

Пример 1. Найдите значение выражения: 5 + x.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Источник