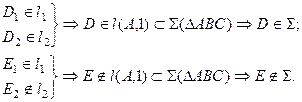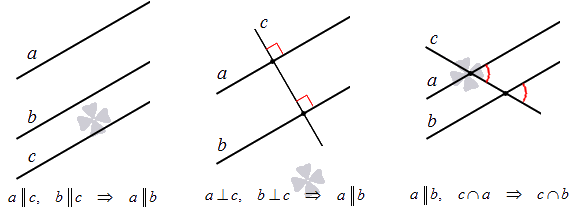Как понять что прямая принадлежит плоскости
Принадлежность прямой и точки плоскости



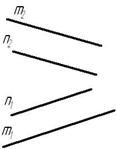
Рис. 3.2 Взаимное расположение прямых
Прямые в пространстве могут занимать относительно друг друга одно из трех положений:
1) быть параллельными;
Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.
Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).
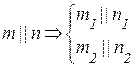
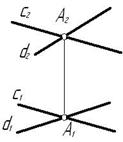
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная (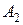
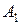
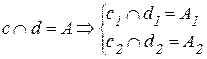
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.
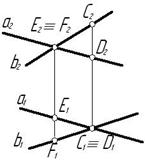
На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).
Признак принадлежности точки и прямой плоскости:
Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.
На рис. 3.5 изображена плоскость 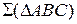
На рис. 3.6 показана плоскость 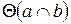
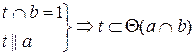
Как понять что прямая принадлежит плоскости
Сформулируем условие принадлежности прямой плоскости как аксиомы:
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.
Проиллюстрируем примерами использование этих аксиом.
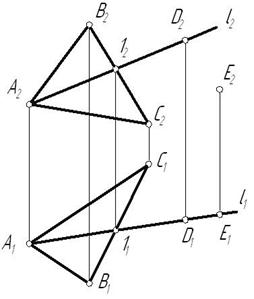
Требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.
Проекция прямой m2 пересекает проекции прямых n2 и k2 в точках В2 и С2 соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.
Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.
Рисунок 53. Прямая и плоскость имеют две общие точки
Задача. Через точку В провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис. 5 4).
Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k , значит согласно аксиоме 2 прямая принадлежит этой плоскости.
Прямая на плоскости – необходимые сведения
Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.
Прямая на плоскости – понятие
Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.
Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.
Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.
Взаимное расположение прямой и точки
На каждой прямой и в каждой плоскости могут быть отмечены точки.
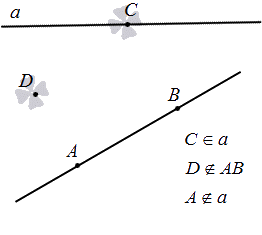
Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.
Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.
Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:
Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.
Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.
Точка делит прямую на две части, называемые лучами. Имеем аксиому:
Взаимное расположение прямых на плоскости
Расположение прямых на плоскости может принимать вид двух состояний.
Две прямые на плоскости могут совпадать.
Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.
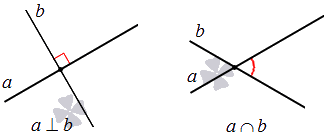
Две прямые на плоскости могут пересекаться.
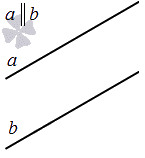
Две прямые на плоскости могут быть параллельны.
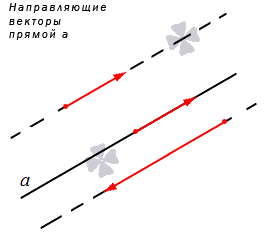
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.
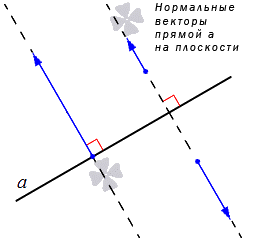
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.
Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.
Для этого приводим необходимы факторы, доказывающие их взаимное расположение:
Рассмотрим это на рисунках.
Способы задания прямой на плоскости
Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.
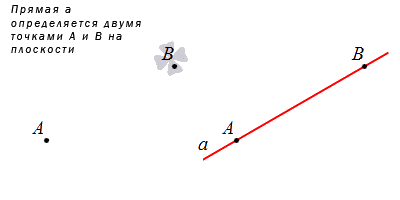
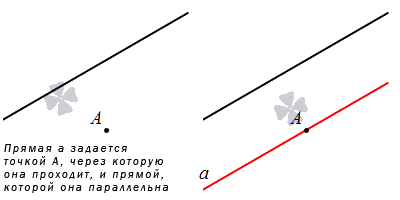
Прямая задается при помощи указанных двух точек, расположенных в плоскости.
Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.
Прямая может быть задана через точку и прямую, которой она параллельна.
Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.
Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.
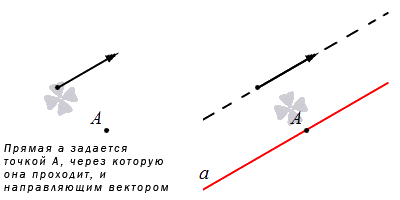
Прямая задается через указанную точку и направляющий вектор.
Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.
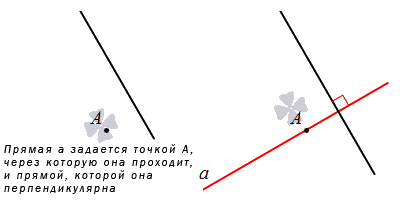
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:
Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.
И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.
Лекция 3. Плоскость
3.1. Способы задания плоскости на ортогональных чертежах
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).
Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).
Рисунок 3.5 – Принадлежность точки плоскости
Рисунок 3.6 – Принадлежность прямой плоскости
\left.\begin
Упражнение
Рисунок 3.7 – Решение задачи
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником
Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами
Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами
Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
\alpha=m\cap n\\\left.\begin
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
Рисунок 3.15 – Пересечение прямой с плоскостью
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.
Рисунок 3.17 – Построение плоскости, параллельной заданной
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Упражнение
Алгоритм решения задачи :
\left.\begin
KL – линия пересечения ΔАВС и σ (α∩σ = KL).
Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи :
\left.\begin
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.