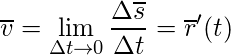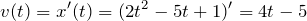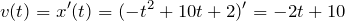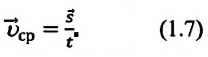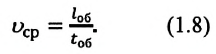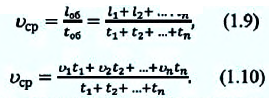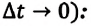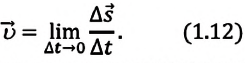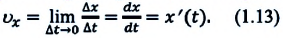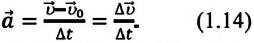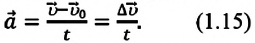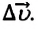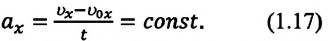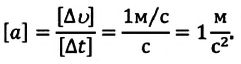Как определяется мгновенная скорость при прямолинейном движении чему равен ее модуль
Мгновенная скорость
Мгновенная скорость при прямолинейном движении материальной точки
При рассмотрении неравномерного движения часто интересует не средняя скорость движения тела, а скорость в определенный момент времени, или мгновенная скорость. Так, если тело стукнулось о препятствие, то сила воздействия тела на препятствие в момент удара, определено скоростью в момент соударения, а не средней скоростью движения тела. Форма траектории перемещения снаряда и его дальность полета зависит от скорости в момент запуска, а не от средней скорости.
\[\left\langle v\right\rangle =\frac<\Delta x><\Delta t>\left(1\right),\]
Мгновенную скорость определим как предел к которому стремится средняя скорость за бесконечно малый промежуток времени:
Такой предел в математике называют производной:
Мгновенная скорость равномерного движения материальной точки
Средняя скорость равномерно движущейся точки величина постоянная, значит, мгновенная скорость равномерно перемещающейся точки является неизменной величиной.
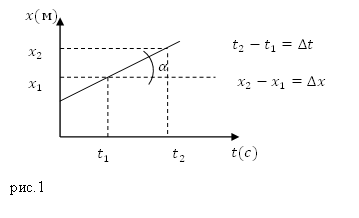
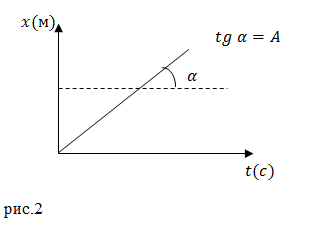
Скорость равномерного движения численно равна тангенсу угла наклона прямой к оси времени (рис.1):
\[v=k\ tg\ \alpha \ \left(4\right),\]
При графическом изображении переменного движения материальной точки мгновенная скорость численно равна тангенсу угла наклона касательной к графику и осью абсцисс.
Мгновенная скорость при криволинейном движении
Примеры задач с решением
Задание. Две материальные точки движутся согласно уравнениям:
в какой момент времени скорости этих точек будут равны?
Решение. В задаче речь идет о нахождении времени, когда будут равны мгновенные скорости материальных точек. Величину мгновенной скорости будем находить как:
Тогда подставляя по очереди уравнения из системы (1.1) получим:
Приравняем правые части уравнений в системе (1.3), найдем момент времени в который скорости равны ($v_1=v_2$):
\[-3+8t-3t^2=1-4t-3t^2\to 8t+4t=1+3\to 12t=4\to t=\frac<1><3>\left(c\right).\]
Получили, что движение материальной точки в плоскости XOY описывают при помощи системы уравнений:
Найдем составляющие скорости движения материальной точки:
Мгновенная скорость движения
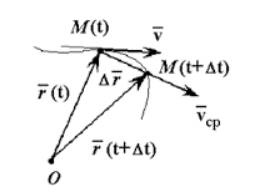
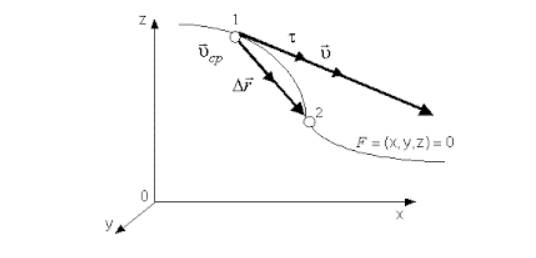
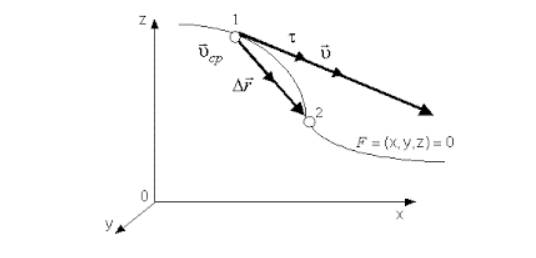
Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.
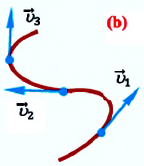
Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.
Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.
Имеет ли понятие «мгновенной скорости» физический смысл? Скорость – это характеристика изменения перемещения тела в пространстве. Однако, для того, чтобы определить, как изменилось перемещение, необходимо наблюдать за движением в течение некоторого времени. Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть достаточно малый 
Примеры решения задач по теме «Мгновенная скорость»
| Задание | О какой скорости – средней или мгновенной – идет речь в следующих случаях: |
1) самолет летит из Санкт-Петербурга в Москву со скоростью 800 км/ч;
2) пуля вылетает из винтовки со скоростью 800 м/с;
3) велосипедист едет по шоссе со скоростью 12 км/ч;
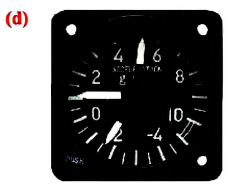
4) прибор показывает скорость тепловоза 75 км/ч?
2) и 4) – речь идет о мгновенной скорости.
| Задание | Закон движения точки по прямой задается уравнением 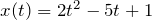 . Найти мгновенную скорость точки через 10 секунд после начала движения. . Найти мгновенную скорость точки через 10 секунд после начала движения. |
| Решение | Мгновенная скорость точки – это первая производная радиус-вектора по времени. Поэтому для мгновенной скорости можно записать: |
Через 10 секунд после начала движения мгновенная скорость будет иметь значение:
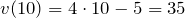
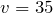 м/с.
м/с.| Задание | Тело движется по прямой так, что его координата 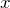 (в метрах) изменяется по закону (в метрах) изменяется по закону 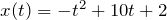 . Через сколько секунд после начала движения тело остановится? . Через сколько секунд после начала движения тело остановится? |
| Решение | Найдем мгновенную скорость тела: |
В момент остановки мгновенная скорость тела будет равна нулю:
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость » open=» υ при стремлении промежутка времени ∆ t к 0 :
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
Мгновенная скорость

Всего получено оценок: 214.
Всего получено оценок: 214.
Большинство движений в природе являются неравномерными. При описании таких движений большое значение имеет параметр «мгновенная скорость». Рассмотрим его подробнее.
Скорость при неравномерном движении
Скорость – величина, показывающая, какое расстояние проходит материальная точка за единицу времени:

Однако, для определения положения материальной точки в любой момент времени, во многих случаях эту формулу применять нельзя.
В самом деле, если провести опыт, можно видеть, что на Земле предмет падает с высоты 20м за 2.02с. Откуда следует, что скорость падения составляет:
Выходит, что через полсекунды после начала падения предмет окажется на 5м ниже, чем исходная точка, через секунду – на 9.9м ниже.
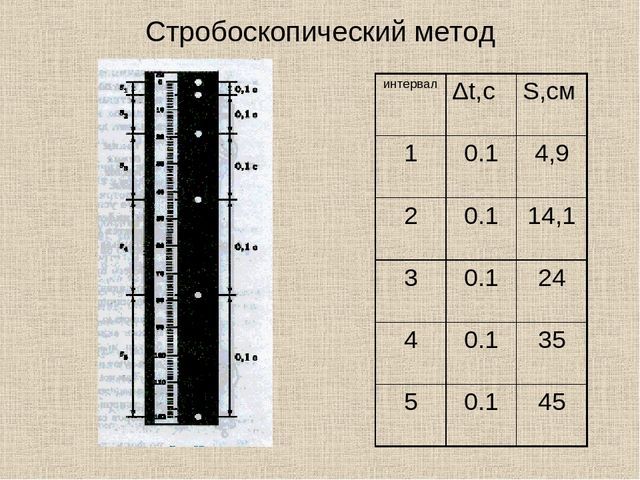
Причина такого расхождения с расчетом состоит в том, что предмет под действием тяготения Земли движется неравномерно, постоянно изменяя скорость. И на каком бы участке мы не измерили его скорость – полученное значение будет различно, и его невозможно будет использовать в расчетах и уравнениях для других участков.
Свести неравномерное движение к равномерному невозможно.
Мгновенная скорость
Описанное затруднение можно разрешить, если учесть, что движение – процесс непрерывный. Ни координаты точки, ни ее скорость не могут изменяться скачками. Во время движения точка проходит все бесчисленное множество координат пути, на всем пути скорость ее непрерывно изменяется в некотором диапазоне, и при этом, чем меньше рассматриваемый отрезок времени, тем меньше будет изменение координаты и скорости.
Рассмотрим падение предмета, начиная с конца первой секунды. В этот момент координата будет равна 4.905м. Отметим новую координату падающего предмета через небольшое время, и вычислим скорость:
Содержание:
Прямолинейное неравномерное движение, ускорение:
На практике прямолинейное равномерное движение наблюдается очень редко. Скорость движущегося автомобиля, поезда, самолета, частей механизма и т.д. может изменяться и по величине, и по направлению.
Прямолинейное движение, при котором за равные промежутки времени материальная точка совершает разные перемещения, называют прямолинейным неравномерным движением.
При таком движении числовое значение скорости не остается неизменным, поэтому для описания неравномерного движения пользуются понятиями средней и мгновенной скорости.
Средняя скорость
Средняя скорость неравномерно движущейся материальной точки на данном участке траектории равна отношению ее перемещения на этом участке ко времени совершения этого перемещения:
Средняя путевая скорость материальной точки при неравномерном движении равна отношению всего пройденного пути ко времени, затраченному на прохождение этого пути:
Средняя скорость материальной точки, движущейся со скоростями 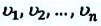
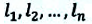
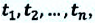
Если 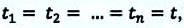
Мгновенная скорость.
Скорость материальной точки в данный момент времени или в данной точке траектории называют мгновенной скоростью.
Мгновенная скорость в некоторой точке является векторной величиной и определяется как предел отношения достаточно малого перемещения 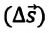
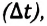
Где 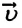
С течением времени мгновенная скорость может увеличиваться, уменьшаться и изменять направление. Направление мгновенной скорости в данной точке траектории совпадает с направлением касательной к траектории в этой точке (b). Проекция вектора мгновенной скорости в прямоугольной системе координат равна первой производной координаты по времени:
Ускорение
Быстрота изменения мгновенной скорости при неравномерном движении по величине и направлению характеризуется векторной физической величиной, называемой ускорением:
Если измерение времени начинается с нуля 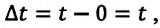
Направление ускорения совпадает с направлением вектора
Для простоты здесь и в последующем будет рассматриваться такое неравномерное прямолинейное движение материальной точки, при котором за любые равные промежутки времени происходит одинаковое изменение скорости. Такое движение называется равнопеременным движением.
Равнопеременное движение
При равнопеременном движении проекция ускорения на любую ось, например ось 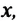
В СИ за единицу ускорения принят 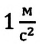
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.