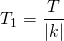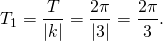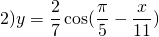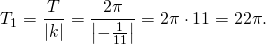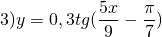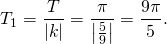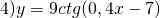Как определить что функция периодическая
Как определить периодичность функции
Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.
Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.
Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.
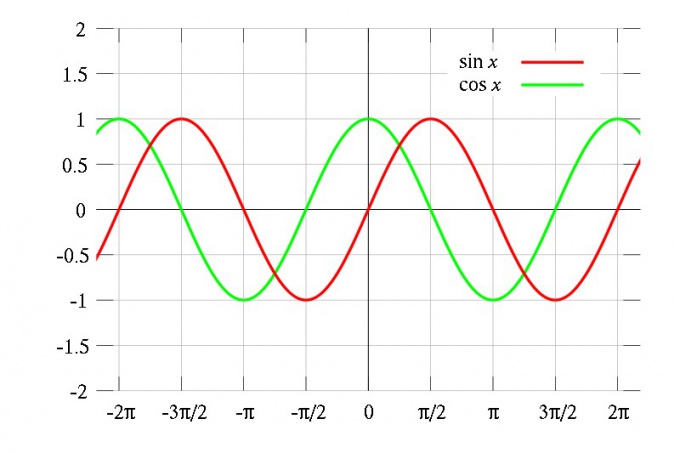
Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.
Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.
Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.
Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.
Периодические функции
С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.
Дадим определение периодической функции:
Например, — периодические функции.
Для функций и период
Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:
1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения
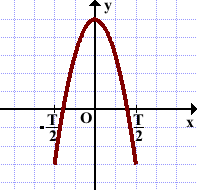
График функции может выглядеть, например, вот так:
Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.
2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).
Построим график функции при
Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.
Период функции равен 2. Повторим периодически участок длины 2, который уже построен.
3. Найдите наименьший положительный период функции
Наименьший положительный период функции равен
График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).
Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции
4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции
Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.
Периодическая функция
Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).
Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:
Число T называют периодом функции y=f(x).
Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).
Свойства периодических функций
1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).
2) Для любого x из области определения y=f(x) если T1 — период функции, то
Так как T2 также является периодом функции y=f(x), то для аргумента x-T1
Следовательно, число T1+T2 является периодом функции y=f(x).
3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.
4) Если T — период функции f(x), то для аргумента kx+b
Значит число T/k — период функции f(kx+b).
5) Эти свойства следуют непосредственно из определения.
Например, для суммы f(x) и g(x):
Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.
Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.
Примеры периодических функций
1) Поскольку для любого x выполняются равенства
то функции y=sin x и y=cos x являются периодическими с периодом T=2π.
2) Так как для любого x из области определения функции y=tg x выполняется равенство
tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.
Аналогично, y=ctg x — периодическая функция с периодом T=π.
3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.
Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.
4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.
Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.
Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.
5) Так как для любого действительного x и любого целого k выполняется равенство
Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=
Главный период функций y=sin x и y=cos x T=2π.
Главный период функций y=tg x и y=ctg x T=π.
Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.
То есть любой период функции y=sin x имеет вид 2πn, n∈Z.
Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.
Таким образом, 2π — главный период функции y=sin x.
Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.
Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период
а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период
График периодической функции повторяется через промежутки длиной T (на оси Ox).
Дана часть графика
промежутке длиной T.
Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :
А периодическая функция это функция который повторяет свои значения через равные промежутки времени, например, тригонометрические функции, которые повторяются с интервалом 2π радианы. Периодические функции используются в науке для описания колебания, волны, и другие явления, которые проявляют периодичность. Любая непериодическая функция называется апериодический.
Содержание
Определение
Примеры
Примеры вещественных чисел
Примеры повседневного использования можно увидеть, когда переменная время; например руки Часы или фазы Луна показывают периодическое поведение. Периодическое движение движение, в котором положение (я) системы выражается как периодические функции, все с одно и тоже период.
Для функции на действительные числа или на целые числа, это означает, что весь график могут быть сформированы из копий одной конкретной части, повторяющихся через равные промежутки времени.
Согласно приведенному выше определению, некоторые экзотические функции, например Функция Дирихле, также являются периодическими; в случае функции Дирихле любое ненулевое рациональное число является периодом.
Примеры комплексных чисел
С помощью комплексные переменные у нас есть функция общего периода:
Сложные функции могут быть периодическими вдоль одной линии или оси в комплексной плоскости, но не на другой. Например, е z < displaystyle e ^ 
Двойные периодические функции
Функция, доменом которой является сложные числа может иметь два несоизмеримых периода, не будучи постоянным. В эллиптические функции такие функции. («Несоизмеримые» в этом контексте означают, что они не кратны друг другу.)
Характеристики
Обобщения
Антипериодические функции
Одним из общих подмножеств периодических функций является подмножество антипериодические функции. Это функция ж такой, что ж(Икс + п) = −ж(Икс) для всех Икс. (Таким образом, п-антипериодической функцией является 2п-периодическая функция.) Например, функции синуса и косинуса являются π-антипериодическими и 2π-периодическими. Хотя п-антипериодической функцией является 2п-периодической функции, обратное не обязательно.
Блоховско-периодические функции
Дальнейшее обобщение появляется в контексте Теоремы Блоха и Теория Флоке, управляющие решением различных периодических дифференциальных уравнений. В этом контексте решение (в одном измерении) обычно является функцией формы:
Факторные пространства как домен
Расчетный период
Если не существует наименьшего общего знаменателя, например, если один из вышеуказанных элементов был иррациональным, тогда волна не была бы периодической. [2]
Узнать ещё
Знание — сила. Познавательная информация
Как найти период функции
Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции
где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.
Найти период функции:
Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции
А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то
А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции
А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть