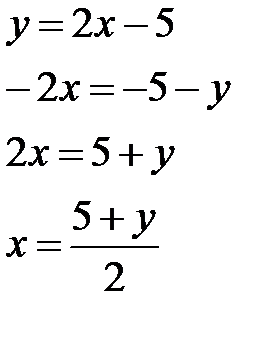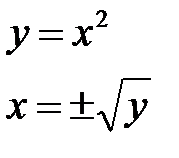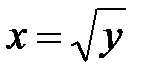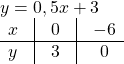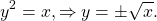Как определить что функция обратима
АЛГОРИТМ СОСТАВЛЕНИЯ ОБРАТНОЙ ФУНКЦИИ.
Лекция по теме «Обратная функция»
ПОНЯТИЕ ОБРАТИМОЙ ФУНКЦИИ.
ДОСТАТОЧНОЕ УСЛОВИЕ ОБРАТИМОСТИ.
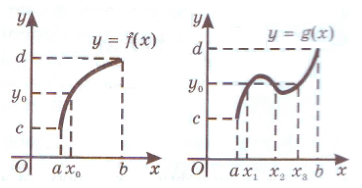
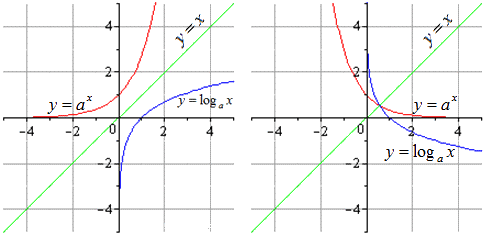
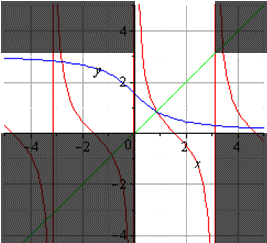
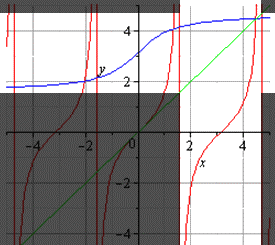
На рисунках приведены две функции, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет (рис.1). Таким образом, функция 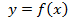
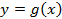
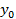
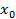
У функции 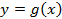
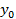
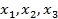
Определение 1. Функцию 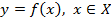
Теорема. Если функция 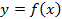
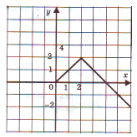
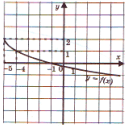
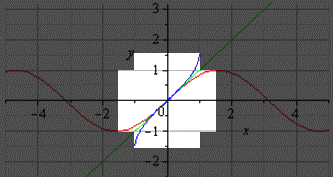
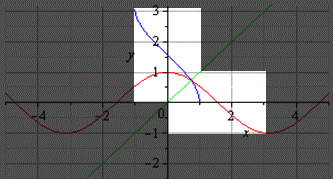
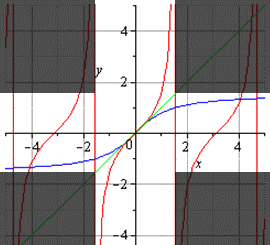
Попробуйте самостоятельно определить, какая из предложенных функций обратима?:
а)
б)
а) – функция и возрастает и убывает, значит, она немонотонна, поэтому необратима
б) – функция убывает, значит, она монотонна, поэтому обратима
в) – линейная функция, k=2, то есть функция возрастает, значит, она монотонна, поэтому обратима
г) – квадратичная функция, график – парабола, ветви вниз, то есть функция и возрастает и убывает, значит, она немонотонна, поэтому необратима
Замечание. Монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Например, мы можем взять немонотонную функцию и рассмотреть ее только на одном промежутке, где она только возрастает или только убывает, тогда условие обратимости будет выполняться. Например, функция 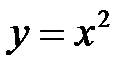
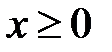
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ.
АЛГОРИТМ СОСТАВЛЕНИЯ ОБРАТНОЙ ФУНКЦИИ.
Алгоритм составления обратной функции для функции y=f(x), 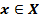
Пример 1. Показать, что для функции y=2x-5 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=2x-5 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение 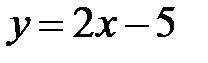
Переобозначим переменные, получим искомую обратную функцию
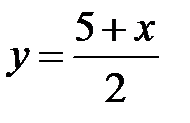
Пример 2. Показать, что для функции 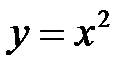
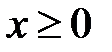
Решение. 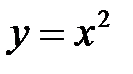
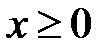
Так как по условию 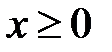
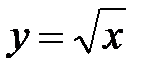
Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
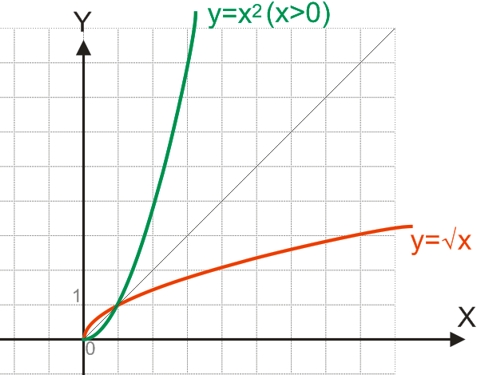
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
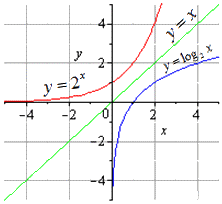
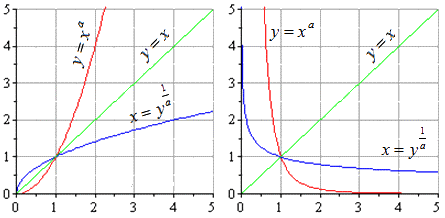
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
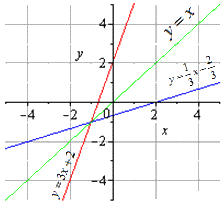
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
1 комментарий
Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?
Взаимно обратные функции, основные определения, свойства, графики
Понятие обратной функции
Для чего вообще нам нужно понятие обратных функций?
Нахождение взаимно обратных функций
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным.
Решение
Обе взаимно обратные функции можно отобразить на графике следующим образом:
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
Решение
В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
На графике обе функции будут выглядеть так:
Основные свойства взаимно обратных функций
a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = п о ф о р м у л е п р и в и д е н и я = a r c sin sin π 3 = π 3
Графики взаимно обратных функций
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
Графики для функций с a > 1 и a 1 будут выглядеть так:
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
График главной ветви косинуса и арккосинуса выглядит так:
График главной ветви арктангенса и тангенса:
График главной ветви арккотангенса и котангенса будет таким:
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Обратимые и обратные функции
Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.
Примеры обратимых функций:
Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.
Примеры обратных функций:
Однако, если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой:
Графики функций будут симметричны относительно прямой y=x:
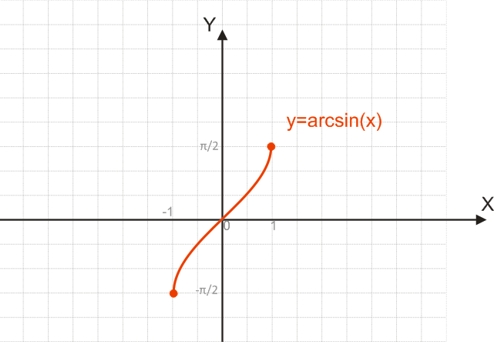
Функция y=arcsin(x)
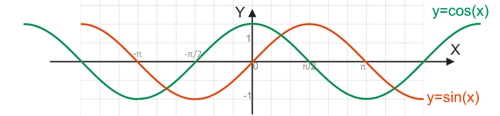
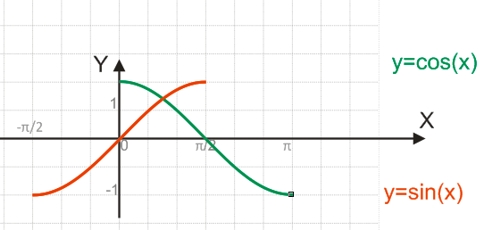
Поскольку функция y=sin(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=sin(x), необходимо взять один из полупериодов функции, обычно это отрезок [-π/2;π/2], на котором функция обратима.
График функции y=arcsin(x):
Например, чтобы найти arcsin(1), можно воспользоваться равенством 1=sin(y). Угол на отрезке [-π/2;π/2], синус которого равняется 1, будет равен 90° или π/2.
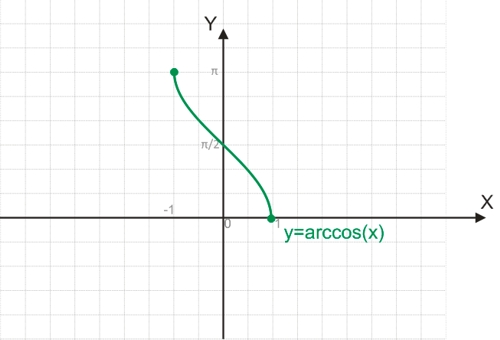
Функция y=arccos(x)
Поскольку функция y=cos(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=cos(x), необходимо взять один из полупериодов функции, обычно это отрезок [0;π], на котором функция обратима.
График функции y=arccos(x):
Например, чтобы найти arccos(1), можно воспользоваться равенством 1=cos(y). Угол на отрезке [0;π], косинус которого равняется 1, будет равен 0.
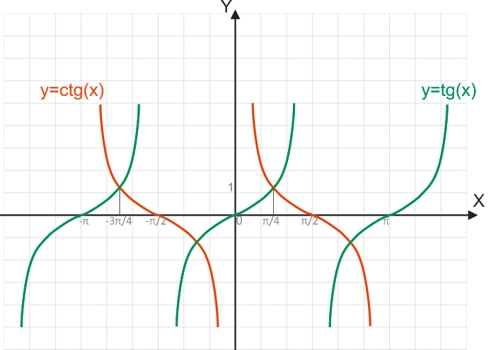
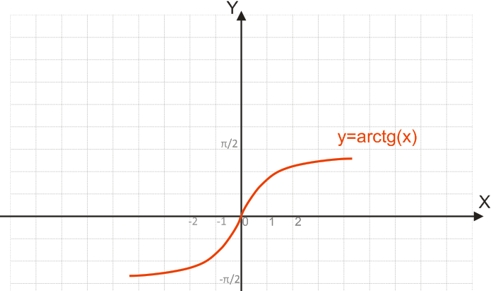
Функция y=arctg(x)
Поскольку функция y=tg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=tg(x), необходимо рассматривать тангенсоиду на отрезке [-π/2;π/2], на котором функция обратима.
График функции y=arctg(x):
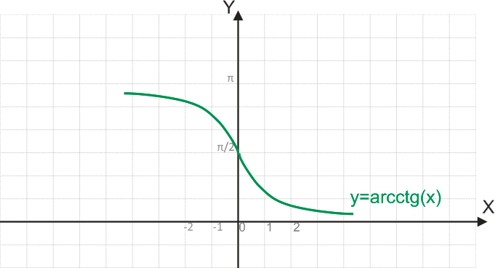
Функция y=arcctg(x)
Поскольку функция y=ctg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=ctg(x), необходимо рассматривать котангенсоиду на отрезке [0;π], на котором функция обратима.
График функции y=arcctg(x):
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Обратная функция. Урок алгебры в 10-м классе (профильный уровень)
Разделы: Математика
Воспитательная: формировать коммуникативную компетентность.
Оборудование: компьютер, проектор, экран, интерактивная доска SMART Board, раздаточный материал (самостоятельная работа) для работы в группе.
Ход урока.
1. Организационный момент.
Цель – подготовка учащихся к работе на уроке:
— настрой учащихся на работу, организация внимания;
— сообщение темы и цели урока.
2. Актуализация опорных знаний учащихся. Фронтальный опрос.
Для учащихся на интерактивной доске демонстрируется график функции. Учителем формулируется задание – рассмотреть график функции и перечислить изученные свойства функции. Учащиеся перечисляют свойства функции в соответствии со схемой исследования. Учитель справа от графика функции маркером на интерактивной доске записывает названные свойства.
По окончании исследования учитель сообщает, что сегодня на уроке они познакомятся еще с одним свойством функции – обратимостью. Для осмысленного изучения нового материала учитель предлагает ребятам познакомиться с основными вопросами, на которые учащиеся должны дать ответ по окончании урока. Вопросы записаны на обыкновенной доске и в виде раздаточного материала есть у каждого ученика (раздается до урока)
3. Объяснение нового материала.
Цель — формировать знания по новой теме в соответствии с программным материалом; изучить свойство обратимости функции и научить находить функцию, обратную данной; развивать предметную речь.
Учитель проводит изложение материала в соответствии с материалом параграфа. На интерактивной доске учитель проводит сравнение графиков двух функций, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет, тем самым подводит учащихся под понятия обратимой функции.
Затем учитель формулирует определение обратимой функции и проводит доказательство теоремы об обратимой функции, используя график монотонной функции на интерактивной доске.
Определение 1: Функцию y=f(x), x X называют обратимой, если любое свое значение она принимает только в одной точке множества X.
Учащимся предлагается сделать вывод о связи между областью определения и множеством значений обратных функций.
Для рассмотрения вопроса о способах нахождения функции обратной данной, учитель привлек двух учащихся. Ребята накануне получили задание у учителя самостоятельно разобрать аналитический и графический способы нахождения функции обратной данной. Учитель выступил в роли консультанта при подготовке учащихся к уроку.
Сообщение первого ученика.
Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Учащийся привел примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима
Затем ученик знакомит учащихся со способом нахождения обратной функции, заданной аналитически.
Затем решает два примера на нахождение функции обратной данной.
Пример 1: Показать, что для функции y=5x-3 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=5x-3 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=5x-3 относительно х; получим 
Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции.
Ответ:
Во время объяснения на интерактивной доске выполняется следующее задание:
Построить в одной системе координат график функции 
4. Первичное закрепление нового материала.
Цель – установить правильность и осознанность понимания изученного материала, выявить пробелы первичного осмысления материала, провести их коррекцию.
Учащиеся делятся на пары. Им раздаются листы с заданиями, в которых они и выполняют работу в парах. Время на выполнение работы ограничено (5-7 мин). Одна пара учащихся работает на компьютере, проектор на это время выключается и остальным ребятам не видно, как работают учащиеся на компьютере.
По окончании времени (предполагается, что с работой справилось большинство учащихся) на интерактивной доске (вновь включается проектор) показывается работа учащихся, где и выясняется в ходе проверки правильность выполнения задания в паре. При необходимости учителем проводится коррекционная, разъясняющая работа.
Самостоятельная работа в парах
5. Итог урока. По вопросам, которые были заданы перед началом лекции. Объявление оценок за урок.
Домашнее задание §10. №№ 10.6(а,в) 10.8-10.9(б) 10.12 (б)
Алгебра и начала анализа. 10 класс В 2-х частях для общеобразовательных учреждений (профильный уровень) /А.Г.Мордкович, Л.О.Денищева, Т.А.Корешкова и др.; под ред. А.Г.Мордковича, М: Мнемозина, 2007 год