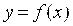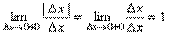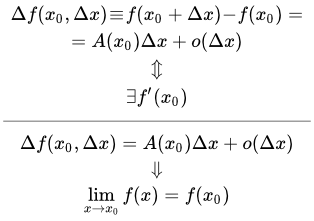Как определить что функция дифференцируема в точке
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ.



Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения 
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Доказательство. Если 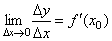
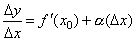
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда
Таким образом,из дифференцируемости функции следует ее непрерывность.
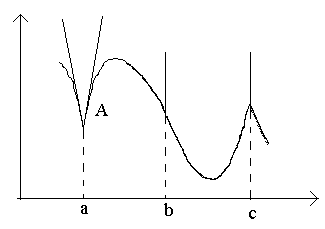
Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).
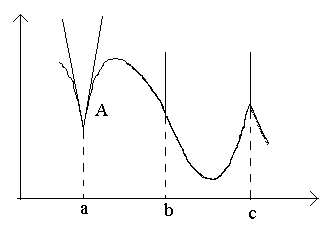
В точке a при Δx→0 отношение 

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.
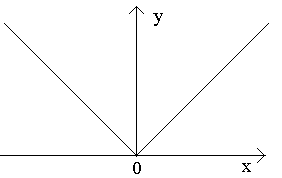
Покажем, что она не имеет производной в этой точке.
Т.о., отношение 
Дифференцируемые функции в точке – определение и свойства
Определение дифференцируемой функции
Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?
Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y ), а затем по этому направлению вычисляют производную. Поэтому в любой точке имеется бесконечное множество производных по различным направлением. Из-за этого производные не фигурируют в определении дифференцируемой функции.
Свойства дифференцируемой функции
Таким образом, в случае функции от одной переменной, дифференцируемость функции в точке эквивалентно существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.
Доказательства теорем
Связь дифференцируемости функции с существованием производной
В нашем случае это означает, что
.
Отсюда
.
Связь дифференцируемости функции с ее непрерывностью
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Как определить что функция дифференцируема в точке
При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.
Производной функции y = f ( x ) по переменной x в некоторой точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, то есть
Производная характеризует скорость изменения функции в достаточно малой окрестности заданной точки.
Приведем таблицу производных основных элементарных функций (без доказательства), которые рассматриваются нами как функции простые и явно заданные.
Следствие. В точках разрыва функция производной не имеет
Существуют такие точки, в которых функция непрерывна, но не дифференцируема. Так, функция y =| x | в точке x =0 непрерывна, но производной не имеет, так как в этой точке к графику функции можно провести бесконечное множество касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к теореме 3.9 неверно.
Среди явных функций особое место занимают обратные функции, производная которых находится с помощью следующей теоремы.
Теорема 3.10. Если строго монотонная функция y = f ( x ) дифференцируема на некотором интервале Х, причем ее производная не обращается в нуль на Х, то обратная к ней функция x = φ ( y ) также дифференцируема на этом интервале, при этом:
По определению производной можно записать:
Среди явных функций выделяют класс сложных функций.
Теорема 3.11. Чтобы продифференцировать сложную функцию необходимо сначала продифференцировать внешнюю функцию по внутренней, считая внутреннюю функцию независимой переменной, затем продифференцировать внутреннюю функцию по независимому переменному и результаты дифференцирования перемножить, то есть
Решение. Согласно формуле (3.31) и с учетом табли 
где t – параметр. Производную такой функции несложно получить:
Пример 3.9. Найти производную функции 
Решение. Согласно формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Помимо таблицы производных имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме производных этих функций:
Данная теорема может быть обобщена для произвольного конечного числа функций-слагаемых.
Решение. Согласно формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:
Теорема 3.13. Производная произведения двух дифференцируемых функций равна произведению производной первой функции-сомножителя на вторую функцию плюс произведение первой функции на производную второй функции–сомножителя, то есть
Решение. Согласно формуле (3.34) и с учетом табличных формул (3.22), (3.24) имеем:
Теорема 3.14. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть
Решение. Согласно формуле (3.35) и с учетом табличных формул (3.17), (3.29) имеем:
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.17) и (3.18) имеем:
Дифференциалом функции y = f ( x ) в точке x называется главная часть приращения этой функции, равная произведению производной функции на приращение аргумента:
Формула (3.39) применяется для вычисления приближенных значений функций.
Как определить что функция дифференцируема в точке
3.2.3. дЙЖЖЕТЕОГЙТХЕНПУФШ ЖХОЛГЙК. оЕРТЕТЩЧОПУФШ ДЙЖЖЕТЕОГЙТХЕНПК ЖХОЛГЙЙ
еУМЙ ЖХОЛГЙС ДЙЖЖЕТЕОГЙТХЕНБ Ч ЛБЦДПК ФПЮЛЕ ОЕЛПФПТПЗП ПФТЕЪЛБ [ Б ; b ] ЙМЙ ЙОФЕТЧБМБ ( Б ; b ), ФП ЗПЧПТСФ, ЮФП ПОБ ДЙЖЖЕТЕОГЙТХЕНБ ОБ ПФТЕЪЛЕ [ Б ; b ] ЙМЙ УППФЧЕФУФЧЕООП Ч ЙОФЕТЧБМЕ ( Б ; b ).
уРТБЧЕДМЙЧБ УМЕДХАЭБС ФЕПТЕНБ, ХУФБОБЧМЙЧБАЭБС УЧСЪШ НЕЦДХ ДЙЖЖЕТЕОГЙТХЕНЩНЙ Й ОЕРТЕТЩЧОЩНЙ ЖХОЛГЙСНЙ.
фБЛЙН ПВТБЪПН, ЙЪ ДЙЖЖЕТЕОГЙТХЕНПУФЙ ЖХОЛГЙЙ УМЕДХЕФ ЕЕ ОЕРТЕТЩЧОПУФШ.
еУМЙ 
ЗДЕ 

фБЛЙН ПВТБЪПН, Ч ФПЮЛБИ ТБЪТЩЧБ ЖХОЛГЙС ОЕ НПЦЕФ ЙНЕФШ РТПЙЪЧПДОПК. пВТБФОПЕ ХФЧЕТЦДЕОЙЕ ОЕЧЕТОП: УХЭЕУФЧХАФ ОЕРТЕТЩЧОЩЕ ЖХОЛГЙЙ, ЛПФПТЩЕ Ч ОЕЛПФПТЩИ ФПЮЛБИ ОЕ СЧМСАФУС ДЙЖЖЕТЕОГЙТХЕНЩНЙ (Ф.Е. ОЕ ЙНЕАФ Ч ЬФЙИ ФПЮЛБИ РТПЙЪЧПДОПК).
тБУУНПФТЙН ОБ ТЙУХОЛЕ ФПЮЛЙ Б, b, c.
ч ФПЮЛЕ b РТЙ 


жХОЛГЙС ЙНЕЕФ ВЕУЛПОЕЮОХА РТПЙЪЧПДОХА. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ЧЕТФЙЛБМШОХА ЛБУБФЕМШОХА. фЙР ФПЮЛЙ – «ФПЮЛБ РЕТЕЗЙВБ» c ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК.
ч ФПЮЛЕ c ПДОПУФПТПООЙЕ РТПЙЪЧПДОЩЕ СЧМСАФУС ВЕУЛПОЕЮОП ВПМШЫЙНЙ ЧЕМЙЮЙОБНЙ ТБЪОЩИ ЪОБЛПЧ. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ДЧЕ УМЙЧЫЙЕУС ЧЕТФЙЛБМШОЩЕ ЛБУБФЕМШОЩЕ. фЙР – «ФПЮЛБ ЧПЪЧТБФБ» У ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК – ЮБУФОЩК УМХЮБК ХЗМПЧПК ФПЮЛЙ.
тБУУНПФТЙН ЖХОЛГЙА y=|x|.
ьФБ ЖХОЛГЙС ОЕРТЕТЩЧОБ Ч ФПЮЛЕ x = 0, Ф.Л. 
рПЛБЦЕН, ЮФП ПОБ ОЕ ЙНЕЕФ РТПЙЪЧПДОПК Ч ЬФПК ФПЮЛЕ.
оП ФПЗДБ РТЙ
б РТЙ 
ф.П., ПФОПЫЕОЙЕ 

4.02. Дифференцируемость функции в точке и на промежутке
Производная функции, согласно ее математического определения (1.5) и (1.6) – это некий предел. Но, как и всякий предел, он может оказаться:
А) конечным; б) бесконечным; в) вообще не существовать.
Если для данного X имеет место вариант (а), то есть если при заданном X производная 
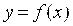
Функция, дифференцируемая в Каждой точке X некоторого промежутка оси Ох (например, интервала (A; B) или отрезка [A; B]) называется Дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее Дифференцированием (продифференцировать функцию – это значит найти ее производную).

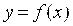
1) Существование касательной к графику функции в его точке с абсциссой X.
2) Невертикальность этой касательной (ибо 
Например, функция 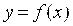
Действительно, точке X1 соответствует на графике функции точка M1 с вертикальной касательной. Точке X2 (точке максимума функции) соответствует остроконечная вершина M2, касательная в которой не существует. Точке X3 соответствует точка M3 – точка излома графика функции, в которой тоже касательная не существует.
Во всех же остальных точках M графика функции касательную к графику провести можно, и она невертикальна. Значит, для всех остальных X, отличных от (X1; X2; X3), существует производная функции. То есть во всех остальных точках X функция