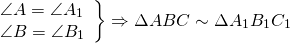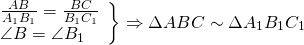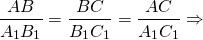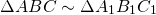Как доказать что треугольники подобны
Как доказать что треугольники подобны
Признака подобия треугольников
Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F
F’`. Напомним, что запись подобия треугольников `Delta ABC
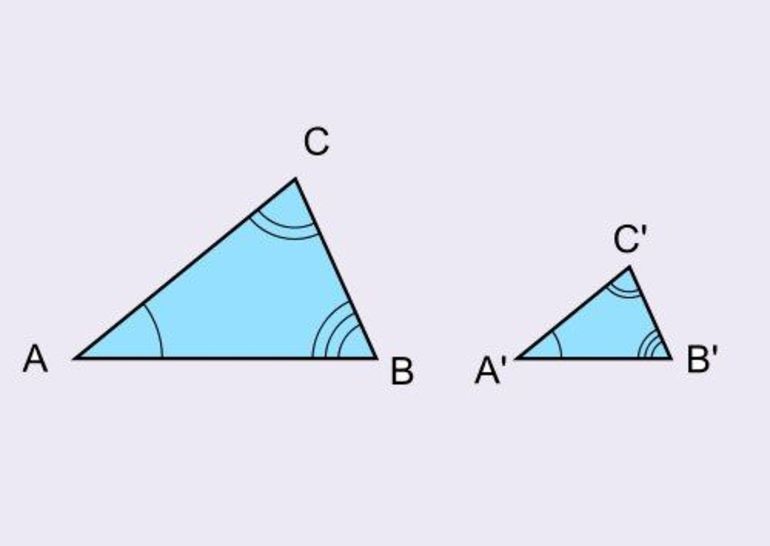
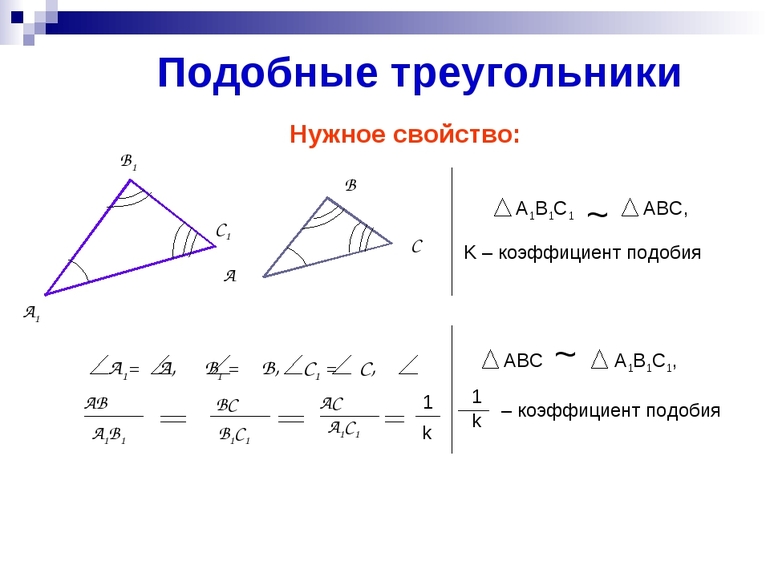
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC
Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,
`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.
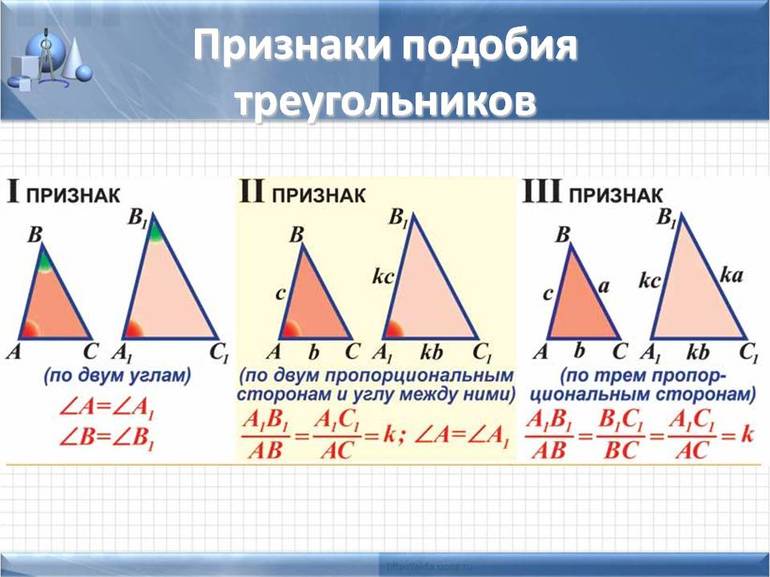
Два треугольника подобны, если:
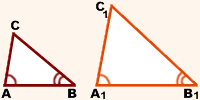
1. два угла одного соответственно равны двум углам другого;
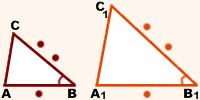
2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
3. три стороны одного треугольника пропорциональны трём сторонам другого.
В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.
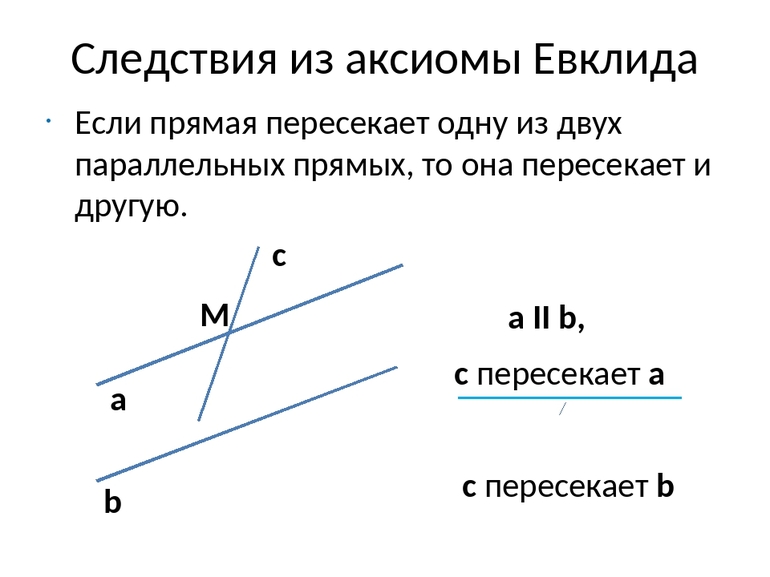
Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.
Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.
И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.
Delta COB` по двум углам (рис. 10б):
`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.
3. Учитывая, что `BD = BO + OD` находим отношение
`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.
Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.
Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.
Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.
Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.
Попытайтесь доказать это самостоятельно.
Прямоугольные треугольники подобны, если:
1. они имеют по равному острому углу;
2. катеты одного треугольника пропорциональны катетам другого;
3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.
Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.
Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.
СВОЙСТВА ВЫСОТ И БИССЕКТРИС
Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C
Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).
Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).
В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.
Таким образом, `Delta A_1 B_1 C
$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos C =b \cos C;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos C =a \cos C,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC,$$
коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.
$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos\varphi =b |\cos C|;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos\varphi =b |\cos C|,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC$$
с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.
В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).
Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).
Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).
По первой лемме о высотах `Delta A_1 B_1 C
Delta ABC`, `/_ A_1 B_1 C = /_ B`.
Аналогично `Delta AB_1C_1
Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.
Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.
Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.
Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.
Установим ещё одно свойство биссектрисы угла треугольника.
Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.
По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.
Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16
Признаки подобия треугольников
Признаки подобия треугольников позволяют доказать, что треугольники являются подобными, на основании 2-3 равенств (вместо 6 по определению).
В школьном курсе геометрии, как правило, изучают три признака подобия произвольных треугольников.
( подобие треугольников по двум углам)
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
( подобие треугольников по двум сторонам и углу между ними)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
( подобие треугольников по трём сторонам)
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Есть еще 4-й признак подобия треугольников —
( подобие треугольников по двум сторонам и наибольшему углу)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а наибольший угол одного равен наибольшему углу другого, то такие треугольники подобны.
Доказав, что треугольники подобны, можно использовать свойства подобных треугольников.
Для доказательства подобия прямоугольных треугольников используют другие признаки. Их мы запишем в следующий раз.
Подобие правильных и подобие равнобедренных треугольников рассмотрим позже.
Признаки подобия треугольников широко используются при решении задач как в курсе планиметрии, так и в курсе стереометрии. Например, на основании подобия прямоугольных треугольников доказывается свойство биссектрисы треугольника.
Общие сведения
Специалисты рекомендуют начинать любое обучение с азов. Следует применять принцип, который называется «от простого к сложному». В плоскостной геометрии (Евклида) существует два понятия: аксиомы и теоремы. К первым относятся утверждения, не требующие доказательства. Они являются базовыми элементами науки и позволяют доказывать другие гипотезы или утверждения.
Кроме того, на основании доказанных гипотез можно производить операции по доказательству более сложных теорем. Иными словами, геометрия состоит из базисных элементов — аксиом, при использовании которых можно преобразовывать утверждения в неоспоримые факты, а также при комбинациях появляется возможность доказательства более сложных (составных) элементов. Примером последнего случая является гипотеза Пифагора для прямоугольного треугольника. Чтобы ее доказать, нужно знать аксиомы геометрии, а также теорему об отношении площадей подобных треугольников (S/S’). Далее необходимо разобрать основные объекты геометрии.
Объекты геометрии
Простейшим объектом геометрии является точка. С помощью нее строятся простые фигуры, благодаря которым образуются более сложные формы. К элементарным компонентам можно отнести следующие: прямая, отрезок, луч. Первая состоит из множества точек, соединенных между собой в одной плоскости и находящихся в поперечном сечении, диаметр которого эквивалентен диаметру точек. При соединении простейших объектов получается бесконечная линия без перегибов.
Лучом называется часть прямой, имеющая начальную точку, но у которой нет конечной границы. Еще существует один элемент, у которого присутствуют обе границы (левая и правая). Он называется отрезком. Следует отметить, что луч и отрезок могут лежать на одной прямой, а также последний может являться частью первого.
При комбинации двух лучей, исходящих из одной точки получается плоский угол. Он измеряется в градусах или радианах. Следует отметить, что в геометрии существует понятие «нулевого» угла. Это возможно, когда лучи совпадают. При комбинации трех углов можно получить треугольник. Существует также другое определение этой фигуры: треугольником (Δ) называется фигура, состоящая из трех точек, одна из которых не лежит на одной прямой с остальными.
Треугольники бывают разносторонними, равнобедренными и равносторонними. Кроме того, в зависимости от градусной меры, они делятся на такие классы: остроугольные, тупоугольные и прямоугольные. Необходимо также отметить, что сумма углов этой геометрической фигуры эквивалентна 180 градусам.
Нужно обратить внимание на такие термины: высоту, медиану и биссектрису. Первой называется перпендикуляр, проведенный из вершины к противоположной стороне. Медиана — отрезок, проведенный из противоположной вершины к середине стороны. Биссектрисой угла является луч или отрезок, который делит его на два равнозначных по величине. В равнобедренном и равностороннем Δ эти элементы совпадают.
Основные аксиомы Евклида
Аксиомой называется утверждение, не требующее доказательств и воспринимаемое в виде факта. Существуют следующие утверждения, которые можно применять при решении задач:
Следует обратить внимание на последнюю аксиому. Она позволяет строить любые фигуры на плоскости и в пространстве. Математики очень часто применяют такой прием при решении задач и доказательстве некоторых тождеств при помощи создания дополнительных элементов на чертеже.
Например, в некотором упражнении по нахождению отдельных параметров треугольника в условии содержится очень мало данных. Последний можно вписать в окружность или дополнить до квадрата или прямоугольника. Далее следует разобраться в признаках подобия треугольников.
Подобие двух треугольников
Треугольники являются подобными, когда углы одного эквивалентны всем градусным мерам углов другого, а стороны одного равны сторонам другого, с учетом коэффициента гомотетии. Последний называют еще коэффициентом подобия. Он равен отношению сторон подобных треугольников. Например, дано два подобных Δ ABC и A’B’C’ (больший). Коэффициент подобия треугольников обозначается литерой «k». Он больше 0 и вычисляется по такой формуле: k = A’B’ / AB = B’C’ / BC = A’C’ / AC. Подобие фигур обозначается таким образом: ΔABC ∼ ΔA’B’C’.
Не во всех случаях бывают известны углы и стороны фигур. Для этого были сформулированы три признака (условия или критерия), по которым можно определить подобие.
Первое условие
Формулировка первого признака подобия треугольников гласит, что равенство двух углов между собой соответствует подобию двух фигур. Подробнее исходные данные записываются в таком виде: ΔABC ∼ ΔA’B’C’, когда ∠ВАС = ∠B’A’C’ и ∠ABC = ∠A’B’C’. Доказать утверждение довольно просто. Для этого следует рассчитать третий угол у треугольников исходя из того, что сумма трех углов составляет 180 градусов.
Далее необходимо наложить один Δ на другой, чтобы ∠ВАС совпал с ∠B’A’C’. Используя теорему Фалеса для сторон угла, которые делят на отрезки AC / A’C’ = BC / B’C’ вершины малого Δ на пропорциональные части. Аналогично доказывается пропорциональность для двух других сторон. Однако для этого следует наложить уже треугольники таким образом, чтобы совпали другие углы. Такие же действия проделать и для третьего угла. На основании определения о подобии треугольников утверждение доказано. Из доказательства математики получили некоторые следствия, которые будут очень полезны при решении задач:
Равенство AC / A’C’ = BC / B’C’ эквивалентно коэффициенту подобия. Этот факт можно использовать при решении задач и доказательства других геометрических утверждений или тождеств.
Второй критерий
Математики выделяют еще один признак подобия треугольников по двум пропорциональным сторонам и углу между ними. Для доказательства следует рассмотреть ΔABC и ΔA’B’C’ со сторонами, связанными таким тождеством: AB / A’B’ = AC / A’C’. Кроме того, углы между ними равны: ∠ВАС = ∠B’A’C’. Далее нужно достроить ΔABC до четырехугольника ABCС». Вершина С» должна располагаться в зеркальном отображении относительно стороны AB. Полученный ΔABC» ∼ ΔA’B’C’ по I признаку, поскольку у них два угла равны. Следовательно, тождество можно править таким образом: AB / A’B’ = AC» / A’C’.
По условию должно выполняться условие AB / A’B’ = AC / A’C’. Тогда AC = AC». На основании этого факта можно сделать вывод о равенстве ΔABC и ΔABC». Следовательно, теорема доказана, поскольку эти треугольники (ΔABC» и ΔA’B’C’) подобны по I признаку.
Третий признак
Третий признак подобия двух треугольников формулируется таким образом: два треугольника являются подобными, когда стороны одного пропорциональны сторонам другой фигуры. Для доказательства необходимо рассмотреть ΔABC и ΔA’B’C’ со сторонами: AB / A’B’ = AC / A’C’ = BC / B’C’.
Математики рекомендуют отметить некоторую точку C» относительно стороны AB. Она не должна лежать на последней. Кроме того, расстояния от C и C» до стороны AB должны быть эквивалентны. Иными словами, следует построить ΔABС», который является «зеркальным» отображением ΔABC относительно его стороны AB. Если AB / A’B’ = AC» / A’C’, то ΔABC» ∼ ΔA’B’C’ по I признаку.
Следующий шаг — доказательство равенства ΔABC и ΔABC». Они равны по двум сторонам AC = AC» и BC = BC». Следовательно, ΔABC ∼ ΔA’B’C’ подобные.
Теорема об отношении площадей
Для решения задач специалисты рекомендуют применять еще теорему об отношении площадей. Обязательным условием ее использования являются ΔABC ∼ ΔA’B’C’ с коэффициентом подобия «k». Ее формулировка имеет такой вид: величина отношения площадей двух подобных треугольников прямо пропорциональна квадрату гомотетии.
Некоторые свойства и следствия
Математики также считают, что используя некоторые свойства и следствия из теорем, можно расширить возможности по решению задач. Свойства подобных треугольников можно применять и к другим плоским или объемным фигурам. Следствия классифицируются на несколько типов:
Пример решения
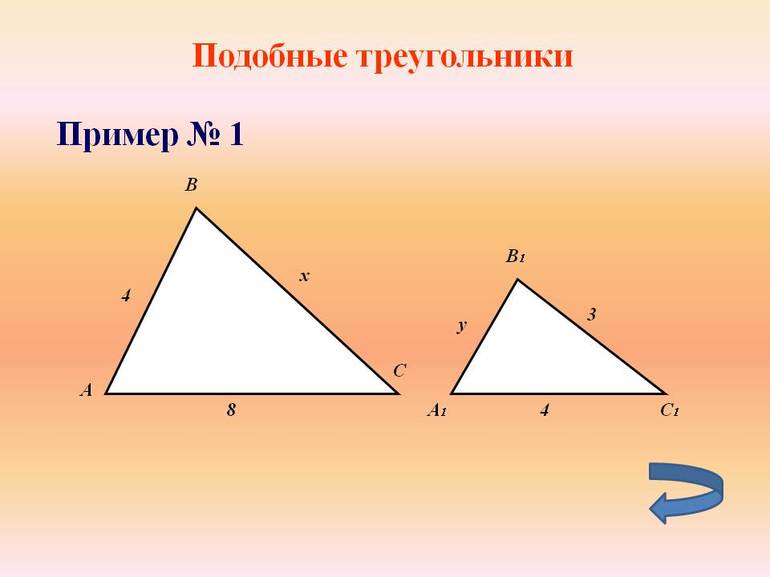
Существуют множество типов задач, однако наиболее часто попадаются такие, в которых необходимо доказать, что фигуры являются подобными. Стороны ΔABC равны таким значениям: 10, 12 и 25. Кроме того, существует еще ΔA’B’C’ со сторонами 5, 6 и 10. Фигуры не имеют точек пересечения. Необходимо доказать их подобие.
Для решения рисунок чертить необязательно, поскольку для доказательства необходимо применение не геометрического метода, а алгебраического. Следует ввести обозначения для ΔABC: AB = 10, BC = 12 и AC = 25. Аналогичную процедуру необходимо сделать для ΔA’B’C’: сторона A’B’ равна числу 5, B’C’ = 6 и A’C’ = 10.
Далее нужно вычислить коэффициент k для каждой из сторон: k1 = AB / A’B’ = 10 / 5 = 2, k2 = BC / B’C’ = 12 / 6 = 2 и k3 = AC / A’C’ = 25 / 10 = 2,5. Из соотношений следует, что фигуры не являются подобными, поскольку не выполняется такое равенство: k = k1 = k2 = k3. Для наглядности можно построить также таблицу со значениями коэффициентов.
Таким образом, для решения задач по нахождению параметров подобных треугольников необходимо знать признаки подобия, а также некоторые свойства, которые рекомендуют использовать специалисты-математики.
Подобие треугольников (ЕГЭ — 2022)
Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.
А вот что такое подобные треугольники? Вроде как «похожие», но как это понимать? И для чего это понимать?
Ну например для решения задание ЕГЭ №16, где подобие треугольников используется для доказательств. Кстати, полностью 16-ю задачу решают менее 1% выпускников!
Читай эту статью, смотри вебинар по 16 задаче и все поймешь!
Подобие треугольников — коротко о главном
Подобные треугольники – это треугольники, у которых все углы равны и все стороны строго пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия \( \displaystyle k\).
\( \angle A = \angle
Отношение периметров подобных треугольников равно коэффициенту подобия: \( \displaystyle \frac<<
_ _<<_<1>><_<1>>< Отношение площадей подобных треугольников равно квадрату коэффициента подобия: \( \displaystyle \frac<< Признаки подобия треугольников: По двум углам: По одному углу и отношению заключающих его сторон: По отношению трех сторон: Мы разобрали подробно все, что касается треугольников в общем. Кроме того мы рассмотрели отдельные темы: Но что такое подобные треугольники? Вот, например, такой и такой: Похожи эти треугольники? Ты скажешь, конечно же нет! А вот такой и такой? Посмотри внимательно, тоже похожи. А теперь строго математически! Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны. То есть все углы равны и все стороны одного треугольника в \( \displaystyle 5\), или, в \( \displaystyle 7\), или в \( \displaystyle 8,21\) (или и т.д.) больше сторон другого треугольника. Записываются слова «треугольник \( \displaystyle ABC\) подобен треугольнику \( \displaystyle <_<1>><_<1>>< То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы \( \displaystyle k\). \(\angle A = \angle Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон. Помнишь еще, что «\( \displaystyle \sim<\ >\)» обозначает слова «подобен»? Осознай удобство! Вместо того, чтобы проверять 6 утверждений – 3 равных угла и 3 пропорциональных стороны – ДОСТАТОЧНО РАВЕНСТВА ВСЕГО ДВУХ УГЛОВ! И это вообще-то самых удобный и часто используемый признак. Но есть и еще два. Смотри. Признаки нам рассказали о том, как обнаружить подобные треугольники, а теперь, как же воспользоваться найденным? Ну вот, что же хорошего? А то, что тогда… Все элементы одного треугольника ровно в \( \displaystyle 2\) (или сколько у тебя выйдет раз) больше, чем элементы другого треугольника. Не только стороны, но и высоты, биссектрисы, медианы, радиусы вписанной и описанной окружности и т.д. Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы. В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение. Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем. Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).__<<_<1>><_<1>><Подобные треугольники — подробнее
Признак подобия треугольников «по двум углам»
Признак подобия треугольников «две пропорциональные стороны и угол между ними»
Признак подобия треугольников «три пропорциональные стороны»
Самый главный «секрет» подобия треугольников
Читать далее…
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 16. Подобие треугольников. Задачи на доказательство