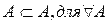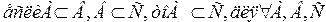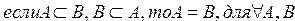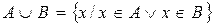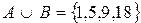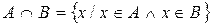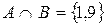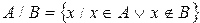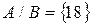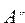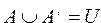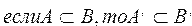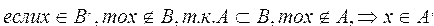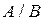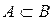Как доказать что одно множество является подмножеством другого
Множества
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
Подмножество — это множество, все элементы которого, являются частью другого множества.
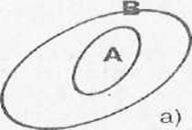
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :
Рассмотрим два множества:
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
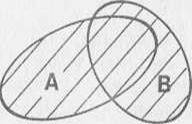
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
При объединении равных множеств объединение будет равно любому из данных множеств:
Множество и его элементы. Подмножества
Понятие множества
Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».
Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».
Приведём примеры множеств:
Множество людей в салоне самолёта
Множество деревьев в парке
Множество планет Солнечной системы
Множество электронов в атоме
Множество натуральных чисел
Множество «синих-синих презелёных красных шаров»
Конечное, бесконечное и пустое множества
Людей в салоне самолёта легко посчитать, это множество конечно.
С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.
Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.
Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.
Помидоры на грядке
Числа (натуральные, рациональные, действительные и т.д.)
Количество рациональных чисел на отрезке [0;1]
Полосатые летающие слоны
Все точки пересечения двух параллельных прямых на плоскости
Способы задания множеств
1) Перечисление – в списке задаются все элементы множества.
Множество всех континентов Земли:
Множество букв слова «математика»:
Множество натуральных чисел меньших 5:
2) Характеристическое свойство – указывается особенность элементов множества.
D =
3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)
Подмножества
Говорят, что B содержит A, или B покрывает A.
Пустое множество является подмножеством любого множества.
Множество людей является подмножеством приматов, живущих на Земле.
Множество квадратов является подмножеством прямоугольников.
Множество всех подмножеств данного множества A называют булеаном или степенью множества A.
Примеры
Пример 1. Запишите данное множество с помощью перечисления элементов:
Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:
Задано множество целых чисел, модуль которых не больше 3. Перечисляем:
Задано множество рациональных чисел, являющихся корнями уравнения
(x-1)(2x+5) = 0. Перечисляем:
Пример 2. Запишите данное множество с помощью характеристического свойства:
а) Множество всех натуральных чисел меньше 10
б) Множество всех действительных чисел, кроме 0
в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1
Пример 3. Изобразите на графике в координатной плоскости данное множество:
Задано конечное множество точек, которое можно представить перечислением:
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:
Множество и его элементы. подмножество. пустое множество.
Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.
Запись 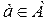
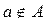
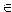
Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.
Например: <2, 4, 6>= <4, 2, 6>– равные множества.
Определение 2. Множество называется непустым, если содержит хотя бы один элемент.
Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
В этом случае пишут 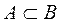
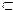
Например: <2, 4,>
Рассмотрим свойства отношения включения.
рефлексивно, т.е любое множество является подмножеством самому себе.
транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.
антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.
Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.

Пустое множество является подмножеством любого множества.
Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).
В дальнейшем будем пользоваться следующим утверждением:
Утверждение 1. Число всех подмножеств конечного множества равно 2n.
Пример. Выделим все подмножества множества А =<2, 4, 6>.
Р(А)=<2, 4, 6>, <2, 4>, <4, 6>, <2, 6>, <2>, <4 >, <6>, 
Операции над множествами
Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.
Для обозначения объединения множеств используют знак 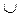
Пример. 

Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.
Для обозначения пересечения множеств используют знак 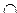
Пример. 

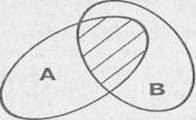
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.
Для обозначения разности множеств используют знак /.
Пример. 

Перечислим основные свойства операций над множествами:
1) 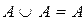
2) 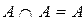
3) 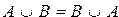
4) 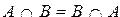
5) 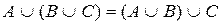
6) 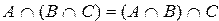
7) 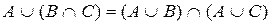
8) 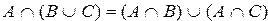
Универсальное множество. Дополнение множества.
Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.
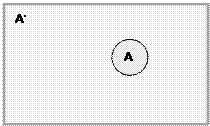
Определение 6. Множество U/А называется дополнением множества А и обозначается 

Дополнение U/ 

Справедливы следующие формулы:
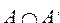
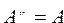
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.
Пусть множество А является подмножеством множества В, 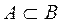
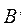

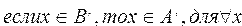
Действительно, если х принадлежит множеству 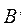

Теорема. Имеют место следующие тождества
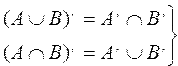
Приведем краткое доказательство первого утверждения.
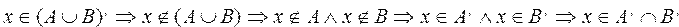
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.
Объединение множеств Пересечение множеств
Разность множеств Подмножество
Универсальное множество Дополнение
 |  |
Понятие множества. Элементы множества. Пустое множество. Принадлежность элементов.
§1. Множества и операции над ними
Объяснение и обоснование
В курсах алгебры и алгебры и начал математического анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество М состоит из чисел 1; 2; 3, то его обозначают так: М = <1; 2; 3>. Тот факт, что число 2 входит в это множество (является элементом данного множества М), записывается с помощью специального значка ∈ следующим образом: 2 ∈ М; а то, что число 5 не входит в это множество (не является элементом данного множества), записывается так: 5 ∉ М.
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например: множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом ∅, множество всех натуральных чисел — буквой N, множество всех целых чисел — буквой Z, множество всех рациональных чисел — буквой Q, а множество всех действительных чисел — буквой R.
Множества бывают конечными и бесконечными в зависимости от того, какое количество элементов они содержат. Так, множества А = <7>и M = <1; 2; 3>— конечные, потому что содержат конечное число элементов, а множества N, Z, Q, R — бесконечные.
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило (характеристическое свойство), которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, А = <–1; 0; 1>(множество задано перечислением элементов), B — множество всех четных целых чисел (множество задано характеристическим свойством всех элементов множества). Последнее множество иногда записывают так: B = или так: B =
В общем виде запись множества с помощью характеристического свойства можно обозначить так: A =
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, <1; 2; 2>= <1; 2>, поскольку каждый элемент первого множества (1 или 2) является элементом второго множества и, наоборот, каждый элемент второго множества (1 или 2) является элементом первого. Поэтому, записывая множество, чаще всего каждый его элемент записывают только один раз.
Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.
Это записывают следующим образом: A ⊂ B.
Например, <1; 2>⊂ <0; 1; 2; 3>, N ⊂ Z (поскольку любое натуральное число — целое), Z ⊂ Q (поскольку любое целое число — рациональное), Q ⊂ R (поскольку любое рациональное число — действительное).
Полагают, что всегда ∅ ⊆ A, то есть пустое множество является подмножеством любого множества.
Иногда вместо записи A ⊂ B используется также запись A ⊆ B.
Сопоставим определение равенства множеств с определением подмножества. Если множества А и В равны, то: 1) каждый элемент множества А является элементом множества В, следовательно, А — подмножество В (A ⊆ B); 2) каждый элемент множества В является элементом множества А, следовательно, В — подмножество А (B ⊆ A). Таким образом,
два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера–Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами N, Z, Q, R.