Как доказать что это составное число
Лекция 8. 22.04.20.ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
Лекция 8. Простые и составные числа. Их свойства
Определение. Натуральное число, большее единицы, называется простым, если оно делится только на себя и на 1 (т. е. имеет ровно два разных делителя). Натуральное число называется составным, если оно имеет более 2 разных делителей.
Например, числа 2, 3, 5, 7, 11 – простые, а число 18 – составное (1, 2, 3, 6, 9, 18 – его делители). Число 1 имеет только один делитель и не является ни простым, ни составным.
Таким образом, множество целых неотрицательных чисел N0 можно разделить на четыре непересекающихся подмножества:
1) <0>– множество, состоящее из одного элемента, числа 0:;
2) <1>– множество, состоящее из одного элемента, числа 1;
1) Если простое число p делится на натуральное число q ≠ 1, то q совпадает с числом p (q = p).
Доказательство. Действительно, если бы число p делилось на q и не совпадало с числом q, то оно имело бы три делителя: 1, p, q, что противоречит определению простого числа. Поэтому p = q.
2) Если p и q – разные простые числа, то p не делится на q.
Доказательство. Поскольку p – простое число, то оно делится только на 1 и p. По условию p ≠ q и q – простое число, значит, q ≠ 1. Отсюда следует, что p не делится на q.
3) Всякое натуральное число a>1 имеет хотя бы один простой делитель, причем этот делитель наименьший.
Доказательство. Если число а – простое, то таким делителем числа а является само это число.
Последнее неравенство противоречит условию, что d – наименьший делитель числа а. Значит, допущение о том, что число d – составное, ошибочно.
Таким образом, наименьший делитель натурального числа а – всегда простое число.
Доказательство. Пусть число а – составное и d – его наименьший простой делитель (он существует на основании свойства 3).
Число 381 – составное, поскольку делится на 3 по признаку делимости.
Решето Эратосфена
Эратосфен – древний греческий ученый математик и астроном, который жил в III в. до н. э. Считают, что он первый составил таблицу простых чисел. В древности греки писали палочками на восковых досках. Записав некоторую последовательность натуральных чисел, Эратосфен прокалывал дырку, где стояли составные числа. Составные числа как бы «просеивались», а оставались только простые. Дощечка выглядела подобно решету. Отсюда, возможно, и название метода Эратосфена отсеивать составные числа.
Решение. Запишем последовательность натуральных чисел от 2 до 40.
Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Составное число – это натуральное число, имеющее более двух положительных делителей.
Натуральные числа, которые не являются простыми, называют составными.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Рассмотрим теорему, которая объясняет последнее утверждение.
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Простых чисел бесконечно много.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.
Решето Эратосфена
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Перейдем к формулировке теоремы.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Доказать что число 898989898989898989 является составным.
Ответ: 11723 является составным числом.
Как доказать что это составное число
Составные числа
Число так называемых простых чисел, т. е. целых чисел, больших единицы, не делящихся без остатка ни на какие другие целые числа, кроме единицы и самих себя, бесконечно велико.
Для удобства будем пользоваться условным символом n!, который обозначает произведение всех чисел от 1 до n включительно. Например 5! = 1 × 2 × 3 × 4 × 5. Мы сейчас докажем, что ряд
включительно состоит из n последовательных составных чисел.
состоит из двух слагаемых, каждое из которых кратно 3. Значит, и это число составное.
делится без остатка на 4, так как состоит из слагаемых, кратных 4.
Подобным же образом устанавливаем, что следующее число
кратно 5 и т. д. Иначе говоря, каждое число нашего ряда содержит множитель, отличный от единицы и его самого; оно является, следовательно, составным.
Если вы желаете написать, например, пять последовательных составных чисел, вам достаточно в приведенный выше ряд подставить вместо n число 5. Вы получите ряд
Или еще меньшие числа:
Попробуем теперь решить задачу:
Написать десять последовательных составных чисел.
На основании ранее сказанного устанавливаем, что в качестве первого из искомых десяти чисел можно взять
Искомой серией чисел, следовательно, может служить такая!
Однако существуют серии из десяти гораздо меньших последовательных составных чисел. Так, можно указать на серию даже не из десяти, а из тринадцати составных последовательных чисел уже во второй сотне:
Простые числа. Составные числа
Определение 1. Простое число − это натуральное число больше единицы, которое делится только на себя и на 1.
Другими словами число является простым, если имеет только два различных натуральных делителя.
Определение 2. Любое натуральное число, которое кроме самого себя и единицы имеет и других делителей, называется составным числом.
Другими словами натуральные числа, не являющиеся простыми числами, называются составными. Из определения 1 следует, что составное число имеет больше двух натуральных делителей. Число 1 не является ни простым, ни составным т.к. имеет только один делитель 1 и, кроме этого многие теоремы относительно простых чисел не имеют места для единицы.
Из определений 1 и 2 следует, что каждое целое положительное число больше 1 является либо простым, либо составным числом.
Ниже представлена программа для отображения простых чисел до 5000. Заполните ячейки, нажмите на кнопку «Создать» и подождите несколько секунд.
Таблица простых чисел
Теорема 1. Любое составное число всегда может быть представлено и притом единственным способом в виде произведения конечного числа простых чисел.
Если k1 число простое, то k уже представлен в виде произведения простых чисел, в противном случае существует такое простое число p2, что
Если k2 число составное, то мы продолжаем процедуру до тех пор, пока k не будет представлено в виде произведения простых чисел:
Первая часть теоремы доказана. Покажем, далее, что разложение составного числа на простые множители единственно (естественно, порядок множителей в произведении может быть другим).
Допустим существует два разложения числа k:
Так как k=p1p2p3. делится на простое число q1, то по крайней мере один из множителей, например p1 делится на q1. Но p1 простое число и делится только на 1 и на себя. Следовательно p1=q1 (т.к. q1≠1)
Таким образом убеждаемся, что всякое простое число входящее множителем в первое разложение один или несколько раз, входит и во второе разложение минимум столько же раз и наоборот, всякое простое число, которое входит множителем во второе разложение один или несколько раз входит и в первое разложение минимум столько же раз. Следовательно любое простое число входит множителем в оба разложения одинаковое число раз и, таким образом, эти два разложения одинаковы.■
Разложение составного числа k можно записать в следующем виде
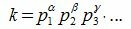 | (3) |
Разложение (3) называется каноническим разложением числа.
Теорема 2. Количество простых чисел бесконечно много.
Доказательство. Предположим, что существует конечное число простых чисел, и пусть наибольшее простое число равно p. Рассмотрим все числа больше p. По предположению утверждения эти числа должны быть составными и должны делится по крайней мере на один из простых чисел. Выберем число, являющиеся произведением всех этих простых чисел плюс 1:
Число z больше p так как 2p уже больше p. p не делится ни на одно из этих простых чисел, т.к. при делении на каждое из них дает остаток 1. Таким образом мы приходим к противоречию. Следовательно существует бесчисленное множество простых чисел.
Данная теорема является частным случаем более общей теоремы:
Теорема 3. Пусть задана арифметическая прогрессия
где d разность арифметической прогрессии, m первый член, и пусть d и m взаимно простые числа. Тогда арифметическая прогрессия (5) содержит бесконечное множество простых чисел.
Нетрудно заметить, что при m=1 и d=1 мы получим теорему 2.
Число и сумма всех делителей числа
Теорема 1 дает возможность определить, делится число m на n, если эти числа разложены на простые множители.
Если m делится на n, то n является кратным m:
Тогда любое простое число, входящее в n, должно входить и в m, поэтому в n не могут входить другие простые множители, которые не входят в m и притом эти простые множители в n входят не более число раз, чем в m.
Справедливо и обратное. Если каждый простой множитель числа n входит по крайней мере столько же раз в число m, то m делится на n.
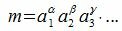 |
Тогда все делители n числа m можно представить формулой
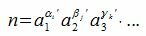 | (6) |
Каждая из чисел n вычисленная формулой (6) является делителем числа m.
Очевидно, при разных значениях i, j, k имеем разные делители числа m. Тогда число всех делителей m равно:
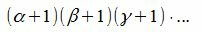 |
Мы доказали следующую теорему:
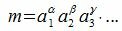 |
каноническое разложение числа m. Тогда число делителей числа m равно:
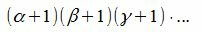 |
Составим все произведения вида 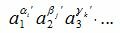
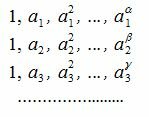 |
Тогда для произведения вида 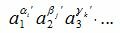
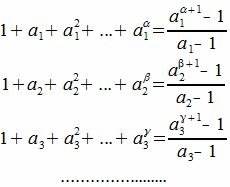 |
Заметим, что правая часть каждой строки является суммой членов геометрической прогрессии.
Следовательно сумма всех делителей числа m равна
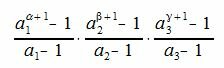 | (7) |
Мы доказали следующую теорему:
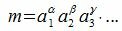 |
каноническое разложение числа m. Тогда сумма всех делителей числа m равна выражению (7).
Простые и составные числа
§ 5. Простые и составные числа.
Ранее рассматривались некоторые связи, отношения и операции между числами. Рассмотрим структуру самих чисел.
Определение 1. Натуральное число 1 называется простым, если оно не имеет делителей, отличных от 1 и a , т. е. оно имеет только два различных делителя 1 и a.
Натуральное число a называют составным, если оно имеет делители, отличные от 1 и a, т. е. имеет более двух различных делителей.
Число 1 не является ни простым, ни составным.
Примеры: простые – 2, 3, 5, 7, 11, 13, 17, 19, …
составные – 4, 6, 8, 9, 10, …
Свойства простых чисел.
10. Если произведение нескольких натуральных чисел делится на простое число p, то по крайней мере один из сомножителей делится на p.
Доказательство.
20. Наименьший отличный от единицы делитель натурального числа 
Доказательство. Пусть 






30. Наименьший отличный от единицы делитель составного числа не больше, чем 
Доказательство. Пусть 
Причем, 


Следствие. 1). Всякое составное число a имеет по крайней мере один простой делитель не более 
2). Если положительное число 















