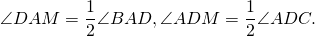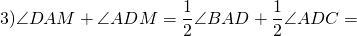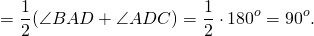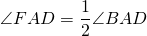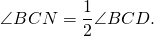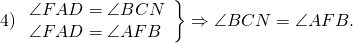Как доказать что биссектрисы противоположных углов параллелограмма параллельны
Биссектрисы углов параллелограмма
Какими свойствами обладают биссектрисы углов параллелограмма? Для биссектрис углов, прилежащих к одной стороне параллелограмма, и для биссектрис противолежащих углов эти свойства разные.
Свойство биссектрис углов параллелограмма, прилежащих к одной стороне.
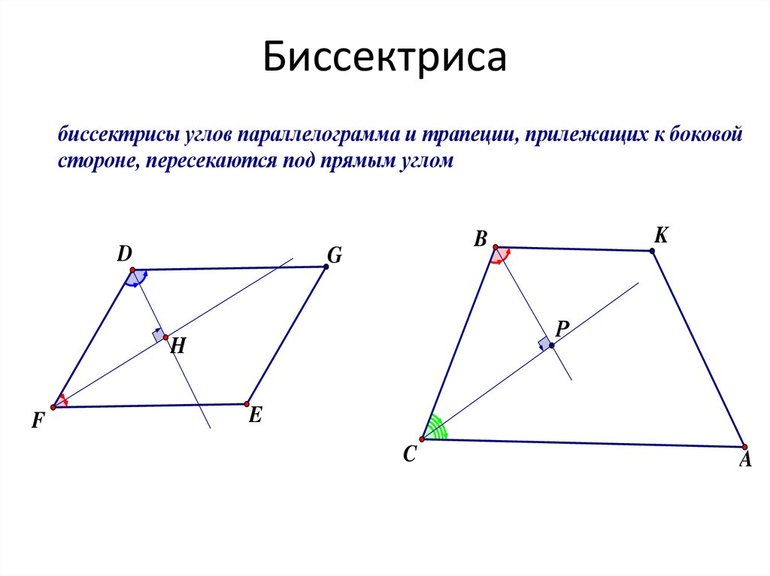
Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны.
Дано: ABCD — параллелограмм,
AF биссектриса ∠BAD,
DK- биссектриса ∠ADC,
1) ∠BAD+∠ADC=180º (как внутренние односторонние углы при AB ∥ CD и секущей AD).
2) Так как биссектриса угла делит его пополам, то
4) Рассмотрим треугольник ADM. Так как сумма углов треугольника равна 180º, то
90º+∠AMD=180º, откуда ∠AMD=180º- 90º=90º,
то есть биссектрисы углов параллелограмма, прилежащие к стороне AD, перпендикулярны.
Что и требовалось доказать.
В следующий раз рассмотрим свойство биссектрис противолежащих углов параллелограмма.
Биссектрисы параллелограмма
Если биссектрисы углов параллелограмма, прилежащих к одной стороне перпендикулярны, то биссектрисы противолежащих углов обладают другим свойством.
Свойство биссектрис противоположных углов параллелограмма.
Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой.
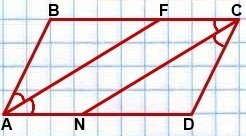
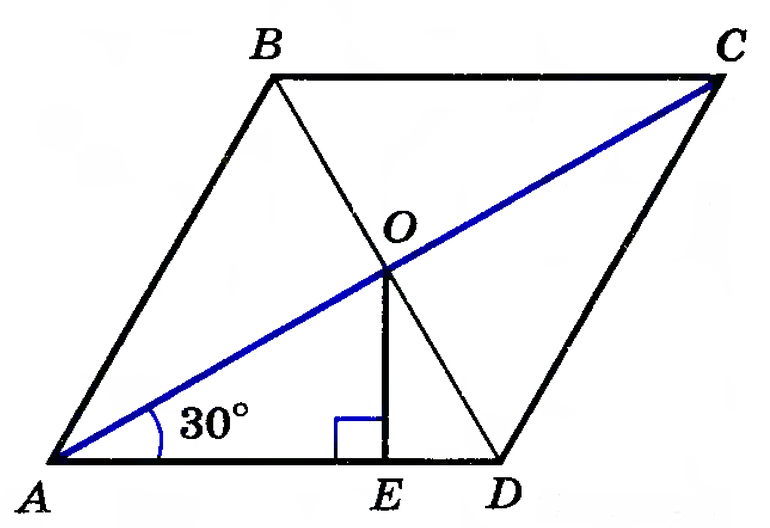
Дано: ABCD — параллелограмм,
AF — биссектриса ∠BAD,
CN- биссектриса ∠BCD.
Доказать: AF ∥ CN или лежат на одной прямой.
1) Так как AF — биссектриса ∠BAD, CN — биссектриса ∠BCD (по условию), то
Следовательно, их половины тоже равны: ∠FAD=∠BCN.
при BC ∥ AD и секущей BC).
А так как эти углы — соответственные при прямых AF и CN и секущей BC, то AF ∥ CN (по признаку параллельности прямых).
Если все стороны параллелограмма равны, биссектрисы противоположных углов лежат на одной прямой.
В этом случае из того, что AB=BC следует, что треугольник ABC — равнобедренный с основанием AC,
а значит, ∠BAC=∠BCA (как углы при основании равнобедренного треугольника).
Параллелограмм: свойства и признаки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
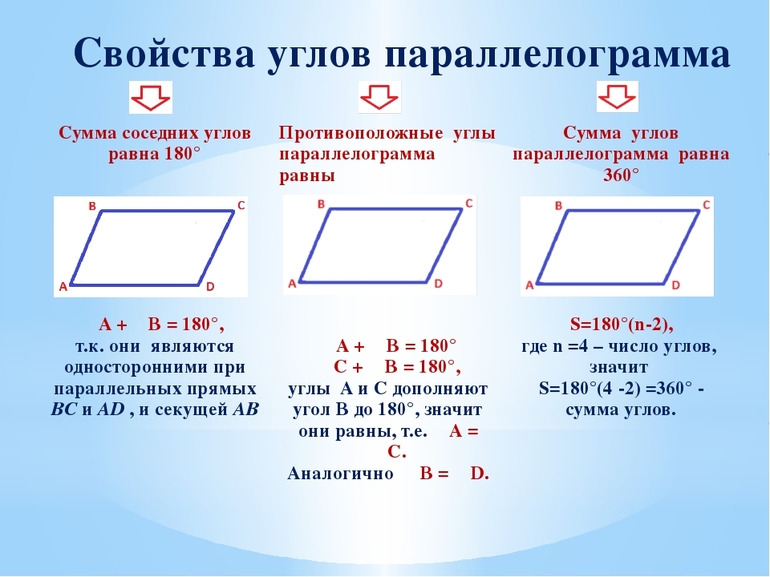
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Биссектриса параллелограмма — свойства, признаки и теоремы
Аксиома параллельности прямых, которая приведена Евклидом в книге «Начала», служит основой для доказательства многих свойств биссектрисы параллелограмма. О них знали пифагорейцы. Но понятие о самой фигуре ввел именно Евклид. Она представляет собой четырехугольник с параллельными противоположными сторонами.
Равнобедренный треугольник в параллелограмме
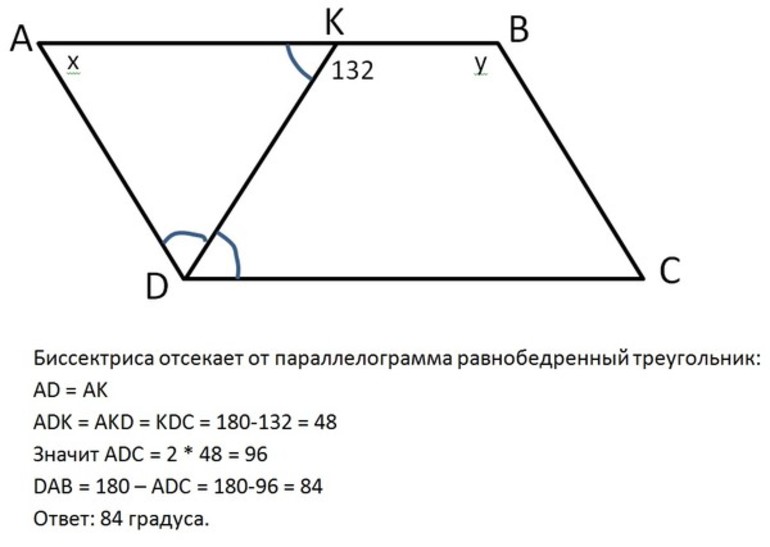
Биссектриса параллелограмма может быть проведена из вершины острого или тупого угла фигуры. Доказательство теоремы о равнобедренности образуемых прямой треугольников в этих случаях имеет аналогичный порядок. Чтобы доказать утверждение, нужно знать признак равнобедренности треугольника:
С помощью аналогичных рассуждений можно доказать, что биссектриса тупого угла параллелограмма делит противоположную сторону на отрезки и отсекает от него равнобедренный треугольник.
Точка пересечения прямых
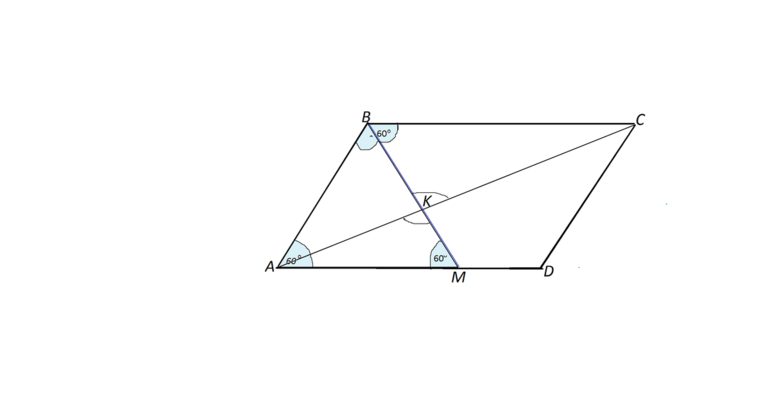
Согласно свойству, проведенные из смежных углов параллелограмма биссектрисы пересекаются в точке на противоположной стороне, если она в 2 раза больше меньшей. Доказать это утверждение можно следующим способом:
Доказательство свойства позволяет предположить, что биссектрисы смежных углов пересекаются внутри либо вне параллелограмма. При этом одна сторона больше или меньше половины другой. Если ее величина больше половины соседней, значит прямые пересекутся внутри фигуры.
Биссектрисы, проведенные через смежные углы, пересекаются с продолжением противоположных сторон параллелограмма в вершинах ромба. В зависимости от величины другой стороны, ромб совпадает с ним либо обладает большим или меньшим периметром. Если частить с построением этой фигуры, то длины сторон параллелограмма будут бесконечными.
Свойства односторонних углов
Параллелограмм АВСД имеет смежные углы при параллельных прямых АВ и СД, обозначенные а1 и а2. Для доказательства теоремы о перпендикулярности биссектрис нужно знать свойства смежных углов, сумма которых равна 180 градусам.
Поскольку биссектрисы можно провести внутри острого или тупого угла параллелограмма, то величину смежного с ним внешнего угла можно сложить, получив 180 градусов. Если обозначить их через АО и ДЕ, то углы ОАВ и ЕДС будут равны половинам а1 и а2 соответственно. Так как а1 + а2 = 180, то (а1 + а2) / 2 = 90, значит АО и ДЕ образуют прямой угол АКД.
Применять свойство биссектрис можно при нахождении периметра фигуры. Должны быть известны данные о соотношениях или длинах отрезков, образованных при пересечении противолежащей стороны биссектрисой. Например, она делит на отрезки ВК и КС сторону параллелограмма ABCD, величины которых известны.
Формула определения периметра будет иметь вид: P=2 (n+n+m). Где ВС=BК+КC=n+m, а АВ=ВК=n по свойству биссектрисы. С учетом признака равнобедренности треугольника можно построить эту прямую, дополнив рисунок фигуры без транспортира с помощью циркуля.
Противолежащие углы и биссектрисы
Согласно свойству параллельных прямых, биссектрисы a и b проходят параллельно друг другу. Они образуют внутри фигуры со сторонами mnkp другой параллелограмм, следовательно, он обладает параллельными противоположными сторонами. Прямые, на которых они лежат, соответствуют сторонам исходной фигуры, поэтому ее биссектрисы a и b являются равными.
Углы, которые образованы отрезками a и m, а также b и k, согласно свойствам биссектрис и параллелограммов, равны. Противолежащие равные по величине углы, образованные отрезками mp и nk, можно разделить пополам. Прямая b, пересекающая отрезки n и p, образует с ними накрест лежащие углы, признак которых состоит в их равенстве. Они равны разделенным пополам противоположным и являются соответственными при параллельных прямых n и p.
Вершины образуемого прямоугольника
Биссектрисы параллелограмма пересекаются в точках, представляющих собой вершины прямоугольника, что можно доказать следующим образом:
Аналогичным способом можно доказать параллельность других сторон прямой СД. Следовательно, диагональ КР образованного биссектрисами параллелограмма прямоугольника КМРО содержит точки Х и Т. Доказательство предполагает следующее равенство: КР = КХ + ХТ + ТР = ХС + СД + ТД = ВС + СД, поэтому величина диагонали равна сумме двух смежных сторон параллелограмма.
Ромб и его диагонали
Параллелограмм, имеющий биссектрису, которая совпадает с его диагональю, представляет собой ромб. Чтобы доказать это, нужно провести диагональ AC, соединяющую противоположные вершины ABCD. Способ доказательства теоремы основан на равенстве противолежащих углов параллелограмма.
Согласно свойству биссектрисы, отрезок АС делит пополам углы BCD и BAD. Они имеют одинаковую величину, поскольку противоположные углы равны. Диагональ АС — основание треугольников ACB и ACD. Согласно признаку равнобедренности АВ и АС, а также AD и CD, равны между собой. По свойству равенства противоположных сторон параллелограмма AB = CD и AD = BC.
Фигура ABCD, представляющая собой по условию параллелограмм, имеет равные по величине AB, AD, BC и CD в соответствии с доказательством. Отсюда следует, что параллелограмм ABCD по определению ромб. В нем биссектриса АС — это его диагональ.
Примеры решения задач
Биссектрисы смежных углов параллелограмма пересеклись в точке на его противолежащей стороне. Зная его меньшую сторону, можно найти большую, а также наоборот. Допустим, что длина меньшей стороны фигуры составляет 5 сантиметров.
Обозначив вершины фигуры A, B, C, D, а точку на AD буквой Р, достаточно иметь в виду, что AD=AР+РD=AB+CD. Это доказывает признак равенства накрест лежащих углов СВР и АРВ, а также ВСР и СРD при параллельных прямых. Формула для нахождения большей стороны будет иметь вид: AD=2AB=10, поскольку AB = CD. При необходимости найти меньшую можно по формуле: AD=AB/2.
По условию задачи биссектриса, исходящая из острого угла параллелограмма, разделяет его противоположную сторону на отрезки 73 мм и 54 мм, если считать от вершины тупого угла. Требуется вычислить периметр параллелограмма ABCD. Точка Е делит сторону ВС на отрезки заданной длины, поскольку АЕ — биссектриса угла ВАD. Эта прямая представляет собой секущую для параллельных AD и BC.
Отсекая равнобедренный треугольник АВЕ, биссектриса ВЕ является его основанием, поэтому сторона параллелограмма АВ равна отрезку ВЕ, длина которого по условию 73 мм. В сумме ВЕ и ЕС равны ВС, что составляет 127 мм. Отсюда периметр ABCD соответствует удвоенной сумме его сторон: Р = 2 (73+127) = 400 мм. Чтобы найти большую сторону параллелограмма ABCD при известном периметре 128 мм, можно использовать аналогичное доказательство равнобедренности треугольника.
По условию соотношение отрезков, образуемых точкой пересечения биссектрисы DЕ с противоположной стороной ВС, равно 4:3, если считать от острого угла при вершине А. Из равенства противоположных сторон ABCD и признака равнобедренного треугольника следует AD=BC=АЕ=4х, а ЕВ=3х, поэтому CD=АЕ+ЕВ=4х+3х=7х. Зная периметр ABCD, можно составить уравнение Р=2 (7х+4х)=128. Отсюда 22х=128, а х=32, поэтому большая сторона параллелограмма CD=32*7=224 мм.
Равнобедренный треугольник в параллелограмме
Биссектриса параллелограмма может быть проведена из вершины острого или тупого угла фигуры. Доказательство теоремы о равнобедренности образуемых прямой треугольников в этих случаях имеет аналогичный порядок. Чтобы доказать утверждение, нужно знать признак равнобедренности треугольника:
С помощью аналогичных рассуждений можно доказать, что биссектриса тупого угла параллелограмма делит противоположную сторону на отрезки и отсекает от него равнобедренный треугольник.
Точка пересечения прямых
Согласно свойству, проведенные из смежных углов параллелограмма биссектрисы пересекаются в точке на противоположной стороне, если она в 2 раза больше меньшей. Доказать это утверждение можно следующим способом:
Доказательство свойства позволяет предположить, что биссектрисы смежных углов пересекаются внутри либо вне параллелограмма. При этом одна сторона больше или меньше половины другой. Если ее величина больше половины соседней, значит прямые пересекутся внутри фигуры.
Биссектрисы, проведенные через смежные углы, пересекаются с продолжением противоположных сторон параллелограмма в вершинах ромба. В зависимости от величины другой стороны, ромб совпадает с ним либо обладает большим или меньшим периметром. Если частить с построением этой фигуры, то длины сторон параллелограмма будут бесконечными.
Свойства односторонних углов
Параллелограмм АВСД имеет смежные углы при параллельных прямых АВ и СД, обозначенные а1 и а2. Для доказательства теоремы о перпендикулярности биссектрис нужно знать свойства смежных углов, сумма которых равна 180 градусам.
Поскольку биссектрисы можно провести внутри острого или тупого угла параллелограмма, то величину смежного с ним внешнего угла можно сложить, получив 180 градусов. Если обозначить их через АО и ДЕ, то углы ОАВ и ЕДС будут равны половинам а1 и а2 соответственно. Так как а1 + а2 = 180, то (а1 + а2) / 2 = 90, значит АО и ДЕ образуют прямой угол АКД.
Применять свойство биссектрис можно при нахождении периметра фигуры. Должны быть известны данные о соотношениях или длинах отрезков, образованных при пересечении противолежащей стороны биссектрисой. Например, она делит на отрезки ВК и КС сторону параллелограмма ABCD, величины которых известны.
Формула определения периметра будет иметь вид: P=2 (n+n+m). Где ВС=BК+КC=n+m, а АВ=ВК=n по свойству биссектрисы. С учетом признака равнобедренности треугольника можно построить эту прямую, дополнив рисунок фигуры без транспортира с помощью циркуля.
Противолежащие углы и биссектрисы
Согласно свойству параллельных прямых, биссектрисы a и b проходят параллельно друг другу. Они образуют внутри фигуры со сторонами mnkp другой параллелограмм, следовательно, он обладает параллельными противоположными сторонами. Прямые, на которых они лежат, соответствуют сторонам исходной фигуры, поэтому ее биссектрисы a и b являются равными.
Углы, которые образованы отрезками a и m, а также b и k, согласно свойствам биссектрис и параллелограммов, равны. Противолежащие равные по величине углы, образованные отрезками mp и nk, можно разделить пополам. Прямая b, пересекающая отрезки n и p, образует с ними накрест лежащие углы, признак которых состоит в их равенстве. Они равны разделенным пополам противоположным и являются соответственными при параллельных прямых n и p.
Вершины образуемого прямоугольника
Биссектрисы параллелограмма пересекаются в точках, представляющих собой вершины прямоугольника, что можно доказать следующим образом:
Аналогичным способом можно доказать параллельность других сторон прямой СД. Следовательно, диагональ КР образованного биссектрисами параллелограмма прямоугольника КМРО содержит точки Х и Т. Доказательство предполагает следующее равенство: КР = КХ + ХТ + ТР = ХС + СД + ТД = ВС + СД, поэтому величина диагонали равна сумме двух смежных сторон параллелограмма.
Ромб и его диагонали
Параллелограмм, имеющий биссектрису, которая совпадает с его диагональю, представляет собой ромб. Чтобы доказать это, нужно провести диагональ AC, соединяющую противоположные вершины ABCD. Способ доказательства теоремы основан на равенстве противолежащих углов параллелограмма.
Согласно свойству биссектрисы, отрезок АС делит пополам углы BCD и BAD. Они имеют одинаковую величину, поскольку противоположные углы равны. Диагональ АС — основание треугольников ACB и ACD. Согласно признаку равнобедренности АВ и АС, а также AD и CD, равны между собой. По свойству равенства противоположных сторон параллелограмма AB = CD и AD = BC.
Фигура ABCD, представляющая собой по условию параллелограмм, имеет равные по величине AB, AD, BC и CD в соответствии с доказательством. Отсюда следует, что параллелограмм ABCD по определению ромб. В нем биссектриса АС — это его диагональ.
Примеры решения задач
Биссектрисы смежных углов параллелограмма пересеклись в точке на его противолежащей стороне. Зная его меньшую сторону, можно найти большую, а также наоборот. Допустим, что длина меньшей стороны фигуры составляет 5 сантиметров.
Обозначив вершины фигуры A, B, C, D, а точку на AD буквой Р, достаточно иметь в виду, что AD=AР+РD=AB+CD. Это доказывает признак равенства накрест лежащих углов СВР и АРВ, а также ВСР и СРD при параллельных прямых. Формула для нахождения большей стороны будет иметь вид: AD=2AB=10, поскольку AB = CD. При необходимости найти меньшую можно по формуле: AD=AB/2.
По условию задачи биссектриса, исходящая из острого угла параллелограмма, разделяет его противоположную сторону на отрезки 73 мм и 54 мм, если считать от вершины тупого угла. Требуется вычислить периметр параллелограмма ABCD. Точка Е делит сторону ВС на отрезки заданной длины, поскольку АЕ — биссектриса угла ВАD. Эта прямая представляет собой секущую для параллельных AD и BC.
Отсекая равнобедренный треугольник АВЕ, биссектриса ВЕ является его основанием, поэтому сторона параллелограмма АВ равна отрезку ВЕ, длина которого по условию 73 мм. В сумме ВЕ и ЕС равны ВС, что составляет 127 мм. Отсюда периметр ABCD соответствует удвоенной сумме его сторон: Р = 2 (73+127) = 400 мм. Чтобы найти большую сторону параллелограмма ABCD при известном периметре 128 мм, можно использовать аналогичное доказательство равнобедренности треугольника.
По условию соотношение отрезков, образуемых точкой пересечения биссектрисы DЕ с противоположной стороной ВС, равно 4:3, если считать от острого угла при вершине А. Из равенства противоположных сторон ABCD и признака равнобедренного треугольника следует AD=BC=АЕ=4х, а ЕВ=3х, поэтому CD=АЕ+ЕВ=4х+3х=7х. Зная периметр ABCD, можно составить уравнение Р=2 (7х+4х)=128. Отсюда 22х=128, а х=32, поэтому большая сторона параллелограмма CD=32*7=224 мм.