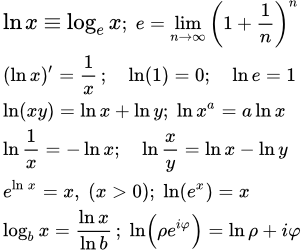К чему стремится логарифм

Формулы и свойства логарифмов

Определение логарифма

Логарифм — это математическая функция, основанная на свойствах возведения в степень.

Основываясь на математических формулах логарифмов, можно вычислить постоянную константу, которая в корреляции со всеми математическими константами окажет влияние на конечный результат логарифма числа. В месте с тем, этот результат приведет к трансформации объектов, равных пропорции необходимых логарифмов в пересчете на множители обратных функций.

С первого взгляда это сложно понять, но если увеличить коэффициент логарифма на равный ему множитель, то получится свойство логарифма применимое к школьной программе старших классов, а также для учащихся высших учебных заведений.

Категорическое решение логарифмов, основываясь на из свойствах, ставит в пропорцию их виды. Таким образом, формулы логарифмов соотносятся к самим логарифмам, как необходимая часть их самих.

Виды логарифмов

Для определения основания логарифма необходимо сначала определить его вид и, исходя из полученных результатов, по формуле и таблице сравнить корректность полученных значений. Это и будет основанием логарифма.

Чтобы решить логарифм необходимо понять, что a в степени x будет равно b, т.е. в какую степень x необходимо возвести основание логарифма a, чтобы получить значение b.

Примеры логарифмов:

В данных примерах можно увидель сложные и простые логарифмы, решение которых показывает, что всякий тождественный логарифм находится в пропорции его основания, за исключением вводных данных.

Конечно, основание логарифма пропорционально его значению, что приводит к равенству обратного значения. Это также необходимо учесть при рассмотрении равенства, кроме случаев, когда логарифм переностися с левой части равенства в правую.

log 2 8 = 3 (логарифм 8 по основанию 2 ), так как 2 3 = 8

log 7 49 = 2 (логарифм 49 по основанию 7 ), так как 7 2 = 49

Десятичный логарифм

Десятичный логарифм — логарифм по основанию 10.

Десятичный логарифм может быть не только как равенство степеней, но и показывать их различия. Наиболее хорошо это видно при разложении логарифма на члены в качестве констант a и b.

Конечным результатом решения десятичного логарифма является его сходство с натуральным логарифмом.

Примеры десятичных логарифмов:

lg 100 = 2 — десятичный логарифм обозначается именно так (lg), это десятичный логарифм ста;

Натуральный логарифм

При решении натурального логарифма его основа будет схожей с десятичным логарифмом за исключением того, что вместо числа 10 будет использоваться постоянная константа e.

Ещё одной особенностью натурального логарифма будет его неравенство по отношению к обратной функции.

Но стоит не приравнивать такое основание логарифма к прямой константе из-за большой разности при выборе метода подсчета логарифма.

Формулы и свойства логарифмов

Именно это свойство логарифмов позволяет вычислять точные значения в отличае от других методов вычисления.

Неточность других методов вычисления основывается на неверной корреляции остаточного члена логарифмического равенства.

Наряду с этим каждое из свойств является индивидуальным, равно как каждый из его членов. Всё это позволяет сделать вывод, что благодаря формулам, выведенным математиком, вычисления становятся простыми в рамках неравенств.

Основное логарифмическое тождество

Логарифм единицы

Вычисления такого логарифма применяются в балистике при расчете траектории движения объекта, находящегося в непосредственной близости от Земли. Это обусловлено наиболее точным значением ускорением свободного падения, равным 9,81. А при удалении от поверности Земли это значение изменяется, уменьшается пропорционально расстоянию удаления от поверхности.

Логарифм числа, равного основанию

Логарифмическая единица. Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.

Логарифм числа, обратного основанию

Логарифм произведения двух положительных чисел

Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2-х логарифмов, у которых будут одинаковые основания.

Логарифм частного

Логарифм частного. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.

Логарифм степени положительного числа

Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.

Логарифм корня числа

Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.

Основание логарифма в степени

Формула перехода к новому основанию

log a x = log b x log b a

log a x = 1 log x a

Производная логарифма

Производная логарифмической функции по основанию равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.

При расчёте производной логарифма необходимо учитывать ложный коэффициент производной, при котором нарастает его гиперболическая составляющая. Это и есть главное условие корректного нахождения производной логарифма. В то же время, нельзя упускать второстепенные составляющие при расчёте. К ним относятся расчеты с применением общей суммы логарифмов, а также пропорциональная составляющая двух вычисляемых логарифмов. Такой подход можно применить не только для вычисления производной натурального логарифма, но и при расчете производной десятичного логарифма при возведении в степень x по основанию a.

График логарифмов

Таким образом можно увидеть изменения логарифма по основанию от 0 до 10. Промежуточным результатом является логарифм по основанию e, которое приблизительно равно 2.72.

Так трафик логарифма по основанию 0 имеет форму прямой линии, а графики десятичного логарифма и натурального логарифма имею гиперболическую форму.

Источник

Натуральный логарифм, функция ln x

Определение

Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045. ;
.

График натурального логарифма ln x

При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.

Область определения	0
Область значений	– ∞
Монотонность	монотонно возрастает
Нули, y = 0	x = 1
Точки пересечения с осью ординат, x = 0	нет
+ ∞
– ∞

Значения ln x

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе «Логарифм».

Обратная функция

Обратной для натурального логарифма является экспонента.

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Выражения через комплексные числа

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Источник

Логарифм. Натуральный логарифм.

За основание логарифмов нередко берут цифру е = 2,718281828. Логарифмы по данному основанию именуют натуральным. При проведении вычислений с натуральными логарифмами общепринято оперировать знаком ln, а не log; при этом число 2,718281828, определяющие основание, не указывают.

Само число е определяет предел монотонной ограниченной последовательности

Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!

На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.

График натурального логарифма (функции y = ln x) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:

Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a.

Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».

Если анализировать натуральный логарифм, как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:

По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:

Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.

Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x. Он монотонно возрастает на своей области определения.

При x →0 пределом натурального логарифма выступает минус бесконечность ( –∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.

Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.

Источник

Логарифмы

Определение логарифма

Понятие логарифма и основного логарифмичесгого тождества

Понятие логарифма и основного логарифмическое тождества состоят в тесной зависимости, т.к. определение логарифма в математической записи и является основным логарифмическим тождеством.

Основное логарифмическое тождество вытекает из определения логарифма:

Логарифмом называют показатель степени n, при возведении в которую числа а получают число b.

Показательное уравнение a^n=b при a > 0, a ne 1 не имеет решений при неположительном b и имеет единственный корень при положительном b. Этот корень называется логарифмом числа b по основанию а и записывают:

Основное логарифмическое тождество

4 log₂ 7 =2 2 log₂ 7 = (2 log₂ 7 ) 2 = 7 2 = 49

2 1 + log₂ 7 = 2 · 2 log₂ 7 = 2 · 7 = 14

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X. и преобразовываем в и преобразовываем в Запомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Два очевидных следствия определения логарифма

log a 1 = 0 ( a > 0, a ≠ 1 )

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.

Логарифм. Свойства логарифма (корень логарифма, смена основания).

Корень логарифма из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня/Логарифм. Свойства логарифма (корень логарифма, смена основания).

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.

Например, если при решении уравнения или неравенства требуется преобразовать выражение

следует применять формулу

поскольку в противном случае можно потерять корни.

По той же причине при преобразовании выражений

log_a ( f (x) g (x)) и

следует использовать формулы:

Степень можно выносить за знак логарифма

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a ( f ( x ) 2 = 2 log a f ( x )

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Виды логарифмов

log_a b – логарифм числа b по основанию a ( a > 0, a ≠ 1, b > 0)

lg b – десятичный логарифм (логарифм по основанию 10, a = 10).

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать: Логарифмы с одинаковыми основаниями можно вычитать: Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма: Подставим полученные результаты в исходное выражение:

Десятичные и натуральные логарифмы

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log₁₀x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например,

lg ( x y ) = lg x + lg y ( x > 0, y > 0 )

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e – иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:

log a b = lg b lg a = ln b ln a ( a > 0, a ≠ 1, b > 0 )

Вычисление логарифма равносильно решению показательного уравнения

при условии a > 0, a ≠ 1; b > 0, где

при условии a > 0, a ≠ 1; b > 0, где

Найти логарифм: log ₄ 8

Обозначим log₄ 8 через x :

Перейдем к показательному уравнению:

Сведем показательное уравнение к основе 2 и решим его:

Найти x если : log _x 125 = 3 2

За определением логарифма имеем:

x = (5 3 ) 2/3 = 5 3·2/3 = 5 2 = 25

Формулировки и доказательства свойств

Покажем примеры использования свойства логарифма произведения: log₅(2·3)=log₅2+log₅3 и .

Приведем пример использования этого свойства логарифма: .

Вот пример использования этого свойства: .

Покажем пару примеров применения этого свойства логарифмов: и .

Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a : .

Осталось доказать свойства сравнения логарифмов.

Область допустимых значений (ОДЗ) логарифма

Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).

Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:

Поэтому и отрицательные основания проще выбросить, чем возиться с ними.

Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:

Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?

– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».

Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:

10 примеров логарифмов с решением

1. Найти значение выражения 2. Найти значение выражения 3. Найти значение выражения 3. Найти значение выражения 4. Найти значение выражения 5. Найти значение выражения 5. Найти значение выражения 6. Найти значение выражения Сначала найдем значение Сначала найдем значение Для этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выражения 7. Найти значение выражения Преобразуем наше выражение: Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выражения 8. Найти значение выражения Так как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов: 9. Найти значение выражения 9. Найти значение выражения Так как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выражения Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄: Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник