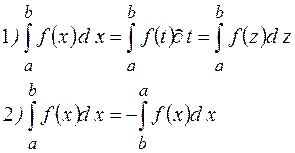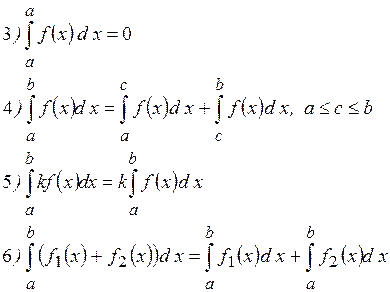физические приложения неопределенного интеграла

Тема 1.3. Интеграл и его приложения

В рекомендуемых учебных пособиях необходимо ознакомиться со следующими краткими сведениями справочного характера по интегральному исчислению.

-понятие первообразной данной функции;

— определение неопределенного интеграла;

— основные свойства неопределенного интеграла;

— таблица основных неопределённых интегралов;

— применение основных свойств и таблицы неопределенных интегралов, непосредственное интегрирование;

— определение и свойства определенного интеграла;

— определённый интеграл как площадь криволинейной трапеции, его принципиальное отличие от неопределенного интеграла;

— вычисление определённого интеграла. Формула Ньютона-Лейбница.

— замена переменной в определенном интеграле;

— вычисление площадей плоских фигур и объёмов тел вращения;

— использование определенного интеграла при решении задач прикладного характера.

В результате изучения темы студент должен:

Уметь:

— находить неопределённые интегралы, сводящиеся к табличным, с помощью основных свойств и простых преобразований;

— восстанавливать закон движения по заданной скорости, скорость по ускорению, количество электричества по силе тока и др.;

— вычислять определённый интеграл с помощью основных его свойств и формулы Ньютона-Лейбница;

— находить площади криволинейных трапеций;

— решать простейшие прикладные задачи, сводящиеся к составлению и вычислению интеграла.

использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:

— решения прикладных задач на вычисление в простейших случаях площадей и объемов с использованием определенного интеграла;

Приведём основные свойствами неопределенного интеграла:

1) постоянный множитель (к¹0) можно выносить за знак интеграла:

.

2) интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций

.

3) или .

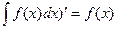
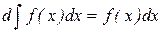
4) или .

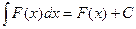
5) .

Основные формулы интегрирования

Приведем таблицу основных неопределенных интегралов:

;

;

;

;

;

;

;

;

;

;

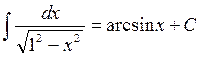
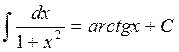
Справедливость этих формул можно проверить путем дифференцирования, т.е. легко убедиться в том, что производные от правых частей формул

будут равны соответствующим подынтегральным функциям. Интегралы таблицы называются табличными.

Основные методы интегрирования.

Непосредственное интегрирование – это такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Интегрирование методом подстановки (замены переменной).

Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае используют метод подстановки. Для интегрирования методом постановки будем использовать следующую схему:

1. Часть подынтегральной функции заменим новой переменной;

2. Найдем дифференциал от обеих частей замены;

3. Выразим подынтегральное выражение через новую переменную (после чего должен получиться табличный интеграл);

4. Найдем полученный табличный интеграл;

5. Сделаем обратную замену, вернемся к старой переменной.

Определение. Если -первообразная функция для , то приращение первообразных функций при изменении аргумента от до называется определенным интегралом и обозначается

т.е.

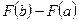
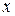
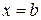
Непосредственное вычисление определенного интеграла

В отличие от неопределенного интеграла, представляющего собой совокупность всех первообразных от данной функции, определенный интеграл есть число. Для его вычисления применяют формулу Ньютона- Лейбница

где — нижний, а — верхний пределы определенного интеграла.

Т. е. значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции при нижнем и верхнем пределах интегрирования. Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов.

Если функция положительна, то определенный интеграл представляет собой площадь криволинейной трапеции (фигура, ограниченная графиком непрерывной функции , , прямыми и отрезком оси Ox). В этом заключается геометрический смысл определенного интеграла. Таким образом, площадь криволинейной трапеции можно вычислить по формуле: .

Основные свойства определенного интеграла

Вопросы для самоконтроля

1. Какая связь существует между операциями дифференцирования и интегрирования?

2. Какая функция называется первообразной для заданной функции?

3. Дайте определение неопределенного интеграла.

4. Назовите основные свойства неопределенного интеграла.

5. Перечислите основные табличные интегралы.

6. Запишите формулу Ньютона- Лейбница.

7. Объясните, почему она называется формулой, выражающей связь определённого интеграла с неопределённым? Где в ней неопределённый интеграл?

8. В чём принципиальное различие неопределённого и определённого интегралов?

9. Какую фигуру называют криволинейной трапецией?

10. Запишите формулу для вычисления площади криволинейной трапеции.

11. В чем заключается геометрический смысл определённого интеграла?

12. Запишите основные свойства определенного интеграла.

13. Какие методы вычисления определенного интеграла Вам известны?

14. Назовите несколько примеров применения определенного интеграла в геометрии и физике.

Источник

Физические приложения неопределенного интеграла. Физические приложения определенного интеграла

41.1. Схемы применения определенного интеграла

Пусть требуется найти значение какой-либо геометрической или физической величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком изменения независимой переменной х. Предполагается, что эта величина А аддитивна, т. е. такая, что при разбиении отрезка [а; b] точкой с є (а; b) на части [а; с] и [с; b] значение величины А, соответствующее всему отрезку [а; b], равно сумме ее значений, соответствующих [а; с] и [с; b].

Для нахождения этой величины А можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).

Первая схема базируется на определении определенного интеграла.

2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: ΔA i ≈ ƒ(c i)Δx i.

При нахождении приближенного значения ΔА i допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д.

Получим приближенное значение величины А в виде интегральной суммы:

3. Искомая величина А равна пределу интегральной суммы, т. е.

Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых.

Схема I была применена для выяснения геометрического и физического смысла определенного интеграла.

Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:

2) находим главную часть приращения ΔА при изменении х на малую величину Δх = dx, т. е. находим дифференциал dA функции А = А(х): dA = ƒ(х) dx, где ƒ(х), определяемая из условия задачи, функция переменной х (здесь также возможны различные упрощения);

3) считая, что dA ≈ ΔА при Δх → 0, находим искомую величину путем интегрирования dA в пределах от а до b:

41.2. Вычисление площадей плоских фигур

Как уже было установлено (см. «геометрический смысл определенного интеграла»), площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному интегралу:

Для нахождения площади S этой трапеции проделаем следующие операции:

1. Возьмем произвольное х Î [а; b] и будем считать, что S = S(x).

2. Дадим аргументу х приращение Δх = dx (х + Δх є [а; b]). Функция S = S(x) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).

Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у dx.

3. Интегрируя полученное равенство в пределах от х = а до х = b,получаем

Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) ≤ φ ≤ β (если φ = а, то S(a) = 0, если φ=β, то S(β) = S).

2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.

Дифференциал dS представляет собой главную часть приращения ΔS при dφ → 0 и равен площади кругового сектора О АС (на рисунке она заштрихована) радиуса r с центральным углом dφ. Поэтому

3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь

Пример 41.3. Найти площадь фигуры, ограниченной «трехлепесткoвой розой» r=acos3φ (см. рис. 181).

Решение: Найдем сначала площадь половины одного лепестка «розы», т. е.1/6 часть всей площади фигуры:

Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке 182, имеем:

41.3. Вычисление длины дуги плоской кривой

Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у» = ƒ»(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).

Таким образом,или в сокращенной записи l =

Еслиуравнение кривой АВ задано в параметрической форме

Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x»(t)dt,

Пример 41.4. Найти длину окружности радиуса R.

Решение: Найдем 1/4 часть ее длины от точки (0;R)до точки (R;0) (см. рис. 184). Так как то

Значит, l = 2π R. Если уравнение окружности записать в параметрическом виде х=Rcost, у = Rsint (0≤t≤2π ), то

Вычисление длины дуги может быть основано на применении метода дифференциала. Покажем, как можно получить формулу (41.3), применив схему II (метод дифференциала).

1. Возьмем произвольное значение х є [а; b] и рассмотрим переменный отрезок [а;х]. На нем величина l становится функцией от х, т.е. l = l (х) (l (а) = 0 и l (b) = l ).

3. Интегрируя dl в пределах от а до b, получаем

Равенствоназываетсяформулой дифференциала дуги в прямоугольных координатах.

Последняя формула представляет собой теорему Пифагора для бесконечно малого треугольника МСТ (см. рис. 186).

Пусть кривая АВ задана уравнением в полярных координатах r = r(φ), а≤φ≤β. Предположим, что r(φ) и r»(φ) непрерывны на отрезке [а;β].

Если в равенствах х = rcosφ, у = rsinφ, связывающих полярные и декартовы координаты, параметром считать угол φ, то кривую АВ можнозадать параметрически

Применяя формулу (41.5), получаем

Пример 41.5. Найти длину кардиоиды r = = а(1 + cosφ).

Решение: Кардиоида r = а(1 + cosφ) имеет вид, изображенный на рисунке 187. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:

Таким образом, 1/2l= 4а. Значит, l= 8а.

41.4. Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.

1. Через произвольную точку х є проведем плоскость ∏, перпендикулярную оси Ох (см. рис. 188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; х] величина v есть функция от х, т. е. v = v(x) (v(a) = 0, v(b) = V).

2. Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х+Δх, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(x) dx.

3. Находим искомую величину V путем интегрирования dA в пределах от а до В:

Полученная формула называется формулой объема тела по площади параллельных сечений.

Решение: Рассекая эллипсоид плоскостью, параллельной плоскости Oyz и на расстоянии х от нее (-а ≤х≤ a), получим эллипс (см. рис. 189):

Площадь этого эллипса равна

Поэтому, поформуле (41.6), имеем

Объем тела вращения

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х) 0, отрезком а ≤ x ≤ bи прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х Î [а; b]), есть круг с радиусом у= ƒ(х). Следовательно, S(x)= π y 2.

Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком не прерывной функциих=φ(у) ≥ 0 и прямыми х = 0, у = с,

3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем

Пример 41.8. Найти площадь поверхности шара радиуса R.

Пример 41.9. Дана циклоида

Найти площадь поверхности, образованной вращением ее вокруг оси Ох.

Решение: При вращении половины дуги циклоиды вокруг оси Ох площадь поверхности вращения равна

41.6. Механические приложения определенного интеграла

Работа переменной силы

Таким образом, dp=gg π R 2 dx и dA = gg π R 2 dx*x.

3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим

Путь, пройденный телом

Отметим, что эту же формулу можно получить, пользуясь схемой I или II применения определенного интеграла.

Пример 41.12. Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела v(t) = 10t + 2 (м/с).

Решение: Если v(t)=10t+2 (м/с), то путь, пройденный телом от начала движения (t=0) до конца 4-й секунды, равен

Давление жидкости на вертикальную пластинку

По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.

Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у 1 = f 1 (x) и у 2 =ƒ 2 (х); система координат выбрана так, как указано на рисунке 194. Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала).

Тогда по закону Паскаля

3. Интегрируя полученное равенство в пределах от х = а до х = В, получим

Пример 41.13. Определить величину давления воды на полукруг, вертикально погруженный в жидкость, если его радиус R, а центр О находится на свободной поверхности воды (см. рис. 195).

Аналогично определяется статический момент S y этой системы относительно оси

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.

Для произвольного х є [а; b] на кривой АВ найдется точка с координатами (х;у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого участка равна g dl. Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента dS x («элементарный момент») будет равен g dly, т. е. dS x = g dlу (см. рис. 196).

Отсюда следует, что статический момент S x кривой АВ относительно оси Ох равен

Аналогично находим S y:

Статические моменты S x и S y кривой позволяют легко установить положение ее центра тяжести (центра масс).

Центром тяжести материальной плоской кривой у = ƒ(х), х Î называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу m заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой у = ƒ (х) относительно той же оси. Обозначим через С(х с;у с) центр тяжести кривой АВ.

Из определения центра тяжести следуют равенства Отсюда

Вычисление статических моментов и координат центра тяжести плоской фигуры

Пусть дана материальная плоская фигура (пластинка), ограниченная кривой у = ƒ(х) 0 и прямыми у = 0, х = a, x = b (см. рис. 198).

Будем считать, что поверхностная плотность пластинки постоянна (g = const). Тогда масса «всей пластинки равна g * S, т. еВыделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.

Тогда масса его равна g ydx. Центр тяжести С пря моугольника лежит на пересечении диагоналей прямоугольника. Эта точка С отстоит от оси Ох на 1/2*у, а от оси Оу на х (приближенно; точнее на расстоянии х+ 1 / 2 ∆х). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения

Итак, центр тяжести имеет координаты

Определенный интеграл (ОИ) широко используется в практических приложениях математики и физики.

В частности, в геометрии с помощью ОИ находят площади простых фигур и сложных поверхностей, объемов тел вращения и тел произвольной формы, длин кривых на плоскости и в пространстве.

В физике и теоретической механике ОИ применяют для вычисления статических моментов, масс и центров масс материальных кривых и поверхностей, для вычисления работы переменной силы по криволинейному пути и др.

Площадь плоской фигуры

Длина дуги кривой

Вычисление объема тела по площадям параллельных сечений

Объем тела вращения

Площадь поверхности тела вращения

Физические приложения ОИ

Работа переменной силы

Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F(x), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (a Выбор читателей

Источник