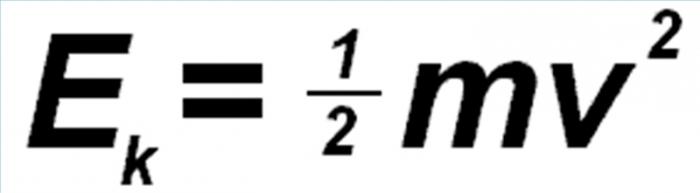что влияет на величину кинетической энергии тела

Кинетическая и потенциальная энергии

Кинетическая энергия

Работа всех сил, действующих на тело, равна работе равнодействующей силы.

Как видим, работа, совершенная силой, пропорционально изменению квадрата скорости тела.

Определение. Кинетическая энергия

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Теорема о кинетической энергии

Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела.

Теорема о кинетической энергии

Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.

Чтобы остановить тело, нужно совершить работу

Потенциальная энергия

Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.

При этом сила тяжести совершила работу, равную

Определение. Потенциальная энергия

Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

Потенциальная энергия пружины

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

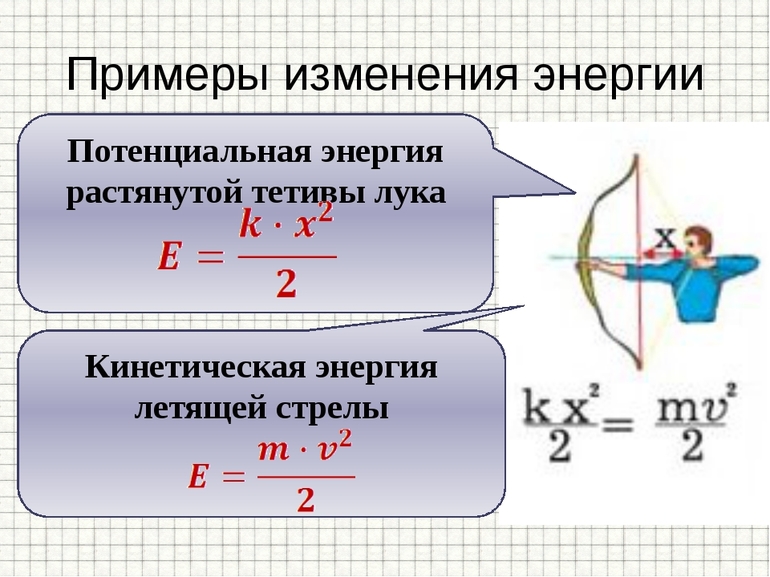
Величина E у п р = k x 2 2 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Источник

Потенциальная и кинетическая энергия позволяют охарактеризовать состояние любого тела. Если первая применяется в системах взаимодействующих объектов, то вторая связана с их движением. Эти виды энергии, как правило, рассматриваются тогда, когда сила, связывающая тела, независима от траектории движения. При этом важны только начальное и конечное их положения.

Общие сведения и понятия

Кинетическая энергия системы является одной из важнейших ее характеристик. Физики выделяют два вида такой энергии в зависимости от вида движения:

Кинетическая энергия (Е_к) представляет собой разность между полной энергией системы и энергией покоя. Исходя из этого, можно сказать, что она обусловлена движением системы. Тело имеет ее только тогда, когда оно движется. В состоянии покоя объекта она равняется нулю. Кинетическая энергия любых тел зависит исключительно от скорости движения и их масс. Полная энергия системы находится в прямой зависимости от скорости ее объектов и расстояния между ними.

Основные формулы

В том случае, когда любая сила (F) действует на тело, находящееся в покое так, что оно приходит в движение, можно говорить о совершении работы dA. При этом величина этой энергии dE будет тем выше, чем больше совершается работы. В этом случае верно такое равенство: dA = dE.

С учетом пути, пройденного телом (dR) и его скорости (dU), можно воспользоваться 2 законом Ньютона, исходя из которого: F = (dU/dE)*m.

Вышеуказанный закон используется только тогда, когда имеется инерциальная система отсчета. Существует еще один важный нюанс, учитываемый при расчетах. На значение энергии влияет выбор системы. Так, согласно системе СИ, она измеряется в джоулях (Дж). Кинетическая энергия тела характеризуется массой m, а также скоростью перемещения υ. В этом случае она составит: E_k = ((υ*υ)*m)/2.

Исходя из вышеуказанной формулы, можно сделать вывод, что кинетическую энергию определяют массой и скоростью. Иными словами, она представляет собой функцию движения тела.

Энергия в механической системе

Кинетическая энергия механической системы являет собой арифметическую сумму таких же энергий всех ее точек. Ее также можно выразить следующей формулой: E_k = 1/2Mυ c2 + Ec, где υc — скорость центра масс, М – масса системы, Ec – кинетическая энергия системы при движении вокруг центра масс.

Энергия твердого тела

Данное равенство отражает теорему, касающуюся изменения кинетической энергии. С ее помощью решаются самые разные задачи механики. Без этой формулы невозможно решить целый ряд важнейших задач.

Кинетическая энергия при высоких скоростях

Если скорости тела близки к скорости света, кинетическую энергию материальной точки можно рассчитать по следующей формуле:

Источник

Концепция и классификация

Ещё в древности энергию определяли как свойство или способность, которые тела и вещества должны производить вокруг себя и которые во время преобразований обмениваются через два механизма: в форме работы или тепла. Правда, тогда еще не знали, что таким образом выполняется закон сохранения энергии. Но кроме физических изменений, проявляющихся, например, в подъёме объекта, его транспортировке, деформации или нагревании, энергия также присутствует в химических изменениях, таких как сжигание куска дерева или разложение воды электрическим током.

Энергия — это способность тела работать, а также сила, которая выполняет работу. Она может быть представлена в виде различных переходных форм:

В физике самая важная форма называется механической энергией. Это сумма и определение потенциальной и кинетической энергии, формула которой: E = Ek + Wp.

Энергия движения

Кинетическая энергия тела — это та, которой тело обладает благодаря своему движению. Её определяют как силу, необходимую для ускорения тела определённой массы от покоя до максимальной указанной скорости. Как только достигается ускорение, тело сохраняет энергию, если скорость не изменяется. Чтобы тело вернулось в состояние покоя, необходима отрицательная работа той же величины.

Единица измерения кинетической энергии — джоуль. Обычно она обозначается буквой E c или E k. Расчёт мощности измеряется по-разному. Для того чтобы найти её количество можно использовать онлайн-калькулятор.

История и определение

Прилагательное «кинетический» в названии произошло от древнегреческого слова кίνησις kinēsis, что означает «движение».

Идею связи классической механики и кинематической энергии впервые выдвинули Готфрид Вильгельм Лейбниц и Даниэль Бернулли. Учёный Грейвсанд из Нидерландов предоставил экспериментальное подтверждение этой связи.

Но первые теоретические выкладки этих идей приписаны Гаспар-Гюстав Кориолису, который в 1829 году опубликовал статью, где была изложена математика этого процесса. Сам термин появился в 1849 году благодаря Уильяму Томсону, более известному как лорд Кельвин.

Теорема о кинетической энергии гласит: изменение кинетической силы тела равно работе равнодействующей всех сил, действующих на тело. Эта теорема справедлива независимо от того, какие силы действуют на тело.

Часто различают кинетическую силу поступательного и вращательного движения. Как и любая физическая величина, которая является функцией скорости, она не только зависит от внутренней природы этого объекта, но также зависит от отношений между объектом и наблюдателем (в физике наблюдатель формально определяется классом определённая система координат, называемая инерциальной системой отсчёта).

Эта энергия деградирует и сохраняется в каждой трансформации, теряя способность совершать новые трансформации, но она не может быть создана или разрушена, только трансформирована, поэтому её сумма во вселенной всегда постоянна.

Кинематика системы частиц

Для частицы или для твёрдого тела, которое не вращается, кинетическая энергия падает до нуля, когда тело останавливается. Однако для систем, которые содержат много частиц с независимыми движениями, это не совсем верно.

Для твёрдого тела, которое вращается, полная кинетическая сила может быть разбита на две суммы: энергия перемещения, связанная со смещением центра масс тела в пространстве, и вращения (с вращательным движением с определённой угловой скоростью).

Потенциальная энергия

Этот термин был введён в XIX веке учёным Уильямом Ренкином и связан с механической энергией, которая зависит от расположения тела в силовом поле (гравитационное, электростатическое и т. д. ) или с наличием силового поля внутри тела.

Теорема о потенциальной энергии утверждает, что она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Независимо от силы, её порождающей, потенциальная энергия, которой обладает физическая система, хранится благодаря своему положению и / или конфигурации, в чём и заключается её различие с кинетической энергией.

Значение потенциала всегда зависит от нахождения или конфигурации, выбранной для её измерения, поэтому иногда говорят, что физически имеет значение только его изменение отношений между двумя конфигурациями.

Потенциальная энергия присутствует не только в классической физике, но также в релятивистской и квантовой физике. Эта концепция также была распространена на физику элементарных частиц.

Смысл потенциальной силы связан с работой, выполняемой силами физической системы для перемещения её из одного состояния в другое. А её функция будет существенно зависеть от типа силового поля или взаимодействия, действующего на систему.

Это относится, например, к атомной физике при получении электронных состояний атома или к молекулярной физике для получения таких состояний молекулы, как:

В других более общих формулировках физики потенциальная функция также играет важную роль. Среди них лагранжева и гамильтонова формулировки механики.

Гравитационная сила

Потенциальной гравитацией обладают тела в силу того, что они имеют массу и находятся на определённом взаимном расстоянии. Среди огромных масс действуют силы притяжения. Применительно, например, к планетарному движению, основная масса солнечной системы состоит из массы Солнца, которая создаёт гравитационное силовое поле, воздействующее на малые массы планет. В свою очередь, каждая планета создаёт такое же поле, которое воздействует на второстепенные тела, находящиеся на её поверхности. Зависимость силы тяжести от высоты можно изобразить на графике. При увеличении массы тела линейно увеличивается и она.

Энергия упругой деформации

Эластичность — это свойство определённых материалов, благодаря которому, будучи деформированными, растянутыми или отделёнными от своего исходного положения, они могут восстановить своё первоначальное состояние или равновесие. Восстановительными силами, ответственными за восстановление, являются силы упругости, как в случае пружин, резиновых полос или струн музыкальных инструментов.

Многие древние военные машины использовали эти силы для запуска объектов на расстоянии, таких как дуга, которая стреляет стрелой, арбалет или катапульта. Вибрации или колебания материальных объектов, вызванные упругими силами, являются источником звуковых волн. Силы восстановления, когда объект восстанавливает свою первоначальную форму практически без какого-либо демпфирования или деформации, являются консервативными, и может быть получена упругая сила.

Пружина является примером упругого объекта, который точно восстанавливает первоначальную форму: при растяжении он создаёт упругую силу, стремящуюся вернуть его к первоначальной длине. Экспериментально подтверждено, что эта восстановительная сила пропорциональна растянутой длине пружины. Способ выразить эту пропорциональность между силой и растянутой суммой — через закон Гука.

Коэффициент пропорциональности при этой деформации зависит от типа материала и рассматриваемой геометрической формы. Для твёрдых тел сила упругости обычно описывается в терминах величины деформации, вызванной растягивающей силой, возникающей в результате этого растяжения, называемого упругостью или модулем Юнга. Для жидкостей и газов это выражается изменением давления, способного вызвать изменение объёма, и называется модулем сжимаемости.

Одним из свойств упругости твёрдого тела или жидкости при растяжении или деформации является то, что растяжение или деформация пропорциональны приложенному усилию. То есть для создания двойного растяжения потребуется двойная сила. Эта линейная зависимость смещения от приложенной силы известна как закон Гука.

Прикладное значение

Потенциальная электростатическая энергия может храниться с помощью конденсаторов. Конденсатор — это устройство, которое накапливает её внутри. Чтобы сохранить электрический заряд, он использует две проводящие поверхности, как правило, в форме листов или пластин, разделённых диэлектрическим материалом (изолятором). Эти платы являются электрически заряженными при подключении к источнику питания.

Две пластины имеют одинаковую величину, но с разными знаками, причём величина нагрузки пропорциональна приложенной разности потенциалов. Константа пропорциональности между зарядом, приобретённым конденсатором, и разностью потенциалов, достигнутой между двумя пластинами, называется ёмкостью конденсатора:

Области применения конденсаторов многочисленны в области электроники, и, следовательно, они также предназначены для бытовых приборов. В современных технологических приложениях их используют:

В этих применениях современной технологии конденсаторы способны накапливать электростатическую энергию в течение коротких периодов времени и с не слишком высокими значениями.

Источник

Потенциальная и кинетическая энергия. Закон сохранения механической энергии

1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой ​ \( E \) ​. Единица работы — ​ \( [E\,] \) ​ = 1 Дж.

При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: ​ \( E=A \) ​.

2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.

Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.

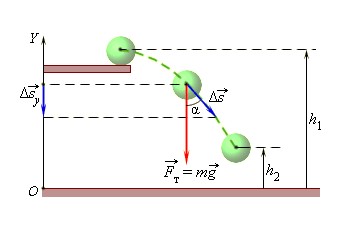
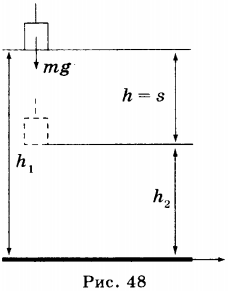
Если тело массой ​ \( m \) ​ падает с высоты ​ \( h_1 \) ​ до высоты ​ \( h_2 \) ​, то работа силы тяжести ​ \( F_т \) ​ на участке ​ \( h=h_1-h_2 \) ​ равна: ​ \( A = F_тh = mgh = mg(h_1 — h_2) \) ​ или \( A = mgh_1 — mgh_2 \) (рис. 48).

В полученной формуле ​ \( mgh_1 \) ​ характеризует начальное положение (состояние) тела, \( mgh_2 \) характеризует конечное положение (состояние) тела. Величина \( mgh_1=E_ <п1>\) — потенциальная энергия тела в начальном состоянии; величина \( mgh_2=E_ <п2>\) — потенциальная энергия тела в конечном состоянии.

Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.

Если тело находится на некоторой высоте ​ \( h \) ​ относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна ​ \( E_п=mgh \) ​. Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.

В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.

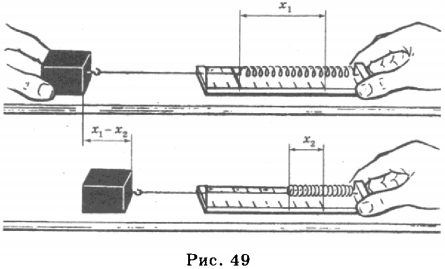
3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на ​ \( x_1 \) ​, то в пружине возникнет сила упругости ​ \( F_ <упр1>\) ​, направленная вправо (рис. 49).

Работа силы упругости равна

​ \( kx_1^2/2=E_ <п1>\) ​ — потенциальная энергия пружины в начальном состоянии, \( kx_2^2/2=E_ <п2>\) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.

Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.

Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние ​ \( x \) ​, то потенциальная энергия пружины в данном состоянии равна ​ \( E_п=kx^2/2 \) ​.

Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.

Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.

В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ​ \( m_1 \) ​ в три раза больше массы другого тела ​ \( m_2 \) ​. Относительно поверхности Земли потенциальная энергия

1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела

2. Сравните потенциальную энергию мяча на полюсе ​ \( E_п \) ​ Земли и на широте Москвы ​ \( E_м \) ​, если он находится на одинаковой высоте относительно поверхности Земли.

1) ​ \( E_п=E_м \) ​
2) \( E_п>E_м \)
3) \( E_п
4) \( E_п\geq E_м \)

3. Тело брошено вертикально вверх. Его потенциальная энергия

1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории

4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?

1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз

5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?

1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж

6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия

1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза

7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела

1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза

8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела

1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения

9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.

1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг

10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.

1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с

11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) ​ \( E=mv^2/2 \) ​
2) \( E=kx^2/2 \) ​
3) \( E=mgh \) ​

12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется

Часть 2

13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.

Источник