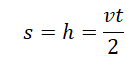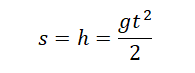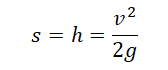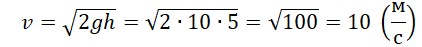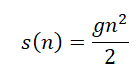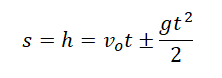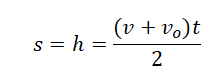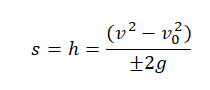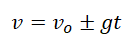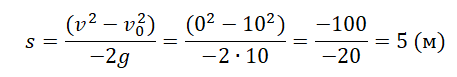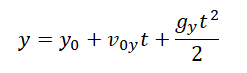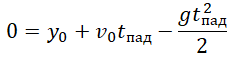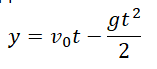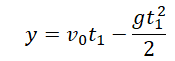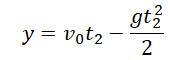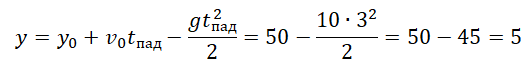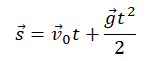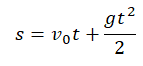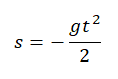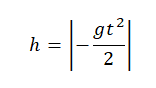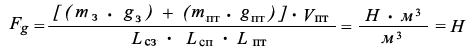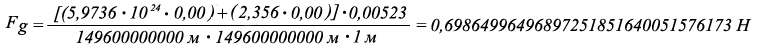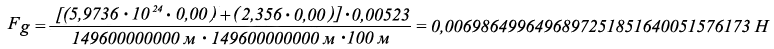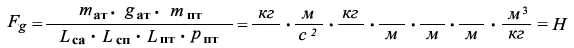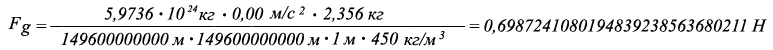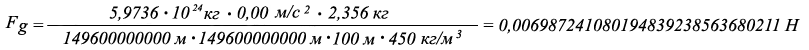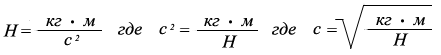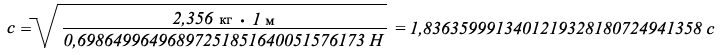что влияет на скорость падения

Определение скорости свободного падения

Свободное падение тела — это его равнопеременное движение, которое происходит под действием силы тяжести. В этот момент другие силы, которые могут воздействовать на тело либо отсутствуют, либо настолько малы, что их влияние не учитывается. Например, когда парашютист прыгает из самолета, первые несколько секунд после прыжка он падает в свободном состоянии. Этот короткий отрезок времени характеризуется ощущением невесомости, сходным с тедж.м, что испытывают космонавты на борту космического корабля.

История открытия явления

О свободном падении тела ученые узнали еще в Средневековье: Альберт Саксонский и Николай Орем изучали это явление, но некоторые их выводы были ошибочными. Например, они утверждали, что скорость падающего тяжелого предмета возрастает прямо пропорционально пройденному расстоянию. В 1545 году поправку этой ошибки сделал испанский ученый Д. Сото, установивший факт, что скорость падающего тела увеличивается пропорционально времени, которое проходит от начала падения этого предмета.

В 1590 г. итальянский физик Галилео Галилей сформулировал закон, который устанавливает четкую зависимость пройденного падающим предметом пути от времени. Также ученым было доказано, что при отсутствии воздушного сопротивления все предметы на Земле падают с одинаковым ускорением, хотя до его открытия было принято считать, что тяжелые предметы падают быстрее.

Была открыта новая величина — ускорение свободного падения, которое состоит из двух составляющих: гравитационного и центробежного ускорений. Обозначается ускорение свободного падения буквой g и имеет различное значение для разных точек земного шара: от 9,78 м/с 2 (показатель для экватора) до 9,83 м/с 2 (значение ускорения на полюсах). На точность показателей влияют долгота, широта, время суток и некоторые другие факторы.

Для того чтобы продемонстрировать, как предмет падает в соответствии с открытием Галилея, ученые устраивают такой опыт: в длинную стеклянную трубку помещают предметы с различной массой, из трубки выкачивают воздух. После этого трубку переворачивают, все предметы под действием силы тяжести падают одновременно на дно трубки, независимо от их массы.

Когда эти же предметы помещены в какую-либо среду, одновременно с силой тяжести на них действует сила сопротивления, поэтому предметы в зависимости от своей массы, формы и плотности будут падать в разное время.

Формулы для расчетов

Существуют формулы, с помощью которых можно рассчитывать различные показатели, связанные со свободным падением. В них используются такие условные обозначения:

Формула для определения расстояния, пройденного падающим предметом при известной конечной скорости и времени падения: h = ut /2.

Формула для расчета расстояния, пройденного падающим предметом по постоянной величине g и времени: h = gt 2 /2.

Формула для расчета скорости предмета в конце падения, если известна высота, с которой падает исследуемый предмет: u = √2 gh.

Интересные факты

Если не углубляться в научные знания, бытовое определение свободного перемещения подразумевает передвижение какого-либо тела в земной атмосфере, когда на него не воздействуют никакие посторонние факторы, кроме сопротивления окружающего воздуха и силы тяжести.

В различное время добровольцы соревнуются между собой, пытаясь установить личный рекорд. В 1962 г. испытатель-парашютист из СССР Евгений Андреев установил рекорд, который был занесен в Книгу рекордов Гиннеса: при прыжке с парашютом в свободном падении он преодолел расстояние в 24500 м, во время прыжка не был использован тормозной парашют.

В 1960 г. американец Д. Киттингер совершил парашютный прыжок с высоты 31 тыс. м, но с использованием парашютно-тормозной установки.

В 2005 г. была зафиксирована рекордная скорость при свободном падении — 553 км/ч, а через семь лет установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.

Видео

Посмотрите интересное и познавательное видео, которое расскажет вам о скорости падения тел.

Источник

Закон падения тел

Ньютон, так же как и Галилей, начал исследования механического движения с изучения закона падения тел, но его задача была уже несколько проще. В распоряжении Ньютона имелся воздушный насос, о котором Галилей мог только мечтать.

Трубка Ньютона

Свои опыты Галилей проводил, бросая с Пизанской башни железные ядра, (подробнее: Галилей о свободном падении тел). Ньютон взял длинную стеклянную трубку, запаянную с одного конца, положил в нее маленький кусочек пробки и дробинку и присоединил трубку к воздушному насосу. Насос выкачал большую часть воздуха.

Ученый запаял второй конец трубки. И дробинка с кусочком пробки осталась в сильно разреженном воздушном пространстве. Ньютон поворачивал трубку то одним концом вверх, то другим — кусочек пробки и дробинка падали вниз с равной скоростью. Так удалось доказать, что в пустоте предметы разного веса падают с одинаковой скоростью. Теперь эти простенькие приборы — «трубки Ньютона» — имеются в каждой школе.

Скорость падения не зависит от веса

Скорость падения не зависит от веса. Падающие предметы веса не имеют, (подробнее: Вес падающего тела), говорил еще Галилей. Значит, сделал вывод Ньютон, вес — это не коренное свойство всех предметов или веществ. Весом любые предметы обладают лишь до тех пор, пока они на чем-либо лежат или висят, а когда падают — лишаются веса.

Что такое вес

Один из предшественников Ньютона — французский философ-математик Рене Декарт утверждал, что вес — это давление, которое оказывают вещи на землю или на подставку, на которой они лежат. Ньютон вспомнил опыты Галилея с ведрами. Пока вода переливалась из одного ведра в другое, их общий вес был меньше, чем раньше, — падающая вода двигалась свободно, ее ничто не задерживало, она действительно ничего не весила во время падения.

Как только вся вода оказывалась в нижнем ведре, равновесие весов восстанавливалось. И это тоже не удивляло Ньютона. Раз вся вода собралась в нижнем ведре, то и давление ее на дно должно в точности равняться сумме давлений воды в двух ведрах. Вода как бы снова обрела свой вес.

Почему тела давят на подставку

Но почему тела давят на подставку? Этого Декарт не знал. Возьмем гирю и подвесим ее на пружине. Пружина растянется. Теперь снимем эту гирю и возьмемся рукой за крючок пружины. Мы можем, приложив усилие, растянуть пружину настолько же, насколько ее растягивала своей тяжестью гиря. Тяжесть гири и сила руки оказывают на пружину одинаковое действие. Значит, причиной давления тел на подставку — их вес — является какая-то сила. Ее определил Ньютон.

Закон всемирного тяготения

Это земной шар притягивает к себе гирю и другие тела, удерживая их возле себя. Мы всюду и везде наблюдаем это явление и называем его тяготением. Изучением силы тяжести и ускорения свободного падения также занимался Галилей. Все тела, и большие и маленькие, притягиваются друг к другу, подчиняясь закону всемирного тяготения, открытому Ньютоном. Итак, вес — сила, с которой предметы, притягиваемые Землей, давят на удерживающие их подставки. Вес — проявление всемирного тяготения. Ньютон смог довести до логического завершения закон падения тел, которому положил начало Галилео ГалилеЙ.

Источник

Движение тела с ускорением свободного падения

теория по физике 🧲 кинематика

Свободное падение — это движение тела только под действием силы тяжести.

В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.

В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!

Ускорение свободного падения

Свободное падение

Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:

v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело

Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.

Подставляем данные в формулу и вычисляем:

Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.

Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.

Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.

Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:

Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:

Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.

Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:

Формула определения перемещения тела в n-ную секунду свободного падения:

s(n) — перемещение за секунду n.

Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.

Движение тела, брошенного вертикально вверх

Движение тела, брошенного вертикально вверх, описывается в два этапа

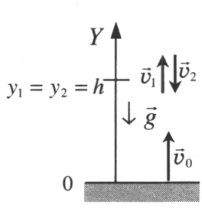
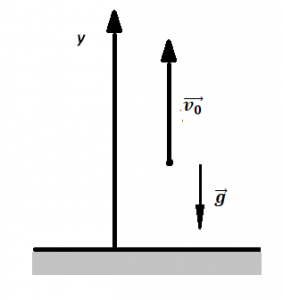
Два этапа движения тела, брошенного вертикально вверх Этап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v₀ и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях ( v ↑↓ g ). Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону ( v ↑↑ g ). Формулы для расчета параметров движения тела, брошенного вертикально вверх Перемещение тела, брошенного вертикально вверх, определяется по формуле:

Если известна скорость в момент времени t, для определения перемещения используется следующая формула:

Если время движения неизвестно, для определения перемещения используется следующая формула:

Формула определения скорости:

Какой знак выбрать — «+» или «–» — вам помогут правила:

Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h₂ > h₁). По этой же причине время второго этапов движения тоже будет больше (t₂ > t₁). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v₂ > v₀₁).

Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.

Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:

Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).

Уравнение координаты и скорости при свободном падении

Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:

Уравнение скорости при свободном падении:

Построение чертежа

Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.

Свободное падение на землю с некоторой высоты

Тело подбросили от земли и поймали на некоторой высоте

Уравнение скорости:

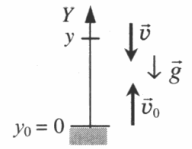
Тело подбросили от земли, на одной и той же высоте оно побывало дважды

Интервал времени между моментами прохождения высоты h:

Уравнение координаты для первого прохождения h:

Уравнение координаты для второго прохождения h:

Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.

Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Из условия задачи начальная скорость равна 0, а начальная координата — 50.

Через 3 с после падения тело окажется на высоте 5 м.

Алгоритм решения

Решение

Записываем исходные данные:

Перемещение (высота) свободно падающего тела, определяется по формуле:

В скалярном виде эта формула примет вид:

Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:

Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:

Вычисляем высоту, подставив известные данные:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу для определения скорости тела в векторном виде:

Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:

Подставим известные данные и вычислим скорость:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Скорость падения тел зависит от разности между плотностью падающего тела и плотностью среды.

0,6987241080194839238563680211997 Н – 0,6986499649689725185160051576173 Н = 0,000074143050511405340362863582 Н

0,0069872410801948392385636802119 Н – 0,0069864996496897251851600515761 Н = 0,000000741430505114053403628635 Н

Fg древесины ели на высоте 1 метра = 5,8246780481760035078688743363169 Н.

Fg древесины ели на высоте 100 метров = 0,058246780481760035078688743363169 Н.

Fg древесины ели на высоте 1 метра = 0,6986499649689725185160051576173 Н.

Fg древесины ели на высоте 100 метров = 0,006986499649689725185160051576173 Н.

с высоты 1 метра за 1,8362719084668811267057845545545545 с

с высоты 100 метров за 183,62719084668811267057845545545555 с.

с высоты 1 метра за 1,8363599913401219328180724941358 с

с высоты 100 метров за 183, 63599913401219328180724940556 с.

◄|| Закон гравитационного притяжения между двумя телами ||►

Источник

Предельная скорость падения

Согласно законам механики Ньютона, тело, находящееся в состоянии свободного падения, должно двигаться равноускоренно, поскольку на него действует ничем не уравновешенная сила земного притяжения. При падении тела в земной атмосфере (или любой другой газообразной или жидкой среде) мы, однако, наблюдаем иную картину, поскольку на сцену выходит еще одна сила. Падая, тело должно раздвигать собой молекулы воздуха, которые противодействуют этому, в результате чего начинает действовать сила аэродинамического сопротивления или вязкого торможения. Чем выше скорость падения, тем сильнее сопротивление. И, когда направленная вверх сила вязкого торможения сравнивается по величине с направленной вниз гравитационной силой, их равнодействующая становится равной нулю, и тело переходит из состояния ускоренного падения в состояние равномерного падения. Скорость такого равномерного падения называется предельной скоростью падения тела в среде.

Модуль предельной скорости падения зависит от аэродинамических или гидродинамических свойств тела, то есть, от степени его обтекаемости. В самом простом случае идеально обтекаемого тела вокруг него не образуется никаких дополнительных завихрений, препятствующих падению, — так называемых турбулентностей — и мы наблюдаем ламинарный поток. В ламинарном потоке сила сопротивления вязкой среды возрастает прямо пропорционально скорости тела. Вокруг мелких дождевых капель в воздухе, например, образуется классический ламинарный поток. При этом предельная скорость падения таких капель будет весьма мала — около 5 км/ч, что соответствует скорости прогулочного шага. Вот почему моросящий дождь порой кажется «зависшим» в воздухе. Еще меньшую предельную скорость имели масляные капли, использованные в опыте Милликена.

При движении в вязкой среде более крупных объектов, однако, начинают преобладать иные эффекты и закономерности. При достижении дождевыми каплями диаметра всего лишь в десятые доли миллиметра вокруг них начинают образовываться так называемые завихрения в результате срыва потока. Вы их, возможно, наблюдали весьма наглядно: когда машина осенью едет по дороге, засыпанной опавшей листвой, сухие листья не просто разметаются по сторонам от машины, но начинают кружиться в подобии вальса. Описываемые ими круги в точности повторяют линии вихрей фон Кармана, получивших свое название в честь инженера-физика венгерского происхождения Теодора фон Кармана (Theodore von Kármán, 1881–1963), который, эмигрировав в США и работая в Калифорнийском технологическом институте, стал одним из основоположников современной прикладной аэродинамики. Этими турбулентными вихрями обычно и обусловлено торможение — именно они вносят основной вклад в то, что машина или самолет, разогнавшись до определенной скорости, сталкиваются с резко возросшим сопротивлением воздуха и дальше ускоряться не в состоянии. Если вам доводилось на большой скорости разъезжаться на своем легковом автомобиле с тяжелым и быстрым встречным фургоном и машину начинало «водить» из стороны в сторону, знайте: вы попали в вихрь фон Кармана и познакомились с ним не понаслышке.

При свободном падении крупных тел в атмосфере завихрения начинаются практически сразу, и предельная скорость падения достигается очень быстро. Для парашютистов, например, предельная скорость составляет от 190 км/ч при максимальном сопротивлении воздуха, когда они падают плашмя, раскинув руки, до 240 км/ч при нырянии «рыбкой» или «солдатиком».

Источник