что вкладывают в понятие граф системы информатика
Графы
Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями (рёбрами), то мы получим информационную модель рассматриваемой системы в форме графа. Вершины графа могут изображаться кругами, овалами, точками, прямоугольниками и т. д.
Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер.
На рис. 1.6 с помощью взвешенного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.
Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью. Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
Графы как информационные модели находят широкое применение во многих сферах нашей жизни. Например, можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — рёбрами графа. По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.
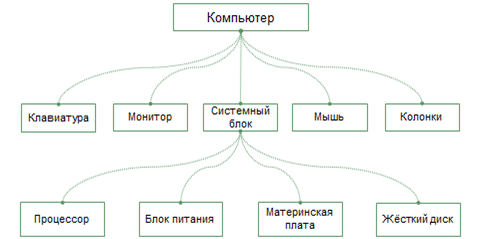
Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
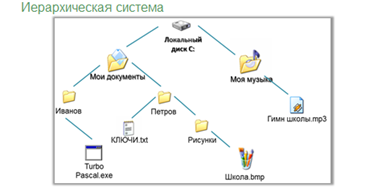
Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс 1 высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
1 Класс — множество объектов, обладающих общими признаками.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.

Теория Графов. Часть 1 Введение и классификация графов
«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена
Введение
Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.
Отмечу, что число вершин обозначается буквой n:
Число рёбер обозначается буквой m:
Таким образом граф задается и обозначается парой V,E:
Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)
Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.
Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.
Множество E задается парой неупорядоченных вершин множества V.
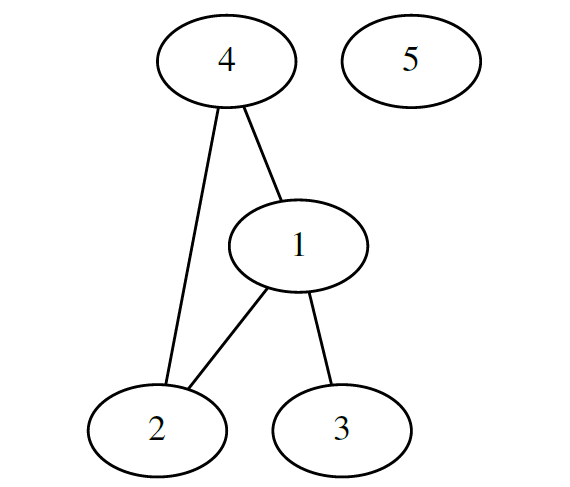
Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =
Граф будет выглядеть следующим образом:
Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.
Степень записывают, как:
Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:
Формула суммы степеней для G = V,E выглядит так:
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!
А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:
Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?
Классификации графов
Первым признаком классификации является отсутствие или наличие ориентации у ребер.
Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Вторым признаком является отсутствие или наличие кратных ребер.

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.
Заключение
В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.
Структурные модели систем. Графы
Урок 3. Информатика 11 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Структурные модели систем. Графы»
Вспомним ключевые термины прошлого урока.
Системный анализ – это исследование реальных объектов и явлений с точки зрения системного подхода, состоящее из этапов анализа и синтеза.
Модель «чёрного ящика» – это указание входов и выходов системы, а также зависимости между ними.
Модель состава – это своеобразный список элементов системы.
На данном уроке мы с вами узнаем, что такое структурная модель системы, что используется для её отображения, а также вспомним, из чего состоят графы.
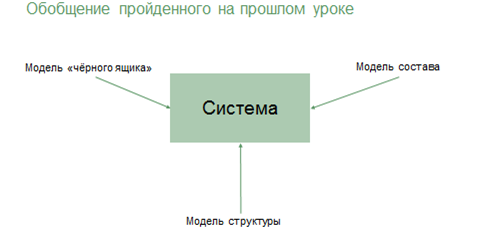
Если обобщить всё пройдённое на прошлом уроке, можно сказать, что модель «чёрного ящика», модель состава и модель структуры полностью описывают систему и образуют ещё одну модель, которая называется структурной моделью системы или структурной схемой. На структурной схеме отражается состав системы и её внутренние связи. Для отображения структурной схемы системы используются графы.
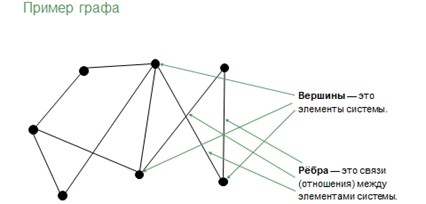
Граф – это совокупность объектов со связями между ними.
Графически это будет выглядеть следующим образом: вершины (точки) – это элементы системы, а ребра (линии между ними) – это связи (отношения) между элементами системы.
Примером графа является схема движения автобусов в городе, где вершины – это остановки, а рёбра – это пути передвижения автобусов. С помощью такой схемы проще определить на каком автобусе нужно доехать с одной остановки до другой.
Графы бывают ориентированными и неориентированными.
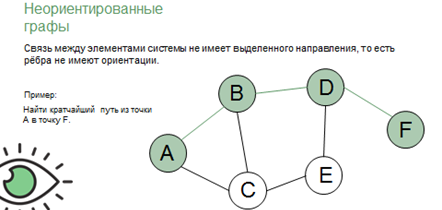
В неориентированных графах связь между элементами системы не имеет выделенного направления, то есть рёбра не имеют ориентации. Примером неориентированного графа будет являться решение задачи на нахождение кратчайшего пути. Граф для решения одной из таких задач, условием которой является нахождение кратчайшего пути из точки A в точку F, будет выглядеть следующим образом.
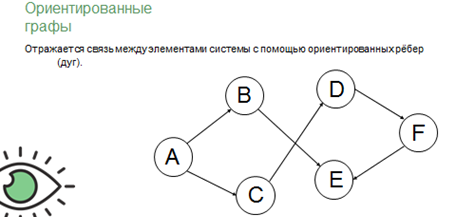
В ориентированных графах наоборот отражается связь между элементами системы с помощью ориентированных рёбер (стрелок). Такие рёбра называются дугами.
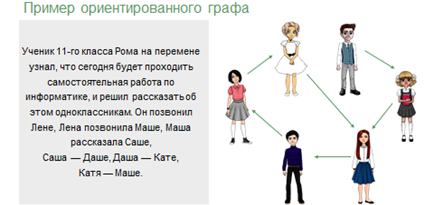
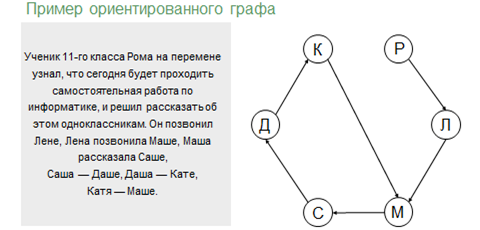
Так же с помощью дуг указывается не только наличие связи, но и какой из двух элементов является «началом» связи, а какой «концом». К примеру ориентированного графа можно отнести графическое изображение следующего условия: ученик 11 класса Рома на перемене узнал, что сегодня будет проходить самостоятельная работа по информатике, и решил рассказать об это одноклассникам. Он позвонил Лене, Лена позвонила Маше, Маша рассказала Саше, Саша – Даше, Даша – Кате, Катя – Маше.
Изобразим каждого учащегося как вершины графа, название которых будут отмечены первыми буквами имён, а звонки или разговоры дугами. Начало дуги будет находиться у вершины учащегося, который рассказывал про самостоятельную, а конец – у вершины того, кому рассказывали. Таким образом, мы получим ориентированный граф.
В ориентированном графе связями между вершинами будут дуги, а в неориентированном – рёбра.
Ещё графы бывают взвешенными. Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.
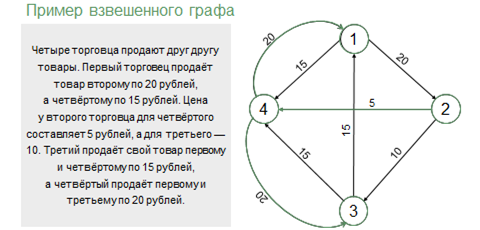
Нарисуем взвешенный граф на основе следующего условия: четыре торговца продают друг другу товары. Первый торговец продаёт товар второму по 20 рублей, а четвёртому по 15 рублей. Цена товара у второго торговца для четвёртого составляет 5 рублей, а для третьего – десять. Третий продаёт свой товар первому и четвёртому по 15 рублей, а четвёртый продаёт первому и третьему по 20 рублей. Для обозначения рыночных отношений между торговцами будем использовать дуги, а для указания веса, будем писать его над каждой дугой.
Для начала рисуем все вершины и обозначим их цифрами от одного до четырёх. Затем, по условию задачи первый торговец продаёт свой товар второму и четвёртому. Проведём стрелку от первого ко второму и от первого к четвёртому. Затем над каждой из них запишем соответствующую цену. Таким же образом оформляем весь граф. С помощью данного графа мы можем увидеть, что, например, для четвёртого торговца выгоднее продать товар первому и третьему, а купить у второго. И так далее.
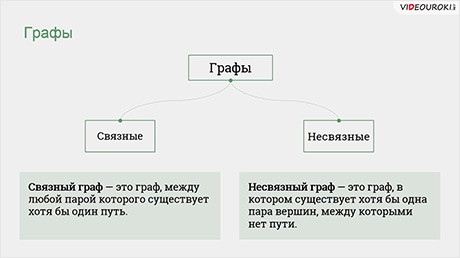
Так же графы бывают связными и несвязными.
Связный граф – это граф, между любой парой которого существует хотя бы один путь.
Примерами связных графов являются все вышерассмотренные графы.
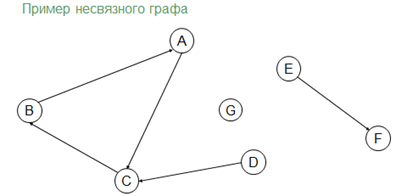
Несвязный граф – это граф, в котором существует хотя бы одна пара вершин, между которыми нет пути. Такие вершины называются несвязными. Например, на показанном графе несвязными вершинами является G и любая другая вершина данного графа.
Следующее понятие, с которым мы должны познакомиться: цепь. Итак, цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза. То есть, при построении пути, по одному и тому же ребру можно пройти только один раз.
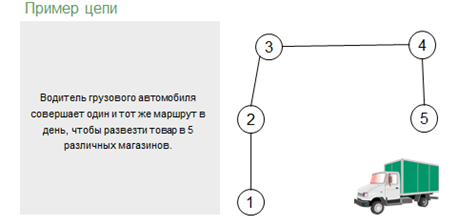
Например, водитель грузового автомобиля совершает один и тот же маршрут в день, чтобы развезти товар в пять различных магазинов. Давайте построим с помощью графа путь водителя. Обозначим вершинами все пять магазинов, и пронумеруем их от одного до пяти. Далее, водитель заехал в первый магазин, выгрузил необходимый товар и поехал во второй магазин. Изобразим ребром путь от первого магазина ко второму. Затем поехал в третий, четвёртый и пятый. Также изобразим данные пути с помощью рёбер. Обратите внимание, что водитель проезжает по каждому ребру только один раз. Данный граф будет являться примером цепи.
Цикл – это цепь, в которой начальная и конечная вершины совпадают.
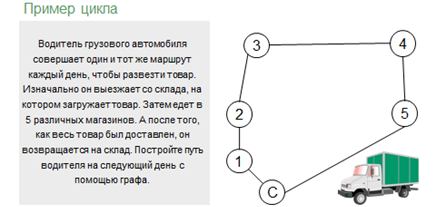
Разберём пример, похожий на предыдущий, но с некоторыми изменениями. Водитель грузового автомобиля совершает один и тот же маршрут каждый день, чтобы развезти товар. Изначально он выезжает со склада, на котором загружает товар. Затем едет в пять различных магазинов. А после того, как весь товар был доставлен, он возвращается на склад. Давайте снова построим путь водителя на следующий день с помощью графа. Обозначим вершинами склад и все пять магазинов, где цифры от одного до пяти будут обозначать магазины, а склад обозначим буквой «С». Изначально водитель заезжает на склад, затем едет в первый магазин, чтобы выгрузить необходимый товар. Обозначим этот путь ребром. Далее он едет из первого магазина во второй. Также изобразим ребром этот путь. Затем водитель едет в третий, четвёртый и пятый магазины. Снова изобразим данные пути с помощью рёбер. Из пятого магазина он едет на склад. Отметим этот путь на нашем графе. Обратите внимание, что водитель проезжает по каждому ребру только один раз и в конце возвращается в первоначальную вершину – на склад. Данный граф будет являться примером цикла.
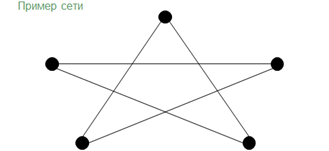
Сеть – это граф с циклом.
В качестве примера сюда можно отнести пятиконечную звезду, но прежде чем проводить ребра, обозначим точкой каждую из вершин. Затем начиная с нижней соединим их.
На практике часто приходится строить системы с иерархической системой. Такой граф называется деревом.
Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину. Отличительная особенность дерева: между любыми двумя его вершинами существует единственный путь.
Корень дерева – это единственная главная его вершина.
Каждая вершина дерева (кроме корня) имеет только одного предка. Обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков.
Потомки – это вершины, которые соответствуют классам нижнего уровня. Такой принцип связи называется «один-ко-многим».
Листья – это вершины, которые не имеют потомков.
Разберёмся более подробно на примере.
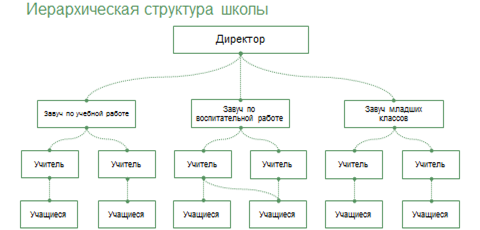
Давайте построим иерархическую структуру школы. Во главе будет находиться директор и соответственно он будет корневой вершиной нашего дерева. Далее на втором уровне будут находиться завуч по учебной работе, завуч по воспитательной работе, завуч младших классов, далее учителя и учащиеся. В данной структуре мы можем видеть, что Потомками являются все, кроме директора, предками – все, кроме учащихся, а листьями – учащиеся, так как в данной структуре у них нет потомков.
· Структурная модель системы отражает состав и внутренние связи системы.
· Граф – это графическое отображение структурной модели; состоит из вершин и линий (рёбер и дуг).
· Дерево – это ориентированный граф системы с иерархической структурой; связь – «один ко многим».
Графы: основы теории, алгоритмы поиска
Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.
Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.
Что такое граф?
Графы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.
С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.
В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.
Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:
Представление графов в коде
Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.
Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.
Матрицы смежности
Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.
Списки смежности
Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).
Поиск в глубину
Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).
Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.
Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:
Поиск в ширину
Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.
Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:
Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.
Заключение
Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.
Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!