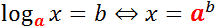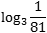что в математике значит лог

Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов

Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.

Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.

В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.

Итак, давайте разбираться, что такое логарифм.

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Основные свойства логарифмов

Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:

Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!

Рассмотрим свойства логарифмов на примерах.

Логарифмический ноль и логарифмическая единица

Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.

Запомните, что логарифм от a по основанию а всегда равен единице:

log_a a = 1 – это логарифмическая единица.

Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:

log_a 1 = 0 – логарифмический ноль.

Основное логарифмическое тождество

В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.

Вторая формула по сути является просто переформулированным определением логарифма

Разберем применение тождества на примере:

Необходимо найти значение выраженияСначала преобразуем логарифм

Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:

10 примеров логарифмов с решением

1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник

Логарифм (понятие).

Говоря другими словами логарифм числа b по основанию а формулируется как показатель степени, в которую надо возвести число a, чтобы получить число b (логарифм существует только у положительных чисел).

Из данной формулировки вытекает, что вычисление x= log_α b, равнозначно решению уравнения a x =b.

Достаточно часто используются вещественные логарифмы с основаниями 2 (двоичный), е число Эйлера e ≈ 2,718 (натуральный логарифм) и 10 (десятичный).

На данном этапе целесообразно рассмотреть образцы логарифмов log₇2, ln√5, lg0.0001.

А записи lg(-3), log_-33.2, log_-1-4.3 не имеют смысла, так как в первой из них под знаком логарифма помещено отрицательное число, во второй – отрицательное число в основании, а в третьей – и отрицательное число под знаком логарифма и единица в основании.

Условия определения логарифма.

Возьмем условие a≠1. Поскольку единица в любой степени равна единице, то равенство x=log_α b может существовать лишь при b=1, но при этом log₁ 1 будет любым действительным числом. Для исключения этой неоднозначности и берется a≠1.

Докажем необходимость условия a>0. При a=0 по формулировке логарифма может существовать только при b=0. И соответственно тогда log₀0 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0. А при a 0.

И последнее условие b>0 вытекает из неравенства a>0, поскольку x=log_α b, а значение степени с положительным основанием a всегда положительно.

Особенности логарифмов.

Логарифмы характеризуются отличительными особенностями, которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.

Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.

Источник

Что такое логарифм

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.

Мы же определим логарифм просто и наглядно. Для этого составим таблицу:

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Например, 2 3 = 8 ⇒ log₂ 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log₂ 64 = 6, поскольку 2 6 = 64.

Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log₂ 5 = 2,32192809.
log₃ 8 = 1,89278926.
log₅ 100 = 2,86135311.

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log₂ 5, log₃ 8, log₅ 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

Как считать логарифмы

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log _a x = b ⇒ x > 0, a > 0, a ≠ 1.

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log₁₀ x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log _e x

Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Источник

Что в математике значит лог

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

1. Поймете, что такое логарифм.

2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.

3. Научитесь вычислять простые логарифмы.

Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень.

Чувствую, сомневаетесь вы. Ну ладно, засекайте время! Поехали!

Для начала решите в уме вот такое уравнение:

3 x = 9

А теперь решите почти то же самое:

3 x = 8

Что, что-то не так? Ответ, что нету такого икса, не принимается!

Согласитесь, что это как-то нечестно – с девяткой пример решается в уме, а с восьмеркой не решается вовсе! Ну чем девятка лучше восьмерки?! Математика не терпит такой дискриминации. Для математики все числа равны! Ну, не буквально, конечно….

Можно сообразить, что икс – какое-то дробное число, между единичкой (3 1 = 3) и двойкой (3 2 = 9). И даже приближенно подобрать, найти это число. Но так возиться каждый раз. Математика решает вопрос как всегда радикально и элегантно. Просто введением понятия логарифма. Итак, что такое логарифм?

Вернёмся к нашему загадочному примеру:

3 x = 8.

Вот и назовём это число логарифмом восьми по основанию три. Записывается это вот как:

Читаем ещё раз: «икс равен логарифму восьми по основанию три».

И это правильный ответ!

Мы решили крутое показательное уравнение 3 x = 8!

И, неожиданно для себя, научились решать все показательные уравнения такого типа!

Это все верные ответы! Приятно, правда?

Представьте, мы в обыденной жизни спросили, например: «как доехать до вокзала?» И нам честно и правильно ответили: «На автобусе, который идёт до вокзала!» В жизни толку с такого ответа мало.

На вопрос: чему равен х в уравнении

Мы честно отвечаем: х равен числу, в которое надо возвести 3, чтобы получить 8! Или, чтобы так долго не говорить, пишем в сокращённом варианте, через логарифм:

Вас смущает, что вместо конкретного числа мы пишем какие-то значки с цифрами? Ну ладно, только для вас. Я покажу вам это конкретное число:

Легче стало? Учтите ещё, что это число никогда не кончается. Иррациональное оно.

Но радость от новых знаний будет неполной без ложки дегтя. Если логарифм считается без калькулятора, его надо считать. Ответ, например, х = log₂4 нехорош. Этот логарифм вычисляется, и его вы обязаны посчитать. Собственно, это и есть решение логарифма.

И чему же равен log₂4?

Да! В двойку надо возвести! Вот и ответ:

А log₃27 чему равен? Тройка в какой степени даст 27? В третьей! Ответ:

Уловили? Ну-ка разовьём успех! Решаем примеры:

Ответы (в беспорядке, разумеется!): 2; 1; 3; 4.

Что, тяжело сообразить, в какой степени шестёрка даст 216? А я предупреждал, что здесь таблицу умножения знать надо! Более того, намекну, что таблицу умножения вообще знать надо. Не только здесь.

Ну что, смотрим на часы? Сильно я ошибся?

До сих пор мы знали два жёстких ограничения. Нельзя делить на ноль и извлекать корень чётной степени из отрицательного числа. Эти ограничения играют огромную роль в решении заданий. Про ОДЗ помните? Теперь добавляются ограничения, связанные с логарифмами.

Запишем в общем виде, т.е. через буквы:

В результате получилось:

а > 0; a ≠ 1

А если мы положительное число возведём в любую степень, мы получим. получим. Да! Положительное число и получим. Отсюда:

Вот и все ограничения. Только на а и b. с может быть совершенно любым числом.

Ещё не мешает знать, что такое десятичный логарифм и что такое натуральный логарифм? В математике два основания употребляются очень часто. Это основание 10 и основание е. Число е.

Значки логарифмов по этим основаниям имеют своё написание.

Основание 10 не пишется, буква «о» пропадает. Такие логарифмы называются десятичными. И

Логарифмы по основанию «е» называются натуральными. Хотя чего уж там натурального.

Эти логарифмы ничем не отличаются от всех остальных! Ни по определению, ни по свойствам! Решение этих логарифмов ничем не отличается от решения обычных!

Пора переходить к лаконичным математическим формулировкам. К свойствам логарифмов. Популярное выражение «Решение логарифмов» предполагает не только вычисления, но и преобразования. По определённым правилам, естественно.

Запишем знакомое нам выражение:

Мы уже хорошо знаем, что если число а (основание) возвести в степень с, то получим число b. Это из самого определения логарифма следует. Стало быть, можно записать:

А теперь смотрим, чему же равно число с? Да вот оно:

Подставим это в предыдущую формулу, и получим:

И зачем нам эта перетасовка? Затем, что 4х-этажное выражение превращается в элементарное b! Это хорошее свойство!

Это первая формула свойств логарифмов. Её надо помнить! Единственная формула, где логарифм стоит в показателе степени.

Приведу ещё свойства, которые не требуют специальных выводов, а проистекают из определения логарифма и элементарной логики.

Чему равняется выражение:

В какую степень надо возвести а, чтобы получить 1? Неужто забыли? Нет? Ну, хорошо! Да, в нулевую! Вот и пишем:

Думаю, что следующее свойство уже не требует разъяснений:

Оставшиеся свойства логарифмов выводить не будем, я их приведу сразу в комплекте. Этот комплект надо знать! Это основа для решения логарифмов.

Свойства логарифмов.

здесь х>0, y>0, a>0, a≠1, m>0, m≠1.

Ещё отмечу, что эти формулы верны безо всяких оговорок для положительных х и у. В числовых логарифмах так обычно и бывает. А вот в уравнениях придётся модули использовать. Но там мы разберёмся со всеми подводными камнями, не волнуйтесь!

Ну, ладно. Формулы хорошие, решать-то как? Открываю тайну. Все задания на упрощение выражений с логарифмами решаются применением этих хороших формул (во, Америку открыл!). Попробуем, что-нибудь простенькое?

Надеюсь, всё понятно? Что, слишком элементарно? Ну ладно. Вот примеры чуток посложнее. Вычислить:

Ответы (в беспорядке): 2; 2,5; 4,5; 3.

Решилось? Неплохо! А ещё?

Тоже без проблем? Ну ладно. А вот это?

Ответы: 1; 36; 1; 2; 0,5.

Что, не всё решается? Или ничего не решается? Не переживайте, это дело поправимое. Вам прямая дорога в Раздел 555. Особый. Там подробно рассказано, как свойства логарифмов в дело употреблять. И не только для этих примеров, а и для всех сразу! Даны практические советы, которых вы не найдёте в учебниках. Очень рекомендую!

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник