что в геодезии принимают за математическую фигуру земли
Гранит и камень
Понятие о форме и поверхности Земли
Какова фигура у нашей планеты?
Знание фигуры и размеров Земли необходимо во многих областях и прежде всего для определения положения объектов на земной поверхности и правильного её изображения в виде карт, планов и цифровых моделей местности.
В настоящее время наиболее широкое использование получил геоцентрический эллипсоид WGS84 (World Goodetic System 1984). Он служит основой для измерения местоположений во всем мире. Система спутниковой навигации GPS сообщает координаты в системе эллипсоида WGS84 (World Goodetic System 1984).
Общеземной эллипсоид ориентируется в теле Земли согласно следующим условиям (определяемыми международными геодезическими организациями, которые организуются и направляются Международной ассоциацией геодезии, действующей по инициативе и в рамках Международного геодезического и геофизического союза):
Тем не менее, некоторые погрешности и отступления от реальной поверхности имеются при любых, применяемых в настоящее время, расчетах и измерениях.
Для геодезических работ рекомендуется использовать средний эллипсоид GRS80 (Geodetic Reference System 1980), принятый Генеральной Ассамблеей Международной ассоциацией геодезии в 1979 г.
Фигура геоида связана с направлением силы тяжести и, следовательно, существенно зависит от неравномерного распределения масс в земной коре. Поэтому поверхность геоида имеет неправильную, в геометрическом отношении весьма сложную фигуру с неравномерно изменяющейся кривизной. Однако исследованиями установлено, что поверхность геоида в общем близка к поверхности эллипсоида вращения с небольшим сжатием по направлению малой (полярной) оси.
Иногда такой эллипсоид называют сфероидом.
В геодезии для обозначения формы земной поверхности часто используют термин «фигура Земли».
Математическая поверхность Земли
1/300.
Постановлением Совета Министров СССР № 760 от 7 апреля 1946 года эллипсоид Красовского принят для территории нашей страны в качестве математической поверхности Земли.
В инженерной геодезии для практических расчетов за математическую поверхность Земли принимают шар со средним радиусом R = 6371.11 км. Объем шара равен объему земного эллипсоида.
Если на поверхности такого эллипсоида выделить фигуру в виде треугольника со сторонами примерно 25 км каждая, то окажется, что все линии в пределах поверхности этого треугольника, проложенные по поверхности эллипсоида, будут различаться по длине всего на 20 мм от длины прямых линий, соединяющих одноименные точки.
Такая разница для многих вычислений и измерений является настолько незначительной, что ей можно пренебречь и считать данные линии спроектированными не на сферическую поверхность, а на плоскость. Этим приемом пользуются при составлении планов и крупномасштабных карт.
Таким образом, участок сферической поверхности Земли в пределах треугольника со сторонами в 25 км (площадью до 320 кв. км) можно принять за плоскость.
При геодезических измерениях, не требующих повышенной точности, за плоскость условно принимается и окружность на поверхности Земли радиусом до 10 км.
Физическая поверхность Земли
Математические модели поверхности Земли, применяемые в геодезии



1. Если бы Земля была бы однородной, неподвижной и подвержена только действию внутренних сил тяготения, она имела бы форму шара(рис.1.2).
 |
2. Под действием центробежной силы, вызванной вращением вокруг оси с постоянной скоростью, Земля приобрела форму сфероида или эллипсоида вращения(рис.1.3).
 |
Рис. 1.3. Эллипсоид вращения
3. На самом деле, из-за неравномерного распределения масс внутри Земли, эллипсоидальная фигура Земли сдеформирована и имеет форму геоида (рис.1.4). Наибольшие отступления геоида от эллипсоида не превышают 100 – 150 м.
Т.о. специальными инструментами с физической поверхности Земли геодезические измерения проектируют на геоид, фигура которого не изучена. Фигуру геоида заменяют правильной математической фигурой, к которой можно применять математические законы. Размеры земного эллипсоида составляют:
большая полуось а = 6378245 м,
малая полуось b = 6356863 м,

4. Для того, чтобы земной эллипсоид ближе подходил к геоиду, его располагают в теле Земли, ориентируя определенным образом. Такой эллипсоид с определенными параметрами и определенным образом ориентированный в теле Земли, называется референц-эллипсоидом (рис.1.5).
 |
Рис. 1.5. Референц-эллипсоид
5. Геоид не может быть строго изучен из-за незнания распределения плотности масс внутри Земли. Было предложено вместо геоида принять фигуру квазигеоида (рис.1.6), которая может быть определена точно на основании астрономо-геодезических и гравиметрических измерений на поверхности Земли без учета внутреннего строения и плотности масс внутри Земли. Поверхность квазигеоидаотклоняется от поверхности геоида максимально 2 м в горных районах, на океанах и морях их поверхности совпадают.
Математическая поверхность Земли
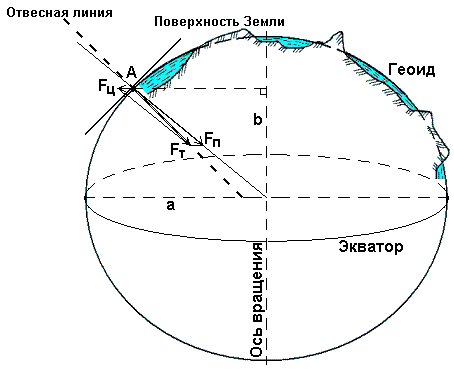
Рассмотрим любую материальную точку А на физической поверхности Земли (рис. 3).
На эту точку оказывают влияние две силы: сила притяжения Fп, направленная к центру Земли, и центробежная сила вращения Земли вокруг своей оси Fц, направленная от оси вращения по перпендикуляру. Равнодействующая этих сил называется силой тяжести Fт.
В любой точке земной поверхности направление силы тяжести, называемое ещё вертикальной или отвесной линией, можно легко и просто определить с помощью уровня или отвеса. Оно играет очень большую роль в геодезии. По направлению силы тяжести ориентируется одна из осей пространственной системы координат.
Если через точку А построить замкнутую поверхность, которая в каждой своей точке будет перпендикулярна отвесной линии (направлению силы тяжести), то данную поверхность можно принять в качестве математической при решении некоторых частных задач в геодезии. Такая поверхность получила название уровенной или горизонтальной. Её недостаток в том, что она содержит элемент неопределенности, т.е. через любую точку можно провести свою уровенную поверхность, и таких поверхностей будет бесчисленное множество.
Для устранения этой неопределенности при решении общих геодезических задач принимается так называемая общая математическая поверхность, т.е. уровенная поверхность, которая в каждой своей точке совпадает со средним уровнем морей и океанов в момент полного равновесия всей массы воды под влиянием силы тяжести. Такая поверхность носит название общей фигуры Земли или поверхности геоида.
Геоид – выпуклая замкнутая поверхность, совпадающая с поверхностью воды в морях и океанах в спокойном состоянии и перпендикулярная к направлению силы тяжести в любой её точке(см. рис. 3).
Из-за неравномерного распределения масс внутри Земли геоид не имеет правильной геометрической формы, и в математическом отношении его поверхность характеризуется слишком большой сложностью. Поэтому там, где это допустимо, поверхность геоида заменяется приближенными математическими моделями, в качестве которых принимается в одних случаях земной сфероид, в других – земной шар, а при топографическом изучении незначительных по размеру территорий – горизонтальная плоскость, т.е. плоскость, перпендикулярная к вертикальной линии в данной точке.
Земной сфероид – эллипсоид вращения получается вращением эллипса вокруг его малой оси b (см. рис. 3), совпадающей с осью вращения Земли, причем центр эллипсоида совмещается с центром Земли.
Размеры эллипсоида подбирают при условии наилучшего совпадения поверхности эллипсоида и геоида в целом (общеземной эллипсоид) или отдельных его частей (референц-эллипсоид).
Фигура референц-эллипсоида наилучшим образом подходит для территории отдельной страны или нескольких стран. Как правило, референц-эллипсоиды принимают для обработки геодезических измерений законодательно.
Наиболее удачная математическая модель Земли в виде референц-эллипсоида была предложена проф. Ф. Н. Красовским с большой полуосью a=6378245 м, малой – b=6356863м и коэффициентом сжатия у полюсов a = (a-b)/a = 1/298.3
Постановлением Совета Министров СССР № 760 от 7 апреля 1946 года эллипсоид Красовского принят для территории нашей страны в качестве математической поверхности Земли.
В инженерной геодезии для практических расчетов за математическую поверхность Земли принимают шар со средним радиусом R=6371.11 км. Объем шара равен объему земного эллипсоида.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Фигура Земли
100 метров, а на западе Тихого — поднята на
Фигура Земли — термин для обозначения формы земной поверхности. В зависимости от определения фигуры Земли устанавливаются различные системы координат.
Содержание
История вопроса
То, что форма Земли должна отличаться от шара впервые показал Ньютон. Он предложил следующий мысленный эксперимент. Нужно прокопать две шахты: от полюса до центра Земли и от экватора до центра Земли. Эти шахты заливаются водой. Если Земля имеет форму шара, то глубина шахт одинакова. Но на воду в экваториальной шахте действует центробежная сила, в то время как на воду в полярной шахте — нет. Поэтому для равновесия воды в обеих шахтах необходимо, чтобы экваториальная шахта была длиннее.
Современные представления о фигуре Земли
В нулевом приближении можно считать, что Земля имеет форму шара со средним радиусом 6371,3 км. Такое представление нашей планеты хорошо подходит для задач, точность вычислений в которых не превышает 0,5 %. В действительности Земля не является идеальной сферой. Из-за суточного вращения она сплюснута с полюсов; высоты материков различны; приливные деформации также искажают форму поверхности. В геодезии и космонавтике обычно для описания фигуры Земли выбирают эллипсоид вращения или геоид. С геоидом связана система астрономических координат, с эллипсоидом вращения — система геодезических координат.
По определению, геоид — это поверхность, всюду нормальная силе тяжести. [2] Если бы Земля целиком была бы покрыта океаном, то, в отсутствие приливного воздействия других небесных тел и прочих подобных возмущений, имела бы форму геоида. В действительности в различных местах поверхность Земли может значительно отличаться от геоида. Для лучшей аппроксимации поверхности вводят понятие референц-эллипсоида, который хорошо совпадает с геоидом только на каком-то участке поверхности. Референц-эллипсоиды в целом имеют геометрические параметры, отличные от геометрических параметров среднего земного эллипсоида, который описывает земную поверхность в целом.
На практике используется несколько различных средних земных эллипсоидов и связанных с ними систем земных координат.
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Понятие о фигуре Земли
Фигура Земли как планеты издавна интересовала ученых; для геодезистов же установление ее фигуры и размеров является одной из основных задач.
На вопрос: “Какую форму имеет Земля?” большинство людей отвечает: “Земля имеет форму шара!”. Действительно, если не считать гор и океанических впадин, то Землю в первом приближении можно считать шаром. Она вращается вокруг оси и согласно законам физики должна быть сплюснута у полюсов. Во втором приближении Землю принимают за эллипсоид вращения; в некоторых исследованиях ее считают трехосным эллипсоидом.
На поверхности Земли встречаются равнины, котловины, возвышенности и горы разной высоты; если же принять во внимание рельеф дна озер, морей и океанов, то можно сказать, что форма физической поверхности Земли очень сложная. Для ее изучения можно применить широко известный способ моделирования, с которым школьники знакомятся на уроках информатики.
При разработке модели какого-либо объекта или явления учитывают только его главные характеристики, имеющие значение для успешного решения данной конкретной задачи; все другие характеристики, как несущественные для данной задачи, во внимание не принимаются.
В модели шарообразной Земли поверхность Земли имеет сферическую форму; здесь важен лишь радиус сферы, а все остальное – морские впадины, горы, равнины, – несущественно. В этой модели используется геометрия сферы, теория которой сравнительно проста и очень хорошо разработана.
Модель эллипсоида вращения имеет две характеристики: размеры большой и малой полуосей. В этой модели используется геометрия эллипсоида вращения, которая намного сложнее геометрии сферы, хотя разработана также достаточно подробно.
Если участок поверхности Земли небольшой, то иногда оказывается возможным применить для этого участка модель плоской поверхности; в этой модели применяется геометрия плоскости, которая по сложности (а точнее, по простоте) несравнима с геометрией сферы, а тем более с геометрией эллипсоида.
В одном из учебников по высшей геодезии написано: “Понятие фигуры Земли неоднозначно и имеет различную трактовку в зависимости от использования получаемых данных”. При решении геодезических задач можно иногда считать поверхность участка Земли либо частью плоскости, либо частью сферы, либо частью поверхности эллипсоида вращения и т.д.
Какое направление вполне однозначно и очень просто можно определить в любой точке Земли без специальных приборов? Конечно же, направление силы тяжести; стоит подвесить на нить груз, и натянутая нить зафиксирует это направление. Именно это направление является в геодезии основным, так как оно существует объективно и легко и просто обнаруживается. Направления силы тяжести в разных точках Земли не параллельны, они радиальны, то-есть почти совпадают с направлениями радиусов Земли.
Поверхность, всюду перпендикулярная направлениям силы тяжести, называется уровенной поверхностью. Уровенные поверхности можно проводить на разных высотах; все они являются замкнутыми и почти параллельны одна другой.
Уровенная поверхность, совпадающая с невозмущенной поверхностью мирового океана и мысленно продолженная под материки, называется основной уровенной поверхностью или поверхностью геоида.
Если бы Земля была идеальным шаром и состояла из концентрических слоев различной плотности, имеющих постоянную плотность внутри каждого слоя, то все уровенные поверхности имели бы строго сферическую форму, а направления силы тяжести совпадали бы с радиусами сфер. В реальной Земле направления силы тяжести зависят от распределения масс различной плотности внутри Земли, поэтому поверхность геоида имеет сложную форму, не поддающуюся точному математическому описанию, и не может быть определена только из наземных измерений.
В настоящее время при изучении физической поверхности Земли роль вспомогательной поверхности выполняет поверхность квазигеоида, которая может быть точно определена относительно поверхно сти эллипсоида по результатам астрономических, геодезических и гравиметрических измерений. На территории морей и океанов поверхность квазигеоида совпадает с поверхностью геоида, а на суше она отклоняется от него в пределах двух метров /24/ (рис.1.1).
За действительную поверхность Земли принимают на суше ее физическую поверхность, на территории морей и океанов – их невозмущенную поверхность.
Что значит изучить действительную поверхность Земли? Это значит определить положение любой ее точки в принятой системе координат. В геодезии системы координат задают на поверхности эллипсоида вращения, потому что из простых математических поверхностей она ближе всего подходит к поверхности Земли; поверхность этого эллипсоида называется еще поверхностью относимости. Элли псоид вращения принятых размеров, определенным образом ориентированный в теле Земли, на поверхность которого относятся геодезические сети при их вычислении, называется референц-эллипсоидом.
Для территории нашей страны постановлением Совета Министров СССР N 760 от 7 апреля 1946 года принят эллипсоид Красовского:
большая полуось a = 6 378 245 м, малая полуось b = 6 356 863 м, полярное сжатие:
Применяемые в разных странах референц-эллипсоиды могут иметь неодинаковые размеры; существует и общеземной эллипсоид, размеры которого утверждают Международные геодезические организации. Так, в системе WGS-84 (World Geodetic System) эти размеры суть большая полуось a = 6 378 137.0 м, полярное сжатие:
Малая полуось при необходимости вычисляется через a и α.
Для многих задач геодезии поверхностью относимости может служить сфера, которая в математическом отношении еще проще, чем поверхность эллипсоида вращения, а для некоторых задач небольшой участок сферы или эллипсоида можно считать плоским.