что быстрее скорость звука или скорость звука быстрее
Скорость звука и число М
Для начала давайте выясним, сверхзвук — это сколько км/ч? Какова должна быть скорость, чтобы считаться сверхзвуковой? Проблема в том, что простого и однозначного ответа на этот вопрос… Просто нет.
Есть правильный ответ — больше 1 М. Или Число Маха равное единице, это скорость звука, а выше единицы, это уже сверхзвук.
Совсем не привычное нам число, выраженное в километрах в час. Если упростить, то объяснить можно так: скорость звука зависит о свойств среды в которой он распространяется, чем плотнее среда, тем быстрее распространяются колебания (звук это ведь волна). Таким образом на разной высоте скорость звука разная. Чем выше, тем меньше плотность воздуха и тем ниже будет местная скорость звука.
Что такое скорость звука
Скорость звука в километрах в час не выражается, просто потому, что в таком случае она всегда будет разной.
Зависимость скорости звука от высоты полета
Например, скорость звука у земли (на высоте 0 км) составит 340 метров в секунду (м/с), это 1224 км/ч. И тут важно сказать что такое значение будет: при температуре +15 и давлении 750 мм. рт. ст. и относительной влажности 0%. То есть, при «стандартных» условиях.
А вот на высоте 10 000 метров, на которой летают современные пассажирские лайнеры, это уже около 299 м/с (это 1076 км/ч), то есть разница довольно значительная — 12%.
Также от высоты полета и других параметров атмосферы зависит и скорость звука, и сопротивление воздуха и, соответственно, скорость самолета, которую он может развить.
Скорость звука на высоте 11 километров и выше почти не будет меняться, эта часть атмосферы называется «тропопауза».
То же самое в виде таблицы
Зависимость скорости звука от высоты*
| Высота, м | Скорость звука, м/с | Скорость звука, км/ч |
| -1000 | 344,1 | 1 238,8 |
| 0 | 340,3 | 1 225,1 |
| 1000 | 336,4 | 1 211,0 |
| 2000 | 332,5 | 1 197,0 |
| 3000 | 328,6 | 1 183,0 |
| 4000 | 324,6 | 1 168,6 |
| 5000 | 320,6 | 1 154,2 |
| 6000 | 316,5 | 1 139,4 |
| 7000 | 312,3 | 1 124,3 |
| 8000 | 308,1 | 1 109,2 |
| 9000 | 303,9 | 1 094,0 |
| 10000 | 299,6 | 1 078,6 |
| 11000 | 295,2 | 1 062,7 |
| 12000 | 295,1 | 1 062,4 |
| 13000 | 295,1 | 1 062,4 |
| 14000 | 295,1 | 1 062,4 |
*Минутка занудства. Нужно напомнить, что на самом деле скорости звука от высоты зависит условно, это упрощение. Скорость звука зависит от плотности атмосферы, а плотность воздуха, в свою очередь, зависит от температуры, влажности и давления, которые меняются с высотой.
Зачем нужно число Маха
Так вот, число Маха в авиации представляет собой отношение скорости летательного аппарата к скорости звука на той высоте на которой он сейчас летит. Так удобнее, ведь на разной высоте скорость звука будет разной и чтобы понимать достигает ли самолет скорости звука, его скорость измеряют в числах М.
Один мах, это просто — 1 мах, а не «км/ч». Нельзя просто ответить на вопрос «сколько 1 мах в километрах в час», нужно всегда уточнять, о какой высоте идет речь.
Если еще проще, число М показывает сколько скоростей звука в скорости самолета сейчас на конкретной высоте (при определенных условиях среды). Если число Маха больше единицы, очевидно, мы имеем дело со сверхзвуковой скоростью. Поэтому чаще всего вы будете встречать пояснение для какой высоты указано конкретное число Маха.
Например, для Боинга 777 крейсерской скоростью считается 0,84 М (это дозвуковой летательный аппарат). То есть на высоте 10 000 метров при стандартных условиях, принимая скорость звука за 1076 км/ч умножаем ее на 0,84 и получаем — 904 км/ч. По документации крейсерская скорость Boeing 777 составляет как раз 905 км/ч.
Что касается сверхзвуковых летательных аппаратов, то, по определению, их скорости должны быть больше скорости звука, то есть больше 1 М. Например у Су-27 это 2,35 М, что примерно 2 528 км/ч на высоте 10 км (скорость звука 295 м/с, а это 1062 км/ч).
Число М некоторых сверхзвуковых самолетов:
А вот гиперзвуковые летательные аппараты:
SR-71 — самый быстрый серийный самолет
Еще одно замечание, число Маха в авиации, это качественная величина, а не количественная. То есть это не скорость в чистом виде, а критерий который показывает насколько скорость объекта выше скорости звука. Зачем? Затем, что дозвуковые, трансзвуковые, сверхзвуковые или гиперзвуковые скорости очень сильно отличаются по сути.
Пилоту (и инженеру тоже) важно знать какой у него сейчас режим обтекания самолета (дозвуковой, трансзвуковой или сверхзвуковой). Например, во многих указателях скорости есть отдельный циферблат, показывающий значение числа Маха в дополнению к приборной скорости.
На картинке в начале этого повествования изображен трансзвуковой режим. Это значит, что сам самолет еще не превысил скорость звука, а на некоторых его участках (на фото это очень хорошо видно по белым «клиньям») скорость обтекания уже достигла скорости звука.
Поэтому и образовались скачки уплотнения которые хорошо видны благодаря образованию конденсата позади них. Вот почему, число Маха так важно.
Что быстрее всего на свете — звук или свет?
Человек за час неспешной ходьбы преодолевает 4 км. Скорость ветра — 35-70 км/ч, космической ракеты — 8 км/с. Земля, вращаясь вокруг Солнца, только за одну секунду проходит 30 км. Быстрым движением считается то, которое мы перестаем улавливать на близком расстоянии. Пример: летящие пули, снаряды. Но что быстрее всего на свете? Статья будет ответом на этот вопрос.
Как измеряли скорость света
Людей всегда интересовало, что быстрее всего на свете. Многие ученые пытались выяснить, распространяется ли свет мгновенно или с задержкой, но сделать это впервые удалось датчанину О. Ремеру. В 1676 г астроном наблюдал за движением спутника Юпитера и заметил, что он периодически опаздывает. То, что расстояние между Землей и и этим газовым гигантом меняется, было закономерно: в момент каждого нового наблюдения наша планета смещалась по орбите.

Как измеряли скорость звука
Через 50 лет Исаак Ньютон рассчитал скорость звуковой волны. Оказалось, что его теоретический результат и результат эксперимента Мерсенна очень сильно отличаются. Лишь в 1808 г француз Пуассон пришел к выводу, что величина, полученная Ньютоном, верна только для постоянной температуры воздуха, чего в обычных условиях добиться невозможно.
В 1822 г опыты группы французских ученых подтвердили догадки. Вывод был таков: скорость звука зависит от температуры, чем она выше, тем быстрее распространяется звуковая волна.
Звук или свет — что быстрее?
При нулевой температуре воздуха скорость звука составляет 331 м/с. При 20° С — 344 м/с. Звуковая волна распространяется не только в воздухе, но и в жидкостях, твердых телах. Известно, что чем больше вещество сопротивляется сжатию, тем лучше проводит звук. Так, скорость звука в воде — 1484 м/с. Металлы, например, алюминий, сталь, железо, проводят звук со скоростью 5000-6000 м/с, а сапфир — со скоростью 11400 м/с.
Полученная Ремером величина скорости света слегка корректировалась, и не раз, потому что со временем менялись методы измерений, расчетов. Свет проходит расстояние в 150 млн км за 8 минут. Его скорость немного меньше 300 тыс. км/с, но для удобства вычислений величину принято округлять.
Сегодня науке доподлинно известно: свет — это то, что быстрее всего на свете. Иными словами, эти частицы двигаются быстрее всех.
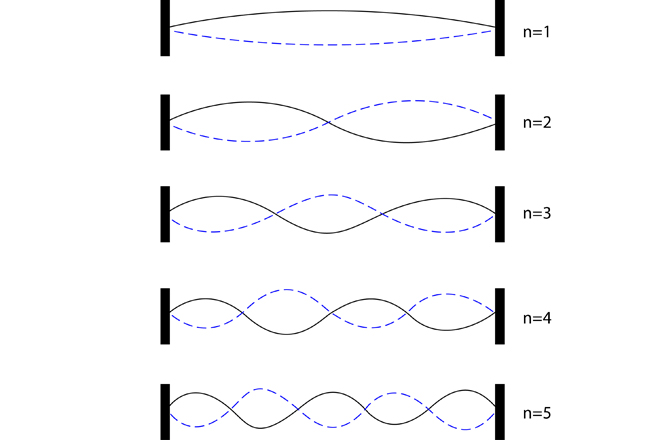
Звуковые волны
Звуковые волны или звук – это колебания частиц, распространяемые волнообразно в какой-либо среде – газообразной, жидкой или твёрдой, – которые воспринимаются органами слуха животных.
Когда мы изучаем свет, то убеждаемся не только в том, что он существует вне нас, но сверх того еще и в том, что нам необходимо иметь глаза для восприятия света, иначе мы и не подозревали бы о нем. Всё вокруг нас погружается в темноту, когда мы закрываем глаза. Точно так же для нас не существовало бы мира звуков, если бы у нас не было органа слуха, который воспринимает их.
Итак, мы называем звуком то, что мы чувствуем нашим слуховым аппаратом. Но явления внешнего мира для нас имеют характер звуковых только с того момента, когда они дошли до наших ушей. Закрыв уши пальцами, мы не услышим разговора, хотя он и продолжается около нас.
Из этого следует, что как бы ни были грандиозны звуковые явления, происходящие на Солнце и Луне, они не могут произвести такого шума, который мог бы быть услышан у нас на Земле, потому что за пределами нашей атмосферы, между Землей и небесными телами, нет обычной материи.
Источники звуковых волн
Мы говорим, что звук есть волнообразные движения или колебания. Каждый, кто видел или чувствовал то, что происходит, когда рождается звук, тотчас согласится с этим. Так, например, если крепко натянуть нить и потом быстро ударить по ней, то можно видеть, как она заколеблется. И услышать при этом небольшой музыкальный звук. То же самое будет наблюдаться в звучащей фортепианной струне или в колоколе. И мы можем ощущать эти колебания, если дотронемся до них.
Мы также знаем, что при ударе по стеклу оно издает звук, который прекращается, если прикосновением пальца прекратить его колебания. Все эти явления служат доказательством того, что известные колебания производят звук. Каждый раз, когда колеблется колокольчик, стакан или струна, воздух получает от них легкие удары. В нем образуется ряд волн, доходящих до нашего уха, вот почему мы и слышим звук.
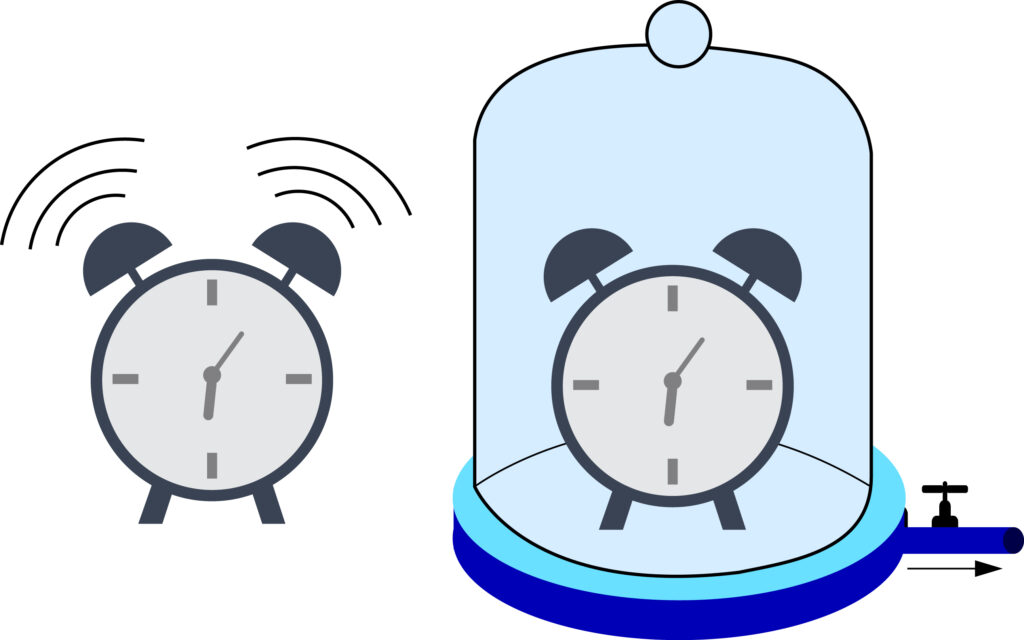
Нетрудно доказать, что воздух проводит звуковые волны. Для этой цели производят следующий опыт: под стеклянный колпак воздушного насоса помещают электрический звонок, заставляют его непрерывно звенеть. Затем начинают насосом выкачивать воздух.
Когда уменьшается количество воздуха под колпаком, мы видим звонок так же хорошо, как и раньше, потому что свет распространяется, когда воздуха нет. Но звук делается все тише и наконец совершению прекращается. Колебания звонка продолжают совершаться, но так как вокруг него больше нет воздуха, то он не может производить те волны. которые мы называем звуковыми. Если же воздух начинает снова входить под колпак, то звук восстанавливается. Этот простой опыт показывает нам не только то, что воздух служит проводником звука, но и то, что сила звука в значительной степени зависит от состояния воздуха.
Когда у нас появляется возможность сравнить скорость света со скоростью звука, то мы находим между ними огромное различие. Но видим огонь и дым при стрельбе из отдаленной пушки на несколько секунд раньше звука от ее выстрела. Свет распространяется так быстро, что даже значительное расстояние, на котором находится от нас действующее орудие, он проходит в какую-нибудь тысячную долю секунды; тогда как звук распространяется гораздо медленнее, и скорость его распространения при таком опыте очень легко вычислить.
Распространение звуковых волн
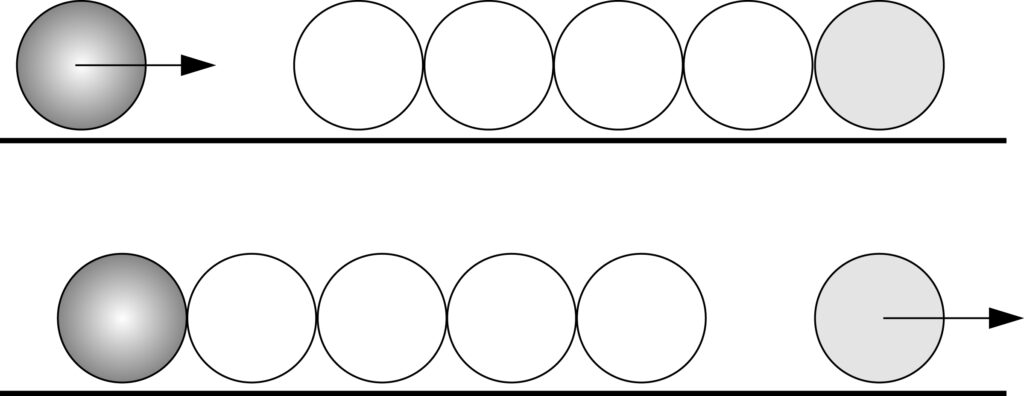
Возьмем несколько бильярдных шаров и положим их прямой линией на бильярдном столе так, чтобы они касались друг друга. Затем возьмем еще шар и покатим его так, чтобы он ударил в шар, лежащий на конце ряда. Тогда каждый из шаров в ряду будет попеременно сжиматься и производить давление на следующий за ним, в результате чего шар, находящийся на другом конце ряда, отскочит от него.
Каждый шар ряда здесь попеременно сжимается и расширяется. То же самое случается и в воздухе, когда звук проходит через него. Мы можем представить себе, что волну принуждают двигаться частицы воздуха, ударяющие одна о другую при своих движениях взад и вперед, точно так, как эти бильярдные шары.
Скорость звука
Скорость света одинакова при всех условиях, насколько это можно было изучить. А скорость звука изменяется в значительной степени с изменением условий, при которых он распространяется в воздухе. Большое счастье для музыкального искусства заключается в том, что скорость звука изменяется только в незначительной степени с изменением высоты его или силы.
Было бы очень затруднительно слушать издали музыку, если бы звуки различных инструментов оркестра доходили до нашего слуха в разное время, в то время как композитор имел в виду, что они будут слышаться одновременно. Или, если бы мотив, разыгрываемый одной частью оркестра, доходил до нашего слуха раньше того, что играет другая часть оркестра, или позже.
1. Скорость звука в воздухе
Обычная скорость звука в воздухе считается около 331 метра (То есть около трети километра) в секунду. Когда температура воздуха поднимается, он становится более упругим и тогда прохождение звука через него совершается быстрее.
Скорость звука увеличивается с повышением температуры воздуха, если плотность его остается той же самой.
Если мы примем во внимание зависимость скорости звука от упругости проводящей его среды, то нам будет понятно, почему звук проходит значительно быстрее в жидкостях, чем в газах, и еще быстрее в твердых телах.
2. Скорость звуковых волн в твёрдых телах
Звуковые волны распространяются в твёрдых телах быстрее, чем в воздухе. Железо, когда оно в твердом состоянии, обладает большею упругостью, чем воздух, и звук проходит в нем почти в семнадцать раз быстрее, чем в воздухе
Нельзя смешивать скорость распространения звука в воздухе или в какой-либо другой среде с высотой тона. Она у музыкального звука зависит от числа колебаний в секунду, и чем их больше, тем выше тон.
Звук, как мы сказали, проходя через железо, достигает нашего уха в семнадцать раз быстрее, чем когда он проходит через воздух; высота же его тона остается той же самой в обоих случаях, потому что число колебаний в секунду остается одно и то же, хотя звук через железо проходит значительно быстрее.
3. Скорость звука в разных средах
Сила звука
Когда мы начнем исследовать силу звука на разных расстояниях, то найдем, что первый закон, относительно его, тот же, что и для света. И насколько нам известно, этот закон верен не только относительно волнообразных движений, но и такого явления, как тяготение.
На точном научном языке закон о силе звука излагается так:
Сила звука изменяется обратно пропорционально квадрату расстояния от его источника
Таким образом можно коротко и ясно выразить, например, ту мысль, что если мы удаляемся от источника звука на расстояние, которое в три раза больше прежнего, то сила звука уменьшится при этом не в три, а в девять раз: девять есть квадрат трех. Квадратом числа называется число, полученное от перемножения его на самого себя.
Когда этот закон применяется к силе света или тяготения, то нам не приходится считаться с какими-либо условиями, которые могут повлиять на них. Но если речь идёт о звуке, то дело обстоит несколько иначе. На звук влияет плотность той среды, в которой он проходит; в морозную ночь воздух очень плотен, почему нам и дышится тогда легче, звук же будет в это время слышен сильнее. С другой стороны, звук ружейного выстрела высоко в горах ослабляется, потому что воздух там редок. Это явление напоминает нам опыт со звонком под колпаком воздушного насоса.
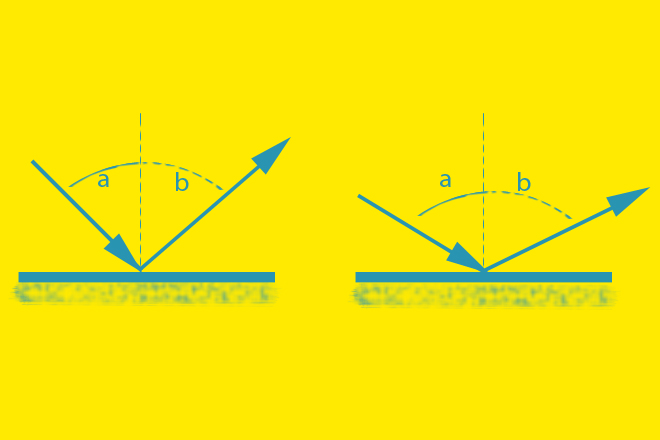
Отражение звука
Когда мы наблюдаем, как волны моря или озера ударяют в крутой берег, мы видим, что они отражаются от него и отскакивают назад. Если поверхность берега ровная и вертикальная, то мы видим, что волны отражаются от нее точно так же, как мяч от стены. Если звук есть действительно волнообразное движение, то мы всегда можем ожидать, что и он будет так же отражаться, как водяные волны, и нам часто приходится убеждаться в этом.
Всякие движущиеся волны могут отражаться от преград на их пути; это совершается как при свете, так и при морских волнах. Есть законы отражения, которые одинаково приложимы к этим различным явлениям.
Природа грома
Мы все хорошо знаем, что на открытом воздухе звук кажется нам не таким, как в закрытом помещении. И наш голос в разных местах звучит различно. Все эти явления зависят от особенностей отражения звука в разных местах.
Самым лучшим способом для доказательства отражения звука может служить эхо. Мы можем довольно простым способом определить скорость звука, стоит только нам произвести звук на некотором расстоянии от отражающей его поверхности и заметить, как быстро мы услышим эхо.
Лучшим примером отражения звука, производящего эхо, являются раскаты грома, случающиеся во время грозы:
Волны Рэлея
Если мы наполним резиновый шар или выпуклый диск углекислым газом, то заметим, что он действует на звук точно так, как зажигательное стекло на световые лучи. Звуковые волны отклоняются газом, находящимся в шаре, так что они все собираются в одном пункте, находящемся по другую сторону шара точно так, как лучи солнца могут быть собраны на кусок бумаги в одну точку зажигательным стеклом.
Это видно из хорошо известного опыта, произведенного замечательным английским ученым, лордом Рэлеем. Опыт этот заключается в том, что нас ставят против часов на таком расстоянии, чтобы не слышать их тиканья. Если после этого гуттаперчевый шар, наполненный углекислым газом, будет помещен между нами и часами, то, находясь на том же самом расстоянии, мы услышим часы. Это происходит вследствие того, что углекислый газ преломляет звуковые волны и фокусирует их в одной точке.
Скорость звука: каков ее предел?
Одна из основных задач какой-либо точной науки заключается в измерении и объяснении тех или иных процессов, а также их участников. За многие годы исследований, расчетов и споров научное сообщество пришло к пониманию того, что существуют определенные ограничения в некоторых явлениях. К примеру, скорость света в вакууме равна 299 792 458 м/с. Согласно специальной теории относительности, ничто не может двигаться быстрее. Другими словами, мы имеем верхний скоростной лимит для света. Однако такой лимит для скорости звука пока не был установлен. Ученые из Лондонского университета королевы Марии (Англия, Великобритания) провели расчеты, результатом которых стало открытие верхнего предела скорости звука. Что стало основой расчетов, каковы их результаты, и в каких областях можно применить новообретенные знания? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.
Основа исследования
Звук это волны механических колебаний в какой-либо среде. Скорость распространения этих волн напрямую зависит от самой среды. К примеру, в твердых объектах звук распространяется быстрее, чем в воздухе. Однако и тут могут быть флуктуации в измерениях, поскольку важна не только среда как таковая, но и ее состояние (температура, давление и т.д.).
Логично, что скорость звука сложно назвать константой, так как в разных условиях она будет своя: в воздухе это 331 м/с, в воде 1500 м/с (тут будут вариации в зависимости от температуры, давления и солености воды), а в стекле 4800 м/с.
Но как же рассчитать верхний лимит скорости звука?
Как напоминают нам ученые, некоторые важные свойства конденсированных фаз* определяются фундаментальными физическими константами.
Конденсированные фазы* — состояние вещества, когда число его компонентов (атомов, молекул и т.д.) крайне велико, а взаимодействия между компонентами очень сильны. К числу таких фаз можно отнести и твердые вещества, и жидкости.
Постоянная Ридберга* — предельное значение наивысшего волнового числа любого фотона, который может быть испущен атомом водорода. Также эта постоянная определяет волновое число фотона с наименьшей энергией, способного ионизировать атом водорода в его основном состоянии.
Постоянная тонкой структуры* (⍺) — фундаментальная физическая постоянная, которая характеризует силу электромагнитного взаимодействия. Эта постоянная определяет размер крайне малого изменения величины энергетических уровней атома и образования тонкой структуры, которые являются набором узких и близких частот в его спектральных линиях.
Отношение массы протона к массе электрона* (mp/me — константа, равная 1836,15267261.
Объединение этих констант позволяет определить новую безразмерную константу, описывающую верхнюю границу скорости звука (vu) в конденсированных фазах (формула №1): 
где c — скорость света в вакууме, ⍺ — постоянная тонкой структуры, mp/me — отношение масс протона и электрона, vu — верхний предел скорости звука.
Подтверждение верности данной формулы было получено благодаря многочисленным экспериментам и моделированию атомарного водорода.
Результаты исследования
Авторы сего труда отмечают, что существует два подхода к определению v (скорости звука). Один поход начинается с оценки упругости системы, а второй — с оценки ее вибрационных свойств. Оба подхода дают сопоставимые результаты (приготовьтесь, формул будет немало).
Используя E = ER из формулы №3 в формуле №2 мы получим (формула №4): 
где ⍺ = (1/4πϵ0)(e 2 /hc) — постоянная тонкой структуры.
Такой же результат, как и в формуле №4, можно получить и посредством второго подхода, где основной акцент поставлен на рассмотрении вибрационных свойств системы.
Далее выбранный подход был проверен на более практическом уровне.
me характеризует электроны, которые отвечают за взаимодействия между атомами. Электронный вклад далее отражается в коэффициенте ⍺c (⍺c ∝ e 2 /h), который представляет собой скорость электронов в модели Бора. Ученые отмечают, что ⍺с и v не зависят от c. Использование формулировки v в виде ⍺с в формуле №4 обусловлено двумя факторами.
Во-первых, так намного удобнее и информативнее представлять границу в отношении vu/c, что обычно применяется в отношении скорости Ферми и скорости света (vF/c).
Во-вторых, именно ⍺ (наряду с mp/me) имеет фундаментальное для стабильности протонов и обеспечения синтеза тяжелых элементов и, следовательно, существования твердых тел и жидкостей, в которых звук может распространяться.
m формула №4 характеризует атомы, участвующие в распространении звука. Его масштаб задается массой протона mp: m = Amp, где A — атомная масса. Учитывая, что А = 1, а m = mp, применение формулы №4 позволяет определить значение верхней границы скорости звука (формула №9): 
Таким образом было показано, что vu зависит только от фундаментальных физических констант, включая безразмерную постоянную тонкой структуры и отношение масс протона и электрона.
Вышеуказанная формула является расширенным вариантом формулы №4 для атомарного водорода. Объединение формул №4 и №9, при учете m = Amp, позволяет получить (формула №10): 
Что ж, теперь можно немного отдохнуть от формул и приступить к обсуждению расчетов и экспериментов.
Ученые отмечают, что хоть скорость звука определяется модулями упругости и плотностью, они существенно отличаются в зависимости от типа связи: сильные ковалентная, ионная или металлическая связи, обычно дающей большую энергию связи, промежуточные водородные связи, а также слабые дипольные и ван-дер-ваальсовые взаимодействиям. Модули упругости и плотность также меняются в зависимости от конкретной конструкции, которую принимает система. Кроме того, тип связи и структура сами по себе взаимозависимы: ковалентная связь приводят к образованию открытых структур, а ионная — плотноупакованных. Следовательно, скорость звука для конкретной системы не может быть предсказана аналитически и без явного знания структуры и взаимодействий внутри нее, подобно другим системно-зависимым свойствам, таким как вязкость или теплопроводность.
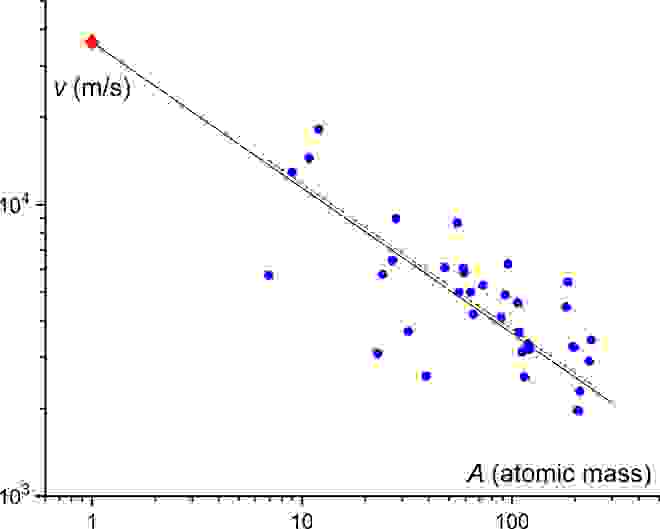
Тем не менее зависимость v от m или A может быть изучена в семействе элементарных твердых тел. Элементарные твердые вещества не имеют смешанных особенностей, существующих в соединениях из-за смешанной связи между разными атомными разновидностями (включая смешанную ковалентно-ионную связь между одними и теми же парами атомов, а также разные типы связи между разными парами).
Изображение №1
Коэффициент корреляции Пирсона* используется для изучения связи двух переменных, измеренных в метрических шкалах на одной и той же выборке.
Расчетные и экспериментальные значения vu, показанные на графике прямой и пунктирной линиями, указывают на пересечение в точке 37.350 м/с, что подтверждает верность расчетных походов и, особенно, верность аппроксимации коэффициент в формуле №4, что дает хорошее согласование с экспериментальными данными.
Изображение №2
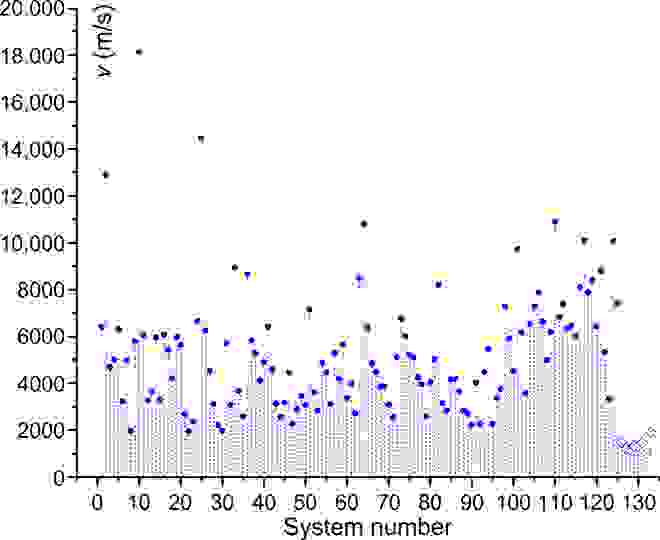
Далее было решено проверить согласование расчетных данных с экспериментальными с применением более широкого спектра образцов (133 образца). Экспериментальные значения v были меньше, чем верхняя теоретическая граница vu в формуле №9. vu примерно вдвое больше v в алмазе, это является самой высокой скоростью звука, измеренной в условиях окружающей среды.
Формула №10 может использоваться для приблизительного прогнозирования средней или характеристической скорости звука (v). A1/2, которая, согласно формуле №10, относится к скорости звука, варьируется по периодической таблице в диапазоне от 1 до 15 со средним значением 8. Согласно расчетам соответствующее значение v равно 4513 м/с. Это на 16% согласуется с 5392 м/с — средним значением по всем элементарным твердым телам, и на 14% с 5267 м/с — средним значением по всем твердым телам на графике выше.
В эксперименты также были включены данные по скорости звука в жидкости при комнатной температуре, которые варьируются от 1000 до 2000 м/с. Однако в высокотемпературных жидких металлах, таких как Al, Fe, Mg и Ni, v достигает более высоких значений в диапазоне от 4000 до 5000 м/с. Из этого следует, что скорость звука в жидкостях полностью удовлетворяет расчетную верхнюю границу скорости.
Ученые отмечают, что хоть приближения, использованные в некоторых формулах, и могут повлиять на вычисление v и его оценку, vu все же формируется исходя из фундаментальных констант. Другими словами, в конечном итоге приближения не имеют столь значимого влияния.
Также было установлено, что рассчитанное значение верхней границы скорости звука применимо к твердым телам не только с сильной межатомной связью, но и со слабой. Формула №3, 6 и 7 предполагают, что валентные электроны непосредственно участвуют в связывании. Следовательно, они играют важную роль в системах с металлической, ковалентной и ионной связью. Несмотря на то, что связывание в твердых телах со слабой связью также имеет электромагнитное происхождение, слабые дипольные и ван-дер-ваальсовые взаимодействия приводят к меньшему E и, как результат, меньшему v. Потому из этого следует, что верхняя граница vu применима и к слабосвязанным системам.
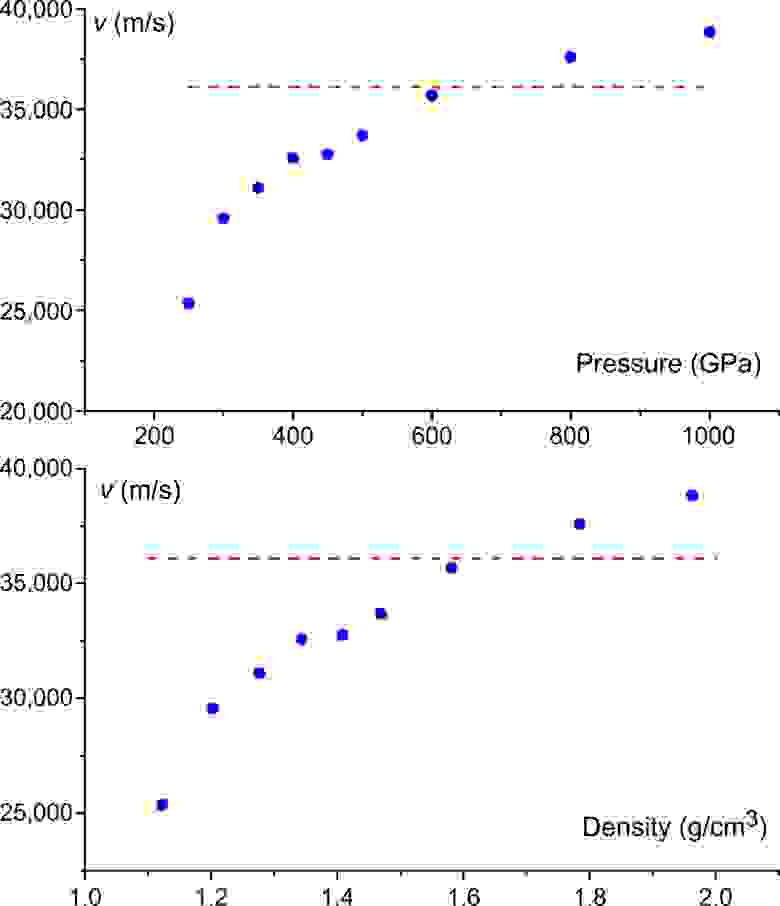
Ученые отмечают, что верхняя граница vu соответствует твердому водороду с прочной металлической связью. Данная фаза вещества существует только при мегабарном давлении и динамически нестабильна при атмосферном давлении, где происходит образование молекул. Посему было решено провести расчеты v в атомарном водороде, чтобы подтвердить верность расчетов как таковых.
Расчеты скорость звука в атомарном водороде проводились с применением структуры I41/amd, которая является наилучшей структурой-образцом для твердого атомарного металлического водорода. Известно, что эта структура становится термодинамически стабильной в диапазоне давлений от 400 до 500 ГПа, ниже которого твердый водород является молекулярным твердым телом. Однако было обнаружено, что I41/amd динамически устойчива при давлениях выше примерно 250 ГПа, поэтому расчеты проводились в диапазоне давления от 250 до 1000 ГПа.
Изображение №3
На графике выше представлена скорость звука как функция давления и плотности. Рассчитанное значение скорости звука было ниже значения vu в широком диапазоне давлений. Увеличение v выше расчетной верхней границы возникает лишь при давлении 600 ГПа и выше. Следовательно, при нормальных условиях скорость звука не будет превышать расчетную верхнюю границу.
Для более подробного ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.
Эпилог
В данном труде ученые определили, что важнейшую роль в оценке максимально возможной скорости звука играют две фундаментальные константы — постоянная тонкой структуры и отношение массы протона к массе электрона.
Проведенные расчеты были проверены на практике с применением разнообразных материалов. Эксперименты позволили установить, что скорость звука должна уменьшаться с атомарной массой. Из этого следует, что максимальная скорость звука достигается в твердом атомарном водороде, который может существовать в таком виде лишь при очень высоком давлении. Тем не менее было установлено, что верхняя граница скорости звука в рамках данного исследования составляет 36100 м/с. С практической точки зрения, подобные исследования крайне важны для понимания тех или иных материалов, а также их свойств.
Естественно, ученые не намерены останавливаться на достигнутом. Их расчеты и соответствующие экспериментальные данные требуют перепроверки, уточнения и дополнительного подтверждения. В будущем данное исследование будет продолжено, а верхняя граница скорости звука может неожиданно сместиться в большую или меньшую сторону ввиду новых данных. Как бы то ни было, фундаментальный подход остается прежним, а сам факт лучшего понимания процессов, протекающих вокруг нас, позволяет с уверенностью смотреть на развитие данного исследования.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. 🙂