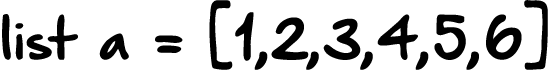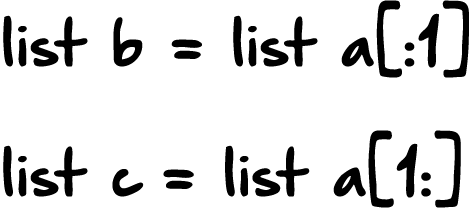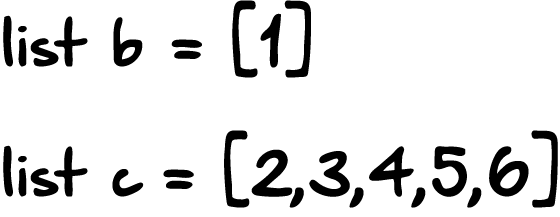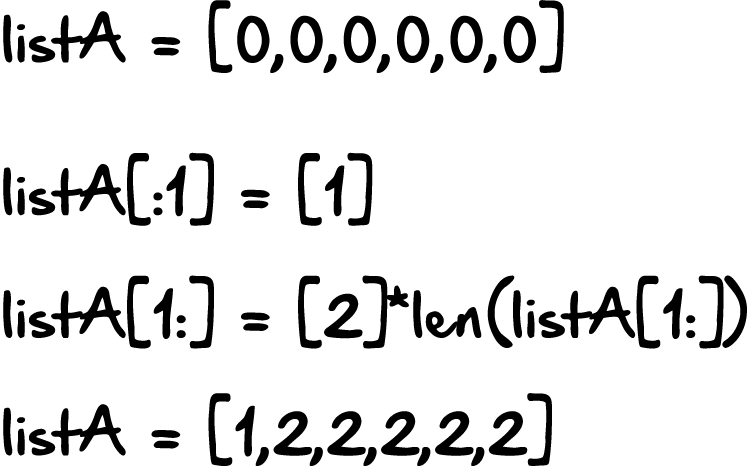что быстрее рекурсия или цикл
Является ли рекурсия быстрее, чем зацикливание?
Я знаю, что рекурсия иногда намного чище, чем зацикливание, и я ничего не спрашиваю о том, когда мне следует использовать рекурсию поверх итерации, я знаю, что уже есть много вопросов по этому поводу.
Что я спрашиваю, так ли рекурсия всегда быстрее, чем цикл? Мне кажется, вы всегда сможете уточнить цикл и заставить его работать быстрее, чем рекурсивная функция, потому что цикл отсутствует, постоянно настраивая новые кадры стека.
Я специально ищу, является ли рекурсия быстрее в приложениях, где рекурсия является правильным способом обработки данных, например, в некоторых функциях сортировки, в двоичных деревьях и т. Д.
Это зависит от используемого языка. Вы написали «независимый от языка», поэтому я приведу несколько примеров.
В Java, C и Python рекурсия довольно дорога по сравнению с итерацией (в целом), потому что она требует выделения нового фрейма стека. В некоторых C-компиляторах можно использовать флаг компилятора, чтобы устранить эти издержки, которые преобразуют определенные типы рекурсии (фактически, определенные типы хвостовых вызовов) в переходы вместо вызовов функций.
Я знаю, что в некоторых реализациях Scheme рекурсия, как правило, будет быстрее, чем зацикливание.
Короче говоря, ответ зависит от кода и реализации. Используйте любой стиль, который вы предпочитаете. Если вы используете функциональный язык, рекурсия может быть быстрее. Если вы используете императивный язык, итерация, вероятно, быстрее. В некоторых средах оба метода приводят к созданию одной и той же сборки (поместите ее в свою трубу и выкурите ее).
рекурсия всегда быстрее, чем цикл?
Нет, Итерация всегда будет быстрее, чем Рекурсия. (в архитектуре фон Неймана)
Объяснение:
Если вы создаете минимальное количество операций с обычного компьютера с нуля, «Итерация» стоит на первом месте в качестве строительного блока и требует меньше ресурсов, чем «рекурсия», следовательно, это быстрее.
Создание псевдо-вычислительной машины с нуля:
Задайте себе вопрос : что вам нужно, чтобы вычислить значение, то есть следовать алгоритму и достичь результата?
Мы создадим иерархию понятий, начиная с нуля и определяя в первую очередь базовые, основные понятия, затем создадим понятия второго уровня с ними и так далее.
а) Установить и переместить ячейки памяти
б) логика и арифметика
Выражение выше подразумевает 3 шага с неявной переменной «result».
Указатель инструкций : если у вас есть последовательность шагов, у вас также есть неявный «указатель инструкций». Указатель инструкции отмечает следующую инструкцию и продвигается после чтения инструкции, но до ее выполнения.
Бесконечная итерация : отскочив назад, теперь вы можете заставить агента «повторить» определенное количество шагов. На данный момент у нас есть бесконечная итерация.
Реализация: (новые концепции не требуются)
Проблема с одноуровневой реализацией: Вы не можете вызвать другую подпрограмму из подпрограммы. Если вы это сделаете, вы перезапишете возвращающий адрес (глобальную переменную), поэтому вы не сможете вкладывать вызовы.
Чтобы иметь лучшую реализацию для подпрограмм: вам нужен STACK
Стек : Вы определяете пространство памяти для работы в качестве «стека», вы можете «выталкивать» значения в стек, а также «выталкивать» последнее «вытолкнутое» значение. Для реализации стека вам понадобится указатель стека (подобный указателю инструкций), который указывает на фактическую «верхушку» стека. Когда вы «нажимаете» значение, указатель стека уменьшается, и вы сохраняете значение. Когда вы «выталкиваете», вы получаете значение в фактическом указателе стека, а затем увеличивается указатель стека.
Рекурсия : что происходит, когда подпрограмма вызывает себя? Это называется «рекурсия».
Проблема: Перезаписывая локальные промежуточные результаты, подпрограмма может быть сохранена в памяти. Поскольку вы вызываете / повторно используете одни и те же шаги, если промежуточный результат хранится в предопределенных ячейках памяти (глобальных переменных), они будут перезаписаны при вложенных вызовах.
Достигнув рекурсии, мы останавливаемся здесь.
Вывод:
Итерация всегда будет быстрее в машинном коде, потому что она подразумевает меньше инструкций и, следовательно, меньше циклов ЦП.
Какой лучше»?
Вам следует использовать «итерацию», когда вы обрабатываете простые последовательные структуры данных, и везде будет работать «простой цикл».
Вы должны использовать «рекурсию», когда вам нужно обработать рекурсивную структуру данных (мне нравится называть их «фрактальными структурами данных»), или когда рекурсивное решение явно более «элегантно».
Совет : используйте лучший инструмент для работы, но понимайте внутреннюю работу каждого инструмента, чтобы выбирать мудро.
Рекурсия может быть быстрее, если альтернативой является явное управление стеком, как в алгоритмах сортировки или двоичного дерева, о которых вы упомянули.
У меня был случай, когда переписывание рекурсивного алгоритма в Java сделало его медленнее.
Таким образом, правильный подход заключается в том, чтобы сначала написать его наиболее естественным образом, оптимизировать только в том случае, если профилирование показывает его критичность, а затем измерить предполагаемое улучшение.
Почему циклы быстрее, чем рекурсия?
На практике я понимаю, что любая рекурсия может быть записана как цикл (и наоборот (?)), И если мы проводим измерения на реальных компьютерах, мы обнаруживаем, что циклы быстрее, чем рекурсия для той же проблемы. Но есть ли какая-либо теория, которая делает это различие, или это в основном эмпирический?
Причина, по которой циклы быстрее рекурсии, проста.
Петля выглядит так в сборке.
Один условный переход и некоторая бухгалтерия для счетчика цикла.
Рекурсия (когда она не оптимизирована или не может быть оптимизирована) выглядит следующим образом:
Это намного сложнее, и вы получаете по крайней мере 3 прыжка (1 тест, чтобы увидеть, были ли выполнены, один вызов и один возврат).
Также в рекурсии параметры должны быть установлены и извлечены.
Ничего из этого не требуется в цикле, потому что все параметры уже настроены.
Теоретически параметры могут оставаться на месте и при рекурсии, но никакие компиляторы, о которых я знаю, на самом деле не заходят так далеко в своей оптимизации.
Пример плохой обработки рекурсии Например, если передан параметр, который подсчитан по ссылке (например, неконстантный параметр управляемого типа), он добавит 100 циклов, выполняя заблокированную настройку подсчета ссылок, полностью убивая производительность по сравнению с циклом.
На языках, настроенных на рекурсию, такого плохого поведения не происходит.
Оптимизация ЦП
Другая причина, по которой рекурсия медленнее, заключается в том, что она работает против механизмов оптимизации в ЦП.
Возвращения могут быть предсказаны правильно, только если их не слишком много в ряду. ЦП имеет буфер стека возврата с (несколькими) горстками записей. Как только они закончатся, каждый дополнительный возврат будет неверно предсказан, что приведет к огромным задержкам.
На любом процессоре, который использует рекурсию на основе буфера возврата стека, которая превышает размер буфера, лучше избегать.
О тривиальных примерах кода с использованием рекурсии
Если вы используете тривиальный пример рекурсии, такой как генерация чисел Фибоначчи, то эти эффекты не возникают, потому что любой компилятор, который «знает» о рекурсии, преобразует его в цикл, как любой программист, достойный его внимания было бы.
Если вы запустите эти тривиальные примеры в среде, которая не оптимизируется должным образом, то стек вызовов (излишне) вырастет за пределы.
О хвостовой рекурсии
Обратите внимание, что иногда компилятор оптимизирует удаленную хвостовую рекурсию, превращая ее в цикл. Лучше всего полагаться на это поведение только в тех языках, которые имеют хорошую репутацию в этом отношении.
Многие языки вставляют скрытый код очистки перед окончательным возвратом, предотвращая оптимизацию хвостовой рекурсии.
Путаница между истиной и псевдо-рекурсией
Если ваша среда программирования превращает ваш рекурсивный исходный код в цикл, то, возможно, это не настоящая рекурсия, которая выполняется.
Настоящая рекурсия требует хранения хлебных крошек, чтобы рекурсивная процедура могла отслеживать свои шаги после выхода.
Именно обработка этого следа делает рекурсию медленнее, чем использование цикла. Этот эффект усиливается текущими реализациями CPU, как описано выше.
Влияние среды программирования
Если ваш язык настроен на оптимизацию рекурсии, тогда непременно используйте рекурсию при каждой возможности. В большинстве случаев язык превратит вашу рекурсию в некий цикл.
В тех случаях, когда это невозможно, программисту будет сложно. Если ваш язык программирования не настроен на рекурсию, то этого следует избегать, если домен не подходит для рекурсии.
К сожалению, многие языки плохо справляются с рекурсией.
Неправильное использование рекурсии
Нет необходимости вычислять последовательность Фибоначчи с использованием рекурсии, фактически это патологический пример.
Рекурсию лучше всего использовать в языках, которые ее явно поддерживают, или в областях, где рекурсия сияет, например при обработке данных, хранящихся в дереве.
Я понимаю, что любая рекурсия может быть записана как цикл
Да, если вы готовы поставить телегу перед лошадью.
Все экземпляры рекурсии могут быть записаны как цикл, некоторые из них требуют использования явного стека, например хранилища.
Если вам нужно свернуть свой стек только для того, чтобы превратить рекурсивный код в цикл, вы также можете использовать простую рекурсию.
Если, конечно, у вас нет особых потребностей, таких как использование перечислителей в древовидной структуре, и у вас нет надлежащей языковой поддержки.
Эти другие ответы несколько вводят в заблуждение. Я согласен, что они заявляют детали реализации, которые могут объяснить это несоответствие, но они преувеличивают случай. Как правильно предложено jmite, они ориентированы на реализацию для неработающих реализаций вызовов функций / рекурсии. Многие языки реализуют циклы с помощью рекурсии, поэтому циклы явно не будут быстрее в этих языках. Рекурсия ни в коем случае не менее эффективна, чем зацикливание (если применимо оба) в теории. Позвольте мне процитировать тезис к статье Гая Стила 1977 года « Разоблачение мифа о« дорогостоящем вызове процедуры »или, реализация процедур, считающихся вредными, или, Лямбда: окончательный вариант GOTO
Фольклор утверждает, что операторы GOTO «дешевы», а вызовы процедур «дороги». Этот миф в значительной степени является результатом плохо разработанных языковых реализаций. Исторический рост этого мифа считается. Обсуждаются как теоретические идеи, так и существующая реализация, которые развенчивают этот миф. Показано, что неограниченное использование процедурных вызовов обеспечивает большую стилистическую свободу. В частности, любая блок-схема может быть написана как «структурированная» программа без введения дополнительных переменных. Сложность с оператором GOTO и вызовом процедуры характеризуется как конфликт между абстрактными концепциями программирования и конкретными языковыми конструкциями.
Теперь для примера. Определить fact как
Вы можете увидеть из фигуры, даже не глядя на детали, что рост отсутствует, и каждой итерации требуется одинаковое количество места. (Технически, числовой результат растет, что неизбежно и так же верно для while цикла.) Я не хочу, чтобы вы указывали на безгранично растущий «стек» здесь.
Кажется, что архетипическая семантика лямбда-исчисления уже выполняет то, что обычно называют «оптимизацией хвостового вызова». Конечно, никакой «оптимизации» здесь не происходит. Здесь нет особых правил для «хвостовых» вызовов, в отличие от «обычных» вызовов. По этой причине трудно дать «абстрактную» характеристику того, что делает хвостовой вызов «оптимизация», так как во многих абстрактных характеристиках семантики вызова функций нет ничего, что хвостовой вызов «оптимизации» мог бы сделать!
То, что аналогичное определение fact во многих языках «переполнение стека», является неспособностью этих языков правильно реализовать семантику вызова функций. (У некоторых языков есть оправдание.) Ситуация примерно аналогична языковой реализации, в которой реализованы массивы со связанными списками. Индексирование в такие «массивы» будет тогда операцией O (n), которая не соответствует ожиданиям массивов. Если бы я сделал отдельную реализацию языка, которая использовала бы реальные массивы вместо связанных списков, вы бы не сказали, что я реализовал «оптимизацию доступа к массивам», вы бы сказали, что я исправил неправильную реализацию массивов.
На практике распространенность нарушенных реализаций вызовов функций обусловлена тремя основными факторами. Во-первых, многие языки наследуют сломанную реализацию от языка реализации (обычно C). Во-вторых, детерминистическое управление ресурсами приятно и делает проблему более сложной, хотя это предлагают только несколько языков. В-третьих, и, по моему опыту, причина, по которой большинство людей волнуется, заключается в том, что им нужны трассировки стека при возникновении ошибок в целях отладки. Только вторая причина может быть теоретически мотивированной.
Рекурсия и цикл, в чем разница? На примере Python
Цикл — это фундаментальный инструмент в программировании. Существует множество различных типов циклов, но почти все они выполнят одну базовую функцию: повторение определённых действий над данными, для их анализа или управления ими. Рекурсия, так же распространённый способ анализировать и манипулировать данными, как и цикл, но как правило, менее понятный и часто более запутанный. Почти все рекурсивные функции можно переписать в циклы, и наоборот. Тем не менее, каждый тип функции имеет свои преимущества и недостатки, и сегодня вы узнаете, в каких случаях применять тот или иной метод. В статье мы разберём следующие вопросы:
Начнём с метода, который кажется более простым из этих двух.
Циклы for
Цикл for используют для перебора последовательности данных (списка, кортежа, словаря, набора или строки). При достижении конца последовательности цикл завершается.
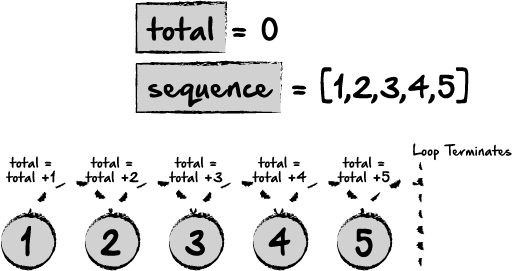
Например, вам нужно сложить числа от 1 до 5 и получить их сумму. Конечно, вы можете просто суммировать 1+2+3+4+5. Но, создать функцию намного удобнее, потому что вы сможете использовать её повторно, причём подставляя любые значения, даже если они не известны заранее.
Это будет выглядеть примерно так:
Для работы такого цикла, нам нужно хранить список всех чисел, чтобы мы могли перебирать элементы и складывать их в итоговое значение.
Вот как это выглядит в коде:
Запустив код, мы увидим, что все числа на своих местах и нам возвращается их сумма.
Вывод функции:
Рекурсия
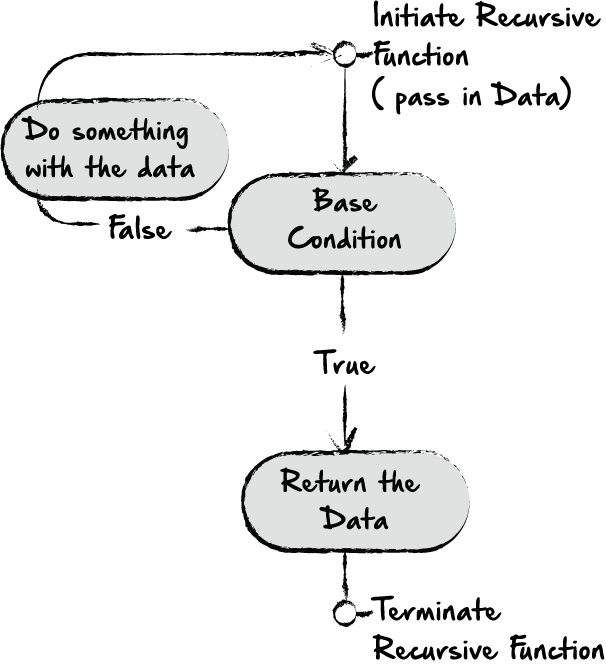
Если функция вызывает сама себя, то это является признаком рекурсии. Одно из важнейших отличий рекурсии от цикла, это способ завершения рекурсивной функции. В приведённом выше примере цикл for завершается в конце последовательности, в которой он выполняется. А вот рекурсивная функция может продолжаться бесконечно, потому что она может не иметь последовательности данных. Вместо этого у рекурсивной функции есть так называемое базовое условие. Базовое условие определяет, когда цикл должен завершится.
Давайте попробуем решить предыдущую задачу рекурсивным способом. Визуально это выглядит так:
Каждый раз функция либо вызывает себя с новыми входными данными, либо возвращает значение.
Вот как это выглядит в коде:
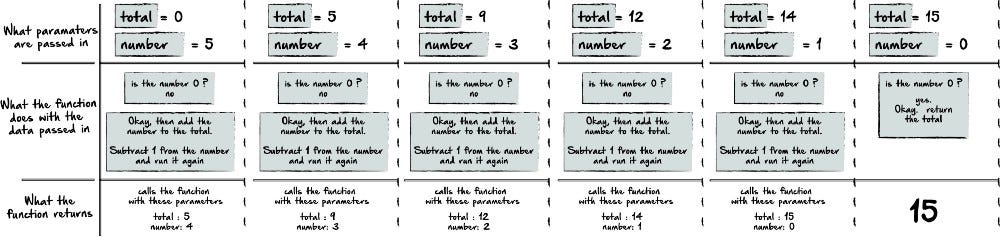
Как видите мы передаём два значения: начальное и итоговое. При первом вызове функции итоговое значение равно 0, а начальное 5. Мы проверяем, является ли начальное число 0. Если нет, то вызываем функцию снова, но на этот раз мы меняем входное значение на 5–1 и 0+5, и повторяем этот процесс до тех пор, пока n не будет равно 0. После выполнения этого условия мы возвращаем итоговое значение (15).
Вычисление сложного процента рекурсией и циклом FOR
Давайте разберём более сложную задачу. Нужно определить стоимость кредита или инвестиции со сложным процентом. Чтобы это сделать, нам нужны следующие данные:
Формула расчёта сложного процента:
Так мы можем рассчитать всю сумму сразу. Но вместо этого, для расчёта мы используем цикл или рекурсию. В таком случае переменная времени (nt) будет обрабатываться в итерациях.
Давайте сразу создадим переменные, в которых будем хранить исходные числа и используем их в обоих методах:
Расчёт по сложной процентной ставке итеративно
Давайте сразу посчитаем общее количество платежей, чтобы упростить вычисление в цикле. Так как платежи ежемесячные, а количество лет равно 10, то результат будет 120, или 10*12. Теперь мы можем вычислять процент для каждого месяца и добавлять результат каждой итерации к основной сумме.
Так выглядит код:
Единственное различие между этим и предыдущим примерами заключается в том, что мы делаем на несколько вычислений больше во время каждой итерации. Также увеличилось число итераций с 5 до 120.
Результат наших вычислений:
Расчёт по сложной процентной ставке рекурсивным способом
В предыдущем примере последовательность данных равна 120, что отражает количество раз, когда основная сумма пересчитывается. Цикл прерывается по завершении последовательности. Рекурсивный метод позволяет нам поступить схожим образом, т.е. инициализировать счётчик и задать два условия.
Выполнить вычисление сложного процента. Добавить результат вычисления к общей сумме. Уменьшить значение счётчика на 1. Повторить те же действия, подставив новое значения для счётчика и общей суммы.
Возврат общей суммы
В предыдущем примере, цикл функции начинался со значения 5 и завершался при 0.
Здесь происходит тоже самое, только начальное значение теперь 120
Здесь мы либо снова вызываем функцию, либо возвращаем обновлённую общую сумму. Каждый раз вызывая функцию, значение счётчика уменьшается на 1. Возврат общей суммы происходит, когда счётчик равен 0.
Когда использовать рекурсию
Выбор между рекурсивным и итеративным методом может в значительной степени зависеть от языка, который вы используете, или от задачи, которую вы намерены решить. Например, в JavaScript рекурсия может привести к ошибкам stack frame errors, когда предел стека уже достигнут, а базовое условие ещё не выполнено. В таком случае, итеративный подход будет работать лучше.
Рассмотренный выше случай является хорошим примером того, когда рекурсия работает намного лучше, чем цикл.
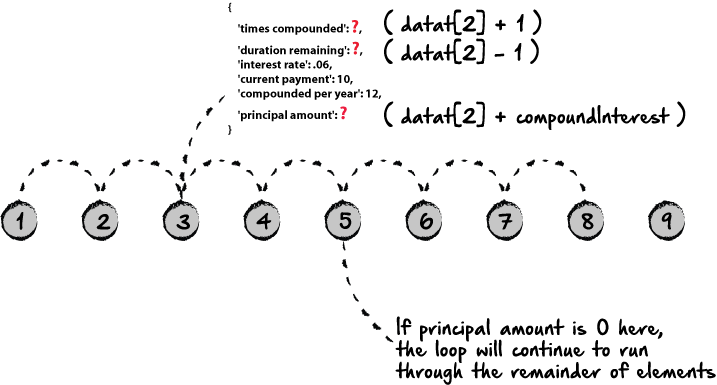
Давайте представим, что помимо тех чисел, которые мы использовали в предыдущем примере, нам нужно учитывать и другие данные. Например, мы можем отслеживать то, как регулярные платежи влияют на срок кредита. Возможно, мы захотим остановить цикл до завершения последовательности. Если общее количество раз, когда начисляются проценты по кредиту равно 120, то и длина списка равна 120. Но, если сумма кредита будет равна 0 уже после 100 итераций, то в конце списка останется 20 неиспользуемых и ненужных элементов списка. Проблема дальнейшего усложнения сценария цикла заключается в том, что значения переменных, таких как сумма кредита, зависит от значения той же переменной на предыдущей итерации. Дело не в том, что это сложно реализовать, а в том, что это грязно.
Визуализация данной проблемы:
Рекурсивные структуры данных
Именно в таких случаях рекурсивные структуры данных особенно полезны. Структуру можно назвать рекурсивной, если её можно определить в терминах меньшей версии самой себя. Список является примером рекурсивной структуры данных.
Например, возьмём такой список:
Теперь, сделаем на его основе два меньших списка:
Если вывести оба списка, то мы увидим следующее:
Благодаря рекурсивным функциям и рекурсивными структурам данных мы можем изменить весь список или меньшую часть большего списка за раз. Итеративный подход решения подобной проблемы, позволяет изменить только одно значение в одном индексе за раз.
Пример того, как это сделать:
Сохранив маленькие части большого списка, мы можем вызвать ту же функцию (рекурсия) и отправить ей эти части (рекурсивная структура данных).
Вот как это работает на примере с вычислением сложного процента:
Наша функция в основном состоит из операторов if и else. Мы можем усложнить эту структуру если понадобится, но она и в таком виде делает всё что нам нужно. В итоге, мы хотим вернуть окончательные данные, которые покажут нам сумму кредита и размер текущего платежа на каждой итерации, когда начисляется процент.
Выходные данные:
Визуализация процессов рекурсивной функции:
При каждом рекурсивном вызове мы будем брать первый элемент массива из списка. Затем мы изменим значения этого элемента и снова вызовем функцию, но на этот раз передадим ей в качестве параметров array[:1] и array[1:]. На картинке видно, что, достигнув середины списка, мы будем иметь две его части одинакового размера. А уже к концу мы полностью переберём и модифицируем все элементы первого списка, и добавим их во второй список. Далее мы шаг за шагом реализуем эту функцию в коде.
Шаг 1: создаём массив
На данном этапе, наш массив имеет длину равную числу раз, когда начисляется процент. Каждый элемент содержит одинаковые данные, которые мы будем изменять рекурсивно.
Шаг 2: создаём функцию и базовое условие
Базовое условие будет учитывать два возможных сценария. Либо счётчик достигнул конца последовательности ( len(inputArr) == 0 ), либо мы погасили кредит раньше ( inputArr[-1][‘principal amount’] ).
Шаг 3: создаём выражение else и определяем переменные current, inputArray и outputArray
Шаг 4: если массив outputArray пуст, то берём первый элемент из массива входных данных и помещаем его в массив выходных данных без изменений.
Теперь оба массива выглядят как на картинке, которую вы видели выше, в момент первого вызова рекурсивной функции.
Шаг 5: если массив выходных данных не пуст, то изменяем все значения текущего элемента.
Шаг 6: добавляем переменную newCurrent к массиву outputArray
Шаг 7: вызываем рекурсивную функцию с новыми параметрами
Мы закончили! Так выглядит код целиком:
Чтобы убедиться, что код работает так, как мы задумали, давайте увеличим сумму платежа.
Если изменить сумму платежа на 2000, то при выводе должны получиться такие данные:
Такой код возвращает более чистый результат, чем при использовании цикла. Если бы мы использовали итеративный подход, то нам пришлось бы перебрать все 120 элементов, большинство из которых были бы бесполезны/пусты.
Заключение
На первый взгляд рекурсия может показаться сложной. Но в некоторых случаях, рекурсивный метод невероятно эффективен, если всё сделать правильно. Тем не менее, иногда лучше использовать циклы. Понимание обоих методов и умение эффективно их использовать поможет вам в работе и будет преимуществом на собеседовании.