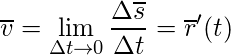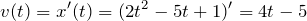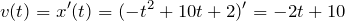чем на графике ускорения выражается мгновенная скорость
1. МЕХАНИКА
1.1. Кинематика
Движение с ускорением
Равноускоренное прямолинейное движение – движение по прямой с постоянным ускорением (а = const ).
Ускорение а (размерность: м/с 2 ) – векторная физическая величина, показывающая, на сколько изменяется скорость тела за 1 с.
В проекции на ось ОХ формула аналогичная
Знаки проекции ускорения зависят от направления вектора ускорения и оси – сонаправлены они или направлены противоположно.
Измерительный прибор – акселерометр. (В ЕГЭ по физике есть вопросы, каким прибором что измеряют.)
График ускорения – зависимость проекции ускорения от времени:
График ускорения при равноускоренном прямолинейном движении – прямая, параллельная оси времени (1, 2).
Чем дальше график от оси времени (2), тем больше модуль ускорения.
Скорость при равноускоренном прямолинейном движении.
В векторном виде,
в проекции на ось OX,
с учетом знака ускорения («+» разгон, «-» торможение):

График мгновенной скорости – зависимость проекции скорости от времени.
График скорости при равноускоренном прямолинейном движении – прямая (1, 2, 3). Если график располагается над осью времени, то тело движется по направлению оси ОХ.
Чем больше угол наклона графика (3), тем больше модуль ускорения.
Если график пересекает ось времени (2), то на первом этапе тело тормозило, в какой-то момент скорость его стала равной нулю, и далее тело двигалось ускоренно в противоположную сторону.
Геометрический смысл перемещения
Модуль перемещения при равноускоренном прямолинейном движенииравен площади трапеции под графиком скорости.
Формулы для определения кинематических величин равноускоренного прямолинейного движения:

«Без ускорения» и «без времени» означает, что в этих формулах не фигурирует ускорение и время, но это не значит, что ускорение равно нулю.
Цветом выделены основные формулы, остальные легко выводятся из них.
Уравнение координаты при равноускоренном прямолинейном движении позволяет определить кинематические величины равноускоренного прямолинейного движения даже в тех случаях, когда направление движения меняется:
Графики кинематических величин прямолинейного движения.
Их ндо уметь читать и рисовать. По горизонтальной оси обычно время. По вертикальной оси. будьте внимательны!
Свободное падение
Это частный случай движения с ускорением.
Свободное падение происходит под действием только силы тяжести. Подробнее о связи силы с ускорением будет в теме «Динамика», второй закон Ньютона.
Сопротивление воздуха обычно не учитывается.
Все тела независимо от массы падают (в вакууме или без учета сопротивления воздуха) с одинаковым ускорением.
Свободное падение по вертикали – пример равноускоренного прямолинейного движения.
В задачах на свободное падение единицы измерения всех величин сразу следует переводить в СИ.
Уравнение координаты при свободном падении позволяет определить кинематические величины свободного падения даже в тех случаях, когда направление движения изменяется. Уравнение координаты позволяет определить высоту тела в любой момент времени.
В разделе «Динамика» рассмотрим более сложные случаи:
— Тело подбросили от земли и поймали на некоторой высоте.
— Тело подбросили от земли, на одной и той же высоте оно побывало дважды.
— Горизонтальный бросок (движение по параболе). Бросок под углом к горизонту.
Мгновенная скорость движения
Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.
Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.
Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.
Имеет ли понятие «мгновенной скорости» физический смысл? Скорость – это характеристика изменения перемещения тела в пространстве. Однако, для того, чтобы определить, как изменилось перемещение, необходимо наблюдать за движением в течение некоторого времени. Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть достаточно малый 
Примеры решения задач по теме «Мгновенная скорость»
| Задание | О какой скорости – средней или мгновенной – идет речь в следующих случаях: |
1) самолет летит из Санкт-Петербурга в Москву со скоростью 800 км/ч;
2) пуля вылетает из винтовки со скоростью 800 м/с;
3) велосипедист едет по шоссе со скоростью 12 км/ч;
4) прибор показывает скорость тепловоза 75 км/ч?
2) и 4) – речь идет о мгновенной скорости.
| Задание | Закон движения точки по прямой задается уравнением 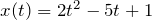 . Найти мгновенную скорость точки через 10 секунд после начала движения. . Найти мгновенную скорость точки через 10 секунд после начала движения. |
| Решение | Мгновенная скорость точки – это первая производная радиус-вектора по времени. Поэтому для мгновенной скорости можно записать: |
Через 10 секунд после начала движения мгновенная скорость будет иметь значение:
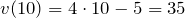
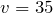 м/с.
м/с.| Задание | Тело движется по прямой так, что его координата 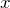 (в метрах) изменяется по закону (в метрах) изменяется по закону 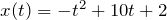 . Через сколько секунд после начала движения тело остановится? . Через сколько секунд после начала движения тело остановится? |
| Решение | Найдем мгновенную скорость тела: |
В момент остановки мгновенная скорость тела будет равна нулю:
Ускорение при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v 0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Запишем исходные данные:
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
Подставляем данные формулу и вычисляем модуль ускорения:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Чем на графике ускорения выражается мгновенная скорость
Если взять длину отрезка пути, пройденного телом, измеренного в метрах, (в нашем случае, для простоты, «материальной точкой». То есть телом, размерами которого можно пренебречь в данной конкретной задаче) и разделить на время, затраченное на прохождение этого отрезка пути в секундах, то полученная величина будет являться «средней скоростью» тела на данном отрезке пути.
Почему средней, надеюсь, понятно?
Соответственно, если мы рассмотрим отрезок пути произвольно движущегося тела и отсечем время, за которое это тело преодолеет данный участок пути, а потом разделим на это время длину отрезка пути, то получим некую величину с размерностью скорости. Метры в секунду.
Черточка над v означает, что это средняя скорость.
Если мы рассмотрим две половины данного отрезка и, соответственно два времени прохождения этих отрезков телом, то мы получим две скорости (средние скорости на каждом отрезке), которые в реальном движении не будут равны между собой и не будут равны средней скорости на целом отрезке. При этом, заметим, что сумма двух половин отрезка пути равна длине всего отрезка, а сумма времен равна времени прохождения всего отрезка.
Сравнив их, мы сможем сделать выводы на каком участке тело двигалось быстрее, а на каком медленнее.
Теперь представим себе, что мы разделили наш целый отрезок пути на бесконечно маленькие отрезки и измерили время прохождения каждого бесконечно маленького отрезка, а, затем, разделили путь на время на каждом бесконечно малом отрезке.
Что мы получим в результате?
Бесконечно малый отрезок 
Разберемся в этом подробнее.
Представить себе деление бесконечно малого расстояния на бесконечно малое время (Подумайте сами, почему время тоже бесконечно малое!) не очень то легко.
Это очень просто представить, как процесс, изображенный на рисунке 3. Возьмем какой-либо маленький отрезок (отрезок пути в смысле рассматриваемой нами задачи) и разделим его на время прохождения нашим телом этого отрезка. Получим среднюю скорость тела на этом отрезке. Это мы уже знаем.
А дальше продолжим этот процесс много-много раз. Одна восьмая, одна шестнадцатая, одна тридцать вторая, одна шестьдесят четвертая, и т.д. Нужно отметить, что мы очень быстро будем брать в рассмотрение настолько маленькие отрезки, что средняя скорость на этих все меньших и меньших отрезках с какого-то момента перестанет в наших измерениях меняться.
. В реальном эксперименте мы можем остановить наш процесс по нескольким причинам.
Может оказаться, что после какого-то очередного деления отрезка и измерения средняя скорость тела в каждом последующем измерении (на каждом последующем отрезке, в качестве которого мы берем первую половину предыдущего отрезка) после каждого очередного деления перестанет изменяться с точностью до нужного количества знаков после запятой.
В этом случае мы можем договориться (сами с собой), что наш процесс можно остановить, а полученную величину считать мгновенной скоростью в точке начала нашего первого отрезка пути.
. При этом мы производим допущение, что дальнейший (бесконечный) процесс деления отрезков и измерения средних скоростей на их первых половинках (половинках, примыкающих к началу первого отрезка пути) не приведет к изменению значения средних скоростей с требуемой нами точностью.
По сути, мы заменили бесконечный процесс конечным алгоритмом действий.
Таким образом, мы договариваемся считать результат этого вышеописанного конечного процесса равным результату деления бесконечно малого отрезка пути на бесконечно малое время прохождения этого отрезка телом.
В строгом математическом виде пишется:
Читается: «предел функции 

Эту величину мы пока условимся называть «мгновенной скоростью тела в точке».
Но процесс вычисления мгновенной скорости можно себе представить и по-другому. Мы делили на отрезки путь. А можно делить отрезок времени. И это будет правильно с точки зрения физики. Делить, все ближе и ближе приближаясь к моменту времени, для которого мы хотим определить мгновенную скорость.
А теперь устремляем наш отрезок времени к нулю. Т.е. делаем его все меньше и меньше (главное, чтобы наша точка, в которой вычисляем мгновенную скорость всегда была в пределах этого отрезка, например, в начале). Еще меньше. И еще меньше!
Насколько меньше? Очень, очень, очень маленьким! Бесконечно малым.
Это очень просто определить чисто математически: «Бесконечно малая величина – это величина меньшая, чем любая, сколь угодно малая конечная величина». Что это означает?
Очень просто. Берем любой самый маленький конечный отрезок времени. Его можно записать в виде числа секунд, например. Одна миллисекунда – это одна тысячная секунды. Наш бесконечно малый отрезок строго меньше одной миллисекунды. И одной миллиардной секунды (микросекунды). И одной наносекунды! И вообще, если даже мы напишем на большой стене число с миллионами нулей после запятой, то и тогда наша бесконечно малая величина будет строго меньше!
Обозначается бесконечно маленький отрезок времени dt (маленькая латинская буква d вместо ∆ , которая обычно означает конечность отрезка). Догадайтесь самостоятельно, почему отрезок пути, пройденный телом за бесконечно малый отрезок времени, тоже бесконечно малый! Операция деления бесконечно малого отрезка пути на бесконечно малый отрезок времени записывается
Если у нас есть функция зависимости координаты от времени X ( t ), то проделав для каждого значения t операцию нахождения мгновенной скорости, мы получим функцию V ( t ) – функцию зависимости мгновенной скорости тела от времени. Математически мы запишем формулу
Договоримся в нашей книге обозначать производную по времени точкой, а производные по другим величинам, кроме времени штрихом!
Возникает вопрос, а зачем мы все это записали, если мы все равно не сможем повторить операцию нахождения мгновенной скорости для каждой точки – их же бесконечное количество?
Например, пусть мы знаем зависимость координаты от времени
Тогда мы можем тут же вычислить зависимости скорости
Это круто! Потому, что если нам известна функция зависимости координаты от времени, находя производную этой функции по времени, мы сразу же узнаем мгновенную скорость в каждый момент времени.
Подробнее на операции дифференцирования мы остановимся позже. Пока лишь добавим, что функция X ( t ) по отношению к функции V ( t ) называется «первообразной функции V ( t ) ». Обратная операция (нахождение функции, которая после дифференцирования становится производной) называется нахождение первообразной или интегрирование.
Чем замечательна «производная», мы показали. А чем замечательна «первообразная»?
Первообразная функции позволяет найти саму функцию с точностью до некоторой постоянной величины. Таким образом, зная вид производной функции, мы знаем вид самой функции, но с некоторой неопределенностью на постоянную величину.
Мы можем найти функцию координаты X ( t ) = Первообразная ( V ( t )) + const . (где const – обозначение в формулах некоторой постоянной величины) Обычно операцию интегрирования функции записывают с помощью знака интеграла. Он похож на английскую букву S от слова «СУММА».
Таким образом, функция скорости V ( t ) есть производная функции координаты X ( t ) по времени и одновременно первообразной функции ускорения a ( t ) по времени.
Функция ускорения a ( t ) есть производная функции скорости V ( t ) по времени. И одновременно второй производной функции координаты X ( t ) по времени. И т.д.
Надеюсь, теперь у вас сформировалось начальное понимание, что такое «скорость» и «ускорение» в точном физическом смысле. В смысле, удобном для решения задач на движение тел.
Собственно, это все, что нужно знать про механическое движение для успешного решения задач школьной (и любой другой) Механики!
И в заключение. Самое важное в данном параграфе, следующее:
Рассмотрим функцию зависимости координаты тела (материальной точки) от времениX(t).
Зная ее, мы знаем положение тела в каждый момент времени t.
Оказывается, существует простой способ получения из этой функции X(t) другой функцииV(t), которая является функцией зависимости мгновенной скорости тела от времени.
Операция получения функции скорости из функции координаты называется «Дифференцирование». А функция, полученная путем такой операции, называется «Производная» первоначальной функции.
Таким образом говорят, что скорость есть первая производная пути.
Подробнее это будет рассмотрено ниже.
. И еще одно важное замечание. До сих пор шла речь о скорости механического движения. Но все наши рассуждения полностью справедливы для скорости изменения любой другой физической величины. Если известна функция зависимости одной физической величины от другой физической величины, называемой «переменной» (от любой другой, а не только от времени), то производная функции по этой переменной есть функция скорости изменения физической величины в зависимости от изменения нашей переменной.
Забегая вперед приведем пример: Представим, что для каждой точки пространства определена температура вещества в этой точке. И нам известна функция распределения температуры в зависимости от изменения координаты точки. Тогда мы можем вычислить функцию зависимости скорости изменения температуры при пространственном сдвиге по координате (так называемого «пространственного градиента температуры»). Она есть производная нашей функции зависимости температуры от координаты по этой координате.