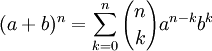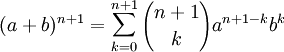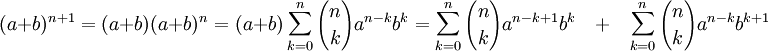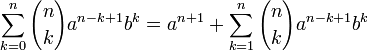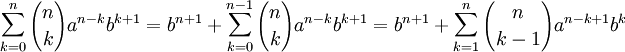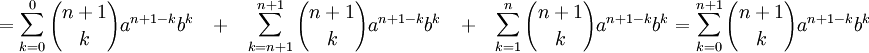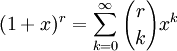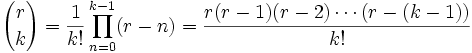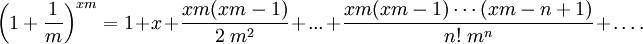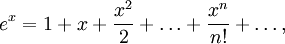Бином ньютона что это такое

Бином ньютона

Бином Ньютона — это формула

,

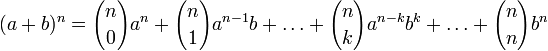
где 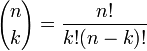— биномиальные коэффициенты, n — неотрицательное целое число.

Содержание

Доказательство

Докажем это равенство, используя метод математической индукции:

Пусть утверждение для n верно:

Тогда надо доказать утверждение для n + 1 :

Извлечём из первой суммы слагаемое при k = 0

Извлечём из второй суммы слагаемое при k = n

Теперь сложим преобразованные суммы:

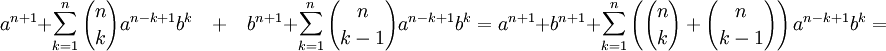
Что и требовалось доказать

— одно из тождеств биномиальных коэффициентов

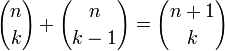
Для ненатуральных степеней

где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты находятся по формуле:

.

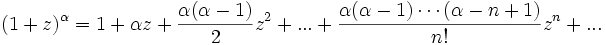
сходится при .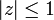

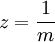
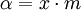
В частности, при и получается тождество

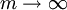
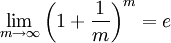
Переходя к пределу при и используя второй замечательный предел , выводим тождество

именно таким образом впервые полученное Эйлером.

История

Считается, что эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Тем не менее, она была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке. Возможно, её открыл персидский учёный, поэт и философ Омар Хайям.

Исаак Ньютон обобщил формулу для прочих показателей степени.

В художественной литературе

В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.

Об этой специфической роли бинома Ньютона в культуре писал известный математик В. А. Успенский [1].

См. также

Полезное

Смотреть что такое «Бином ньютона» в других словарях:

бином ньютона — БИНОМ, а, м. (или бином ньютона). Ирон. О чем л. кажущемся сложным, запутанным. Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита» … Словарь русского арго

БИНОМ НЬЮТОНА — БИНОМ НЬЮТОНА, математическое правило разложения алгебраического выражения (а+b)n в ряд степеней численных значений х и у (где n положительное число). При n 2 разложение выглядит таким образом: (х+у)2=х2+2ху+у2 … Научно-технический энциклопедический словарь

Бином Ньютона — алгебраическая формула, открытая Ньютоном, выражающая какую угодно степень двучлена, а именно: (х + а)n = хn + n/1(axn 1) + [n/(n 1)/1.2](а2хn 2) + …[n(n 1)(n 2)…(n m+1)/1.2.3…m](anxn m) + … или, в компактной форме, пользуясь символом n! =… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Бином Ньютона — Разг. Шутл. О чём л. сложном, запутанном. Елистратов, 41 … Большой словарь русских поговорок

Подумаешь, бином Ньютона! — Из романа (гл. 18 «Неудачливые визитеры») «Мастер и Маргарита» (1940) Михаила Афанасьевича Булгакова (1891 1940). Слова Коровьева Фагота, комментирующего диалог между Воландом и буфетчиком Андреем Фокичем Соковым. Последний пришел жаловаться на… … Словарь крылатых слов и выражений

бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка

БИНОМ — (от лат. bis дважды, и греч. nomos часть, отдел). Двучлен (в алгебре). Бином Ньютона общая формула для возведения двучленного количества в любую степень. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИНОМ в… … Словарь иностранных слов русского языка

Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия

Источник

Бином Ньютона.

Навигация по странице.

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.

Треугольник Паскаля.

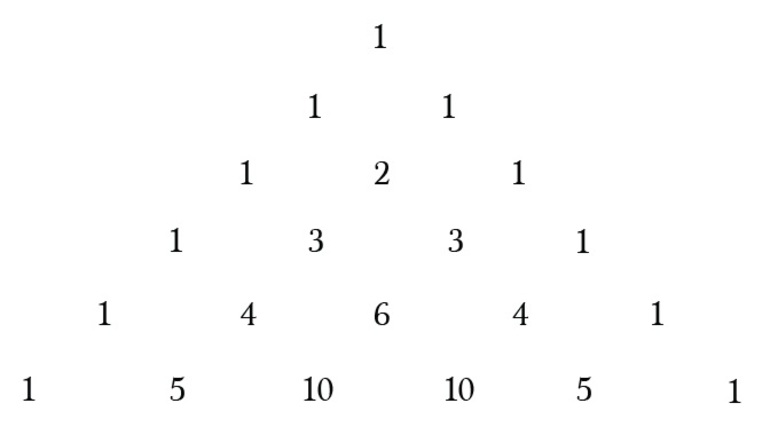
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:

Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n :

Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Свойства биномиальных коэффициентов.

Первые два свойства являются свойствами числа сочетаний.

Доказательство формулы бинома Ньютона.

Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства .

Получили верное равенство.

Докажем, что верно равенство , основываясь на предположении второго пункта.

Поехали!

Раскрываем скобки

Группируем слагаемые

Так как и , то ; так как и , то ; более того, используя свойство сочетаний , получим

Подставив эти результаты в полученное выше равенство

придем к формуле бинома Ньютона .

Этим доказана формула бинома Ньютона.

Рассмотрим подробные решения примеров, в которых применяется формула бинома Ньютона.

Напишите разложение выражения (a+b) 5 по формуле бинома Ньютона.

Найдите коэффициент бинома Ньютона для шестого члена разложения выражения .

В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Доказать, что значение выражения , где n – натуральное число, делится на 16 без остатка.

Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:

Источник

Древние знания

Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.

Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.

Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.

Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.

Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:

К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.

Утверждение теоремы

Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.

Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :

Теорема может быть применена к степеням любого бинома.

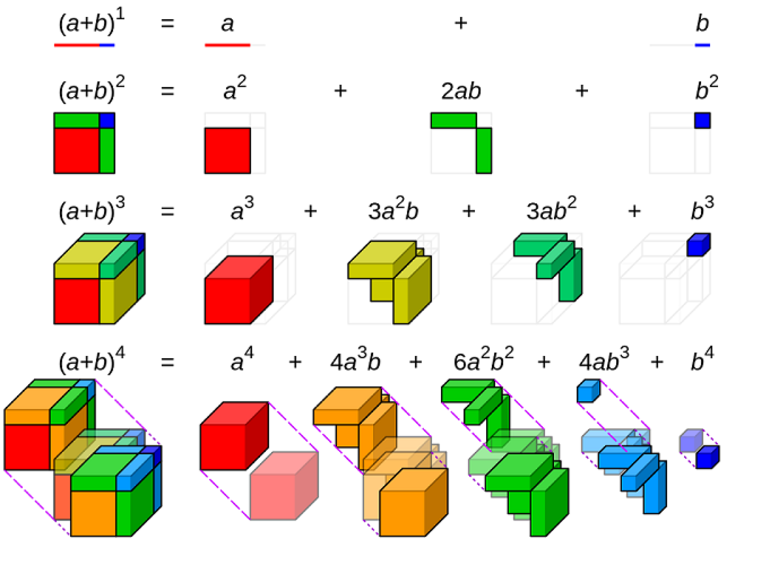
С точки зрения геометрии

Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.

Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:

Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.

Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.

Биномные обобщения

Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.

Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.

Короткий путь

Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.

Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).

Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.

Источник

Что такое обратный бином ньютона

План-конспект урока по математике:

« Бином Ньютона. Свойства биноминальных коэффициентов»

— обучающие : познакомить с формулой бинома Ньютона, научить применять формулу бинома Ньютона при возведении в степень двучлена;
— развивающие : способствовать развитию памяти, алгоритмического и логического мышления, внимания;
— воспитательные: продолжить воспитание чувства ответственности, самостоятельности, добросовестности.)

Оборудование : компьютер, мультимедийный проектор, экран, презентация, карточки с теоретическим материалом.

Тип урока – к омбинированный;

Формы работы учащихся – фронтальная, индивидуальная.

Сообщение темы, целей урока, практической значимости рассматриваемой темы.

2. Актуализация знаний

I . Фронтальный опрос:

1)Что изучает комбинаторика?

2)Какие виды соединений или выборок вам известны?

3) Отгадать кроссворд «Комбинаторика»

5!=….(120), А 5 2 =…(20)., С 4 2 =….(8)

Сколькими способами можно разместить 5 человек на скамейке?

3. Изложение нового материала: Работа с карточками теоретического материала. Заслушивание и анализ сообщений студентов. Написание конспекта.

I ) История комбинаторики ( Сообщение студента )

На прошлом уроке мы познакомились с основами комбинаторики. Домашнее задание для первой творческой группы было подготовить сообщение об истории возникновения комбинаторики как науки. (Сообщение студента)

Какие же ученые внесли вклад в развитие комбинаторики как науки?

Одним из выдающихся умов того времени был английский ученый Исаак Ньютон. Ваше домашнее задание было подготовить сообщение об этом великом гении.

II ) Исаак Ньютон- великий математик ( Сообщение студента )

Именно этому открытию мы посвятим наш сегодняшний урок. Запишем тему урока. Цели нашего урока : познакомиться с формулой бинома Ньютона, научиться применять формулу бинома Ньютона при возведении в степень двучлена.

Слово бином означает «Два числа» В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.

Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах

Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?

Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:

Возможно, вы уже догадались, что «рояль в кустах» – это треугольник Паскаля на предыдущей странице. Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1 ):

IV ) Блез Паскаль ( Сообщение студента )

Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона :

Таким образом можно записать формулу для возведения двучлена в любую степень. Давайте заметим некоторые свойства у слагаемых в разложении двучлена по формуле Бинома Ньютона.

V ) Свойства бинома Ньютона

Если в скобке знак минус, то знаки + и – чередуются.

Сумма степеней каждого слагаемого равна степени бинома.

VI ) Закрепление нового материала.

Мы знакомились с вами с применением бинома Ньютона при изучении формул сокращенного умножения: Где же ещё применяется Бином Ньютона?

VII ) Применение Бинома Ньютона.

В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:

Полученное произведение доказывает делимость исходного выражения на 16. Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница

VIII ) Что означает фразеологизм «Бином Ньютона»?

Подумаешь, Бином Ньютона

«Подумаешь, Бином Ньютона»
Кот промяукал Бегемот
(Он Воланда слуга покорный),
Предсказывая жизни ход.
Все это только подтверждает
Ньютона гений, но давно
Бином известен был в Китае,
Арабы знали про него.
Но обобщил Ньютон решение,
Возвёл он в степень многочлен.
Избавил нас от всех сомнений
Других же нет у нас проблем.
Скажите нам совсем без прений
Зачем нам нужен тот бином?
Комбинаторику явлений
Мы без бинома не найдём.
Nov. 7, 2015

Что нового вы узнали на уроке? Важна ли эта формула для математики? Трудно ли вам было усваивать новый материал?

Домашнее задание. Подготовка к контрольной работе.

( задание на листочках каждому студенту )

1. Из 12 членов команды нужно выбрать капитана и заместителя. Сколькими способами можно это сделать?

Выпускники экономического института работают в трех различных организациях: 17 человек в банке,23- в фирме и 19-в налоговой инспекции. Найдите вероятность того, что случайно встреченный выпускник работает в банке?

Имеется 8 различных книг 2 из которых сборники стихов. Сколькими способами можно расставить эти книги на полке так, чтобы справочники оказались рядом?

Для игры в КВН нужно выбрать команду из 6 человек, Сколькими способами можно это сделать, если в команде должно быть мальчиков и девочек поровну, и в классе 12 девочек и 10 мальчиков?

Сколько трехзначных чисел с разными цифрами можно составить из цифр, 0,1,3,6,7,9?

алгебраическая формула, открытая Ньютоном, выражающая какую угодно степень двучлена, а именно:

(х + а) n = х n + n/1(ax n-1) + (а 2 х n-2) + …(a n x n-m) + …

или, в компактной форме, пользуясь символом n! = 1.2.3…n:

(х + а) n = ∑ m (!x n-m a m

Формула эта была впервые дана Ньютоном в 1676 г. без доказательства. Она высечена на гробнице Ньютона, в Вестминстерском аббатстве, в Лондоне, хотя далеко не может считаться одним из важнейших открытий Ньютона.

Доказательство формулы Б. для целого показателя получается легко, как частный случай из более общей формулы, выражающей произведение произвольного числа двучленов. Легко убедиться непосредственным умножением, что для случая n = 2 или n = 3 имеет место формула:

(x + a 1)(х + а 2)…(х + а n) = х n + S n 1 x n-l + S n 2 x n-2 + … + S n n

(x + a 1)(x + a 2)…(x + a n-1) = х n-1 + (S n 1 + a n+1)x n + (S n 2 + S n 1 a n-1)x n-1 + … + S n n a n

и в то же время очевидно, что

S n 1 + a n+1 + 1 = S 1 n+1

S n 2 + S n 1 a n+1 = S 2 n+1

и т. д., так что правая часть последнего равенства есть

x n+1 + S 1 n+1 x n + S 2 n+1 х n-1 + … + (S n+1) n+1

и получим (х + а) n = x n + nax n-1 + (a 2 x n-2) + …

Таким образом верность формулы Ньютона для n целого, положительного доказана. Но уже и сам Ньютон показал, что она верна и для дробного, и для отрицательного. Приведем доказательство Эйлера для n какого угодно. Рассмотрим выражение:

f(n)f(–n) = f(0) = 1, т. е. f(–n) = 1/f(n) или

Большая Советская энциклопедия

Большой энциклопедический словарь

Этимологический словарь русского языка

Словарь крылатых слов и выражений

Толковый словарь Ожегова

Толковый словарь Ефремовой

Большой словарь русских поговорок

Словарь русского арго

«Бином Ньютона» в книгах

От Кеплера до Ньютона

1.2. От Анаксимандра до Ньютона

1.2. От Анаксимандра до Ньютона Существует широко распространенное убеждение, что на заре человечества первоначально было освоено понятие пространства и только потом, по подобию пространства, люди постепенно приспособили для практических целей понятие времени.Может

Мнение Р.Ньютона

Мнение Р.Ньютона В последнее время древние затмения были заново изучены Робертом Ньютоном, рассмотревшим не только античные, но и средневековые затмения. Мы не будем подробно излагать его труды, а приведем только одну цитату, подводящую итог его исследований.«Мы можем

Психология Ньютона

Психология Ньютона Всегда ли верны эти законы? Если мы рассмотрим нашу автомобильную аварию, то скажем да, мы знаем, что эти законы верны. Но верны ли они психологически? Многие сказали бы, что да. Например, третий закон можно было бы назвать законом оскорбления и возмездия:

Механика Ньютона

Механика Ньютона Теория тяготения Ньютона без использования его законов механики не была бы создана. Опуская детали, которые можно найти и в школьном учебнике физики, приведем эти три основных закона в окончательном виде. Без всякого сомнения, они имеют фундаментальное

Закон Ньютона

Закон Ньютона Закон всемирного тяготения после обсуждения в третьем чтении был отправлен на доработку… Фольклор Проверка закона Ньютона. Осмысление закона Ньютона до сих пор играет очень важную роль для осмысления представлений о гравитации вообще. Как можно

Законы Ньютона

Законы Ньютона К числу выдающихся научных достижений Ньютона относится высказанное им смелое предположение, по которому все материальные тела, кроме таких наглядных, очевидных свойств, как твердость, упругость, вес и т. д., имеют еще одно чрезвычайно важное свойство:

Бином

Дифференциальный бином

Ньютона бином

Подумаешь, бином Ньютона!

БИНОМ ХАЙЯМА

БИНОМ ХАЙЯМА

Это вам не бином Ньютона!

Это вам не бином Ньютона! Прежде чем гипотеза будет признана, необходимы неопровержимые доказательства. Парниковая гипотеза соответствовала данному условию, и именно поэтому в первом отчете МГЭИК вывод о существовании парникового эффекта выделен из сотен других

Бином Ньютона

Бином Ньютона Кубань стекает капельками с ледников Эльбруса, объединяется в отдельные безобидные ручейки, которые, сливаясь и принимая притоки Даут и Худес, образуют стиснутый горами необузданный поток. Перед самым городом скалы, словно устраивая последнюю проверку

Курьякова Татьяна Сергеевна

учитель математики МОУ «СОШ №36», г. Ангарск

Бином Ньютона – одна из тем, рассмотрение которых способствует глубинному пониманию учащимися на только комбинаторных понятий, но и формул сокращенного умножения. В данной статье представлен один из вариантов лекции для старшеклассников по теме «Бином Ньютона».

План лекции 1. Понятие бинома Ньютона

2. Свойства бинома и биномиальных коэффициентов

3. Типовые задачи по теме «Бином Ньютона»

4. Задачи, сводящиеся к использованию формулы бинома Ньютона (нестандартные задачи по теме «Бином Ньютона»)

1. Сборник конкурсных задач по математике для поступающих во втузы / Под ред. М.И.Сканави: Учеб. пособие. Санкт-Петербург, 1995. – с.84.

2. Супрун В.П. Избранные задачи повышенной сложности по математике. Мн.: Полымя, 1998. – 108с.

Понятие бинома Ньютона

Биномом Ньютона называют разложение вида:

Но, строго говоря, всю формулу нельзя назвать биномом, так как «бином» переводится как «двучлен». Кроме того, формула разложения была известна еще до Ньютона, Исаак Ньютон распространил это разложение на случай n

Цель изучения бинома Ньютона – упрощение вычислительных действий.

Компоненты формулы «бином Ньютона»:

Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.

Например, четвертая строчка треугольника как раз наглядно демонстрирует биномиальные коэффициенты для бинома четвертой степени:

Альтернатива треугольнику Паскаля:

перемножить почленно четыре скобки:

вспомнить разложение бинома Ньютона четвертой степени:

где Т – член разложения;
– порядковый номер члена разложения.

Свойства бинома и биномиальных коэффициентов

Сумма показателей степеней a и b :

Пусть
, тогда:

Тогда:

Типовые задачи по теме «Бином Ньютона»

К типовым (стандартным) заданиям по данной теме можно отнести задачи на вычисление, среди которых:

Найти член (номер члена) разложения бинома

Вывести бином по известным членам разложения (по известной сумме)

Вычислить сумму биномиальных коэффициентов разложения бинома

Продемонстрируем на примерах (их решение несложное, поэтому большинство предлагаем решить самостоятельно).

Разложить по формуле бином

ОБРАТИТЕ ВНИМАНИЕ на знакочередование!

Найти шестой член разложения

ОБРАТИТЕ ВНИМАНИЕ на знак!

Лучше начинать рассуждения со следующего:

Найдите два средних члена разложения

ОБРАТИТЕ ВНИМАНИЕ на то, что эти члены равноотстоят от конца, поэтому их биномиальные коэффициенты будут равны.

НЕ ЗАБУДЬТЕ в процессе решения проводить преобразования степеней с одинаковыми основаниями (то есть упрощать).

В биномиальном разложении
найти член разложения, не содержащий х

Ответ:

Задачи, сводящиеся к использованию формулы бинома Ньютона

(нестандартные задачи по теме «Бином Ньютона»)

К нестандартным заданиям по данной теме можно отнести такие, в которых нет явного намека на необходимость использования бинома. Однако в итоге, решение сводится к нему и выглядит очень интересным.

Доказать, что для любых
и для любых
верно неравенство Бернулли :

Пусть

Переформулируем требование: Доказать, что
, где

Так как
, значит в разложении как минимум три члена разложения, тогда:

Доказать, что

(Подсказка: используйте неравенство Бернулли)

Доказать, что при любом натуральном n число делится на 9

Начнем рассматривать бином в общем виде:

Осуществим замену:

Тогда уравнение перепишем:

Применим формулу бинома к левой части уравнения:

Константин Крылов один из интеллектуальных лидеров российских «новых правых». Последовательный русский националист, радикальный критик российской политическо

1. В каждом выражении на одно слагаемое больше, чем показатель степени n.

2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.

3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.

4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до «половины пути», а потом уменьшаются на те же значения обратно к 1.

Есть много особенностей в треугольнике. Найдите столько, сколько сможете.
Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b) 6 путем добавления следующей строки, используя особенности, которые мы нашли:

Мы видим, что в последней строке

Мы можем обобщить наши результаты следующим образом.

Бином Ньютона с использованием треугольника Паскаля

Разложение бинома используя значения факториала

Бином Ньютона с использованием обозначение факториала

Для любого бинома (a + b) и любого натурального числа n,
.

Бином Ньютона может быть доказан методом математической индукции. Она показывает почему называется биноминальным коэффициентом .

Нахождение определенного члена

Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.

Обратите внимание, что в биноме Ньютона дает нам 1-й член, дает нам 2-й член, дает нам 3-й член и так далее. Это может быть обощено следующим образом.

Нахождение (k + 1) члена

Общее число подмножеств

Полное число подмножеств

Пример 7 Сколько подмножеств имеет множество ?

Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно

. Таким образом, Венди может предложить 512 различных гамбургеров.

Источник