Физические величины.

Физической величиной называется физическое свойство материального объекта, процесса, физического явления, охарактеризованное количественно.

Значение физической величины выражается одним или несколькими числами, характеризующими эту физическую величину, с указанием единицы измерения.

Размером физической величины являются значения чисел, фигурирующих в значении физической величины.

Единицы измерения физических величин.

Единицей измерения физической величины является величина фиксированного размера, которой присвоено числовое значение, равное единице. Применяется для количественного выражения однородных с ней физических величин. Системой единиц физических величин называют совокупность основных и производных единиц, основанную на некоторой системе величин.

Широкое распространение получило всего лишь некоторое количество систем единиц. В большинстве случаев во многих странах пользуются метрической системой.

Основные единицы.

Измерить физическую величину – значит сравнить ее с другой такой же физической величиной, принятой за единицу.

Для каждой физической величины в системе единиц должна быть предусмотрена соответствующая единица измерения. Эталоном единицы измерения является ее физическая реализация.

Эталоном длины является метр – расстояние между двумя штрихами, нанесенными на стержне особой формы, изготовленном из сплава платины и иридия.

Эталоном времени служит продолжительность какого-либо правильно повторяющегося процесса, в качестве которого выбрано движение Земли вокруг Солнца: один оборот Земля совершает за год. Но за единицу времени принимают не год, а секунду.

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за 1 с совершает перемещение в 1 м.

Отдельная единица измерения используется для площади, объема, длины и т. д. Каждая единица определяется при выборе того или иного эталона. Но система единиц значительно удобнее, если в ней в качестве основных выбрано всего несколько единиц, а остальные определяются через основные. Например, если единицей длины является метр, то единицей площади будет квадратный метр, объема – кубический метр, скорости – метр в секунду и т. д.

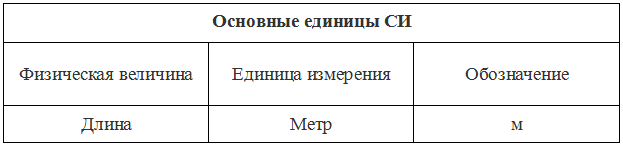
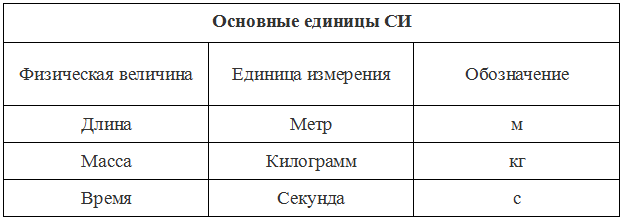
Основными единицами физических величин в Международной системе единиц (СИ) являются: метр (м), килограмм (кг), секунда (с), ампер (А), кельвин (К), кандела (кд) и моль (моль).

Источник

Единицы измерения

Этот урок не будет новым для новичков. Все мы слышали со школы такие понятия как сантиметр, метр, километр. А когда речь заходила о массе, обычно говорили грамм, килограмм, тонна.

Сантиметры, метры и километры; граммы, килограммы и тонны носят одно общее название — единицы измерения физических величин.

В данном уроке мы рассмотрим наиболее популярные единицы измерения, но не будем сильно углубляться в эту тему, поскольку единицы измерения уходят в область физики. Сегодня мы вынуждены изучить часть физики, поскольку нам это необходимо для дальнейшего изучения математики.

Единицы измерения длины

Для измерения длины предназначены следующие единицы измерения:

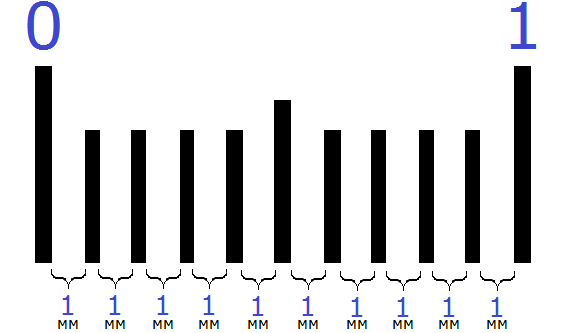
Самая маленькая единица измерения это миллиметр (мм). Миллиметры можно увидеть даже воочию, если взять линейку, которой мы пользовались в школе каждый день

Подряд идущие друг за другом маленькие линии это и есть миллиметры. Точнее, расстояние между этими линиями равно одному миллиметру (1 мм):

Следующая единица измерения это сантиметр (см). На линейке каждый сантиметр обозначен числом. К примеру наша линейка, которая была на первом рисунке, имела длину 15 сантиметров. Последний сантиметр на этой линейке выделен числом 15.

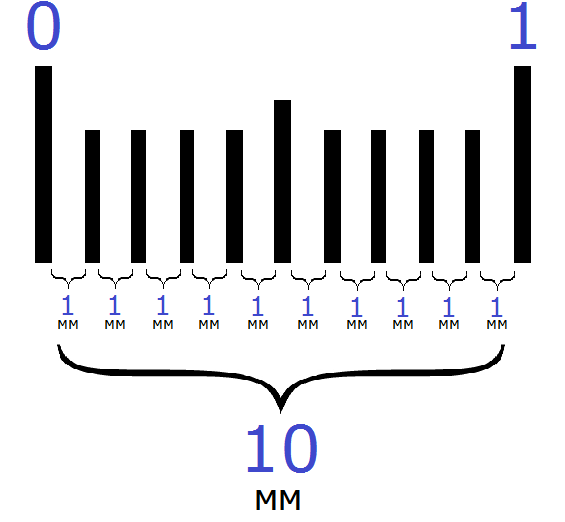
В одном сантиметре 10 миллиметров. Между одним сантиметром и десятью миллиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 см = 10 мм

Вы можете сами убедиться в этом, если посчитаете количество миллиметров на предыдущем рисунке. Вы обнаружите, что количество миллиметров (расстояний между линиями) равно 10.

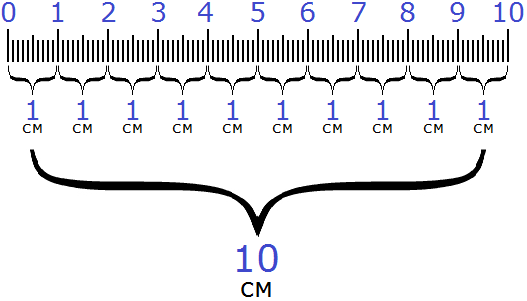
Следующая единица измерения длины это дециметр (дм). В одном дециметре десять сантиметров. Между одним дециметром и десятью сантиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 дм = 10 см

Вы можете убедиться в этом, если посчитаете количество сантиметров на следующем рисунке:

Вы обнаружите, что количество сантиметров равно 10.

Следующая единица измерения это метр (м). В одном метре десять дециметров. Между одним метром и десятью дециметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 м = 10 дм

К сожалению, метр нельзя проиллюстрировать на рисунке, потому что он достаточно великоват. Если вы хотите увидеть метр в живую, возьмите рулетку. Она есть у каждого в доме. На рулетке один метр будет обозначен как 100 см. Это потому что в одном метре десять дециметров, а в десяти дециметрах сто сантиметров:

1 м = 10 дм = 100 см

100 получается путём перевода одного метра в сантиметры. Это отдельная тема, которую мы рассмотрим чуть позже. А пока перейдём к следующей единице измерения длины, которая называется километр.

Километр считается самой большой единицей измерения длины. Есть конечно и другие более старшие единицы, такие как мегаметр, гигаметр тераметр, но мы не будем их рассматривать, поскольку для дальнейшего изучения математики нам достаточно и километра.

В одном километре тысяча метров. Между одним километром и тысячью метрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 км = 1000 м

В километрах измеряются расстояния между городами и странами. К примеру, расстояние от Москвы до Санкт-Петербурга около 714 километров.

Международная система единиц СИ

Международная система единиц СИ — это некоторый набор общепринятых физических величин.

Основное предназначение международной системы единиц СИ — достижение договоренностей между странами.

Мы знаем, что языки и традиции стран мира различны. С этим ничего не поделать. Но законы математики и физики одинаково работают везде. Если в одной стране «дважды два будет четыре», то и в другой стране «дважды два будет четыре».

Основная проблема заключалась в том, что для каждой физической величины существует несколько единиц измерения. К примеру, мы сейчас узнали, что для измерения длины существуют миллиметры, сантиметры, дециметры, метры и километры. Если несколько ученых, говорящих на разных языках, соберутся в одном месте для решения какой-нибудь задачи, то такое большое многообразие единиц измерения длины может породить между этими учеными противоречия.

Один ученый будет заявлять, что в их стране длина измеряется в метрах. Второй может сказать, что в их стране длина измеряется в километрах. Третий может предложить свою единицу измерения.

Поэтому была создана международная система единиц СИ. СИ это аббревиатура от французского словосочетания Le Système International d’Unités, SI (что в переводе на русский означает — международная система единиц СИ).

В СИ приведены наиболее популярные физические величины и для каждой из них определена своя общепринятая единица измерения. К примеру, во всех странах при решении задач условились, что длину будут измерять в метрах. Поэтому, при решении задач, если длина дана в другой единице измерения (например, в километрах), то её обязательно нужно перевести в метры. О том, как переводить одну единицу измерения в другую, мы поговорим немного позже. А пока нарисуем свою международную систему единиц СИ.

Наш рисунок будет представлять собой таблицу физических величин. Каждую изученную физическую величину мы будем включать в нашу таблицу и указывать ту единицу измерения, которая принята во всех странах. Сейчас мы изучили единицы измерения длины и узнали, что в системе СИ для измерения длины определены метры. Значит наша таблица будет выглядеть так:

Единицы измерения массы

Вместе с тем, масса и вес это разные понятия. Вес — это сила с которой тело действует на горизонтальную опору. Вес измеряется в ньютонах. А масса это величина, показывающая количество вещества в этом теле.

Для измерения массы используются следующие единицы измерения:

Самая маленькая единица измерения это миллиграмм (мг). Миллиграмм скорее всего вы никогда не примените на практике. Их применяют химики и другие ученые, которые работают с мелкими веществами. Для вас достаточно знать, что такая единица измерения массы существует.

Следующая единица измерения это грамм (г). В граммах принято измерять количество того или иного продукта при составлении рецепта.

В одном грамме тысяча миллиграммов. Между одним граммом и тысячью миллиграммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 г = 1000 мг

Следующая единица измерения это килограмм (кг). Килограмм это общепринятая единица измерения. В ней измеряется всё что угодно. Килограмм включен в систему СИ. Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «масса»:

В одном килограмме тысяча граммов. Между одним килограммом и тысячью граммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 кг = 1000 г

Следующая единица измерения это центнер (ц). В центнерах удобно измерять массу урожая, собранного с небольшого участка или массу какого-нибудь груза.

В одном центнере сто килограммов. Между одним центнером и ста килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 ц = 100 кг

Следующая единица измерения это тонна (т). В тоннах обычно измеряются большие грузы и массы больших тел. Например, масса космического корабля или автомобиля.

В одной тонне тысяча килограмм. Между одной тонной и тысячью килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 т = 1000 кг

Единицы измерения времени

Что такое время думаем объяснять не нужно. Каждый знает что из себя представляет время и зачем оно нужно. Если мы откроем дискуссию на то, что такое время и попытаемся дать ему определение, то начнем углубляться в философию, а это нам сейчас не нужно. Лучше начнём с единиц измерения времени.

Для измерения времени предназначены следующие единицы измерения:

Самая маленькая единица измерения это секунда (с). Есть конечно и более маленькие единицы такие как миллисекунды, микросекунды, наносекунды, но их мы рассматривать не будем, поскольку на данный момент в этом нет смысла.

В секундах измеряются различные показатели. Например, за сколько секунд спортсмен пробежит 100 метров. Секунда включена в международную систему единиц СИ для измерения времени и обозначается как «с». Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «время»:

Следующая единица измерения времени это минута (м). В одной минуте 60 секунд. Между одной минутой и шестьюдесятью секундами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 м = 60 с

Следующая единица измерения это час (ч). В одном часе 60 минут. Между одним часом и шестьюдесятью минутами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 ч = 60 м

Следующая единица измерения времени это сутки. В сутках 24 часа. Между одними сутками и двадцатью четырьмя часами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 сут = 24 ч

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Измерение. Шкалы измерений

Известное изречение гласит «все познается в сравнении».

Для идентификации объектов и их характеристик во множестве их проявлений требуется большое количество и разнообразие мер. С учетом особенностей измеряемых объектов и задач измерений меры группируют и используют для построения шкал измерений.

Шкала измерений – упорядоченное множество проявлений количественных или качественных характеристик объектов, а также самих объектов. Указанное множество может быть образовано из наименований и обозначений (в том числе в цифровой форме) объектов и их характеристик, а также из значений и числовых значений (для количественных характеристик).

Согласно РМГ 83-2007 [7] «шкала измерений – отображение множества различных проявлений количественного или качественного свойства на принятое по соглашению упорядоченное множество чисел или другую систему логически связанных знаков (обозначений)». «Измерение – сравнение конкретного проявления измеряемого свойства (величины) со шкалой измерений этого свойства (величины) в целях получения результата измерений (оценки свойства или значения величины)».

Под качественной характеристикой в определении шкалы измерений и далее понимается описание объектов, их свойств и состояний, в словесной форме, в том числе с использованием наименований и обозначений.
Количественная характеристика – характеристика, которая может быть представлена числовым значением, равным отношению количественного содержания этой характеристики к еѐ базовой реализации, называемой единицей измерения.

Шкала наименований – шкала, состоящая из множества наименований (обозначений) объектов или проявлений их характеристик, в соответствии которым поставлено описание объекта (конкретная реализация объекта, его графическое изображение, математическая формула, график и т.п.) или проявлений его характеристик.

Наименование (обозначение) в этом случае рассматривают как обобщенную характеристику объекта или его свойств и состояний. С помощью шкалы наименований устанавливают эквивалентность (равноценность) измеряемого объекта или его характеристик и описания, поставленному в соответствие тому или иному наименованию (обозначению). Это позволяет отнести объект к какой-либо группе или выделить его, путем присвоения индивидуального наименования (обозначения), после чего наименования (обозначения) применяются как идентификаторы объектов (характеристик объектов). При построении шкал наименований могут использоваться числа, но лишь как метки объектов. Примерами таких шкал являются: атласы цветов (до 1000 наименований), запахов (сырой, затхлый, кислый и т.д.), вкуса (чистый, полный, гармоничный и т.д.); множество номеров телефонов, автомашин, паспортов; разделение людей по полу, расе, национальности; классификаторы промышленной продукции, специальностей высшего образования; терминологические справочники и т.п.

Числа, знаки, обозначения, наименования, составляющие шкалу наименований, разрешается менять местами. Для результатов измерений, полученных с использованием этой шкалы, нет отношений типа «больше — меньше», не применимы понятия единица измерения, нуль, размерность. С ними могут проводиться только некоторые математические операции. Например, числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.

Оценки экспертов часто осуществляются с использованием шкал порядка. Типичным примером являются задачи ранжирования и классификации промышленных объектов, подлежащих экологическому страхованию.
В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше — меньше», «лучше — хуже» и т.п. Однако нельзя утверждать, что землетрясение в 2 балла (лампа качнулась под потолком) ровно в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего на поверхности земли).
Шкалы наименований и порядка, для которых не определены единицы измерений, называют также условными шкалами или не метрическими шкалами.

Абсолютная шкала – шкала числовых значений количественной характеристики. Отличительные признаки абсолютных шкал: наличие естественного нуля и отсутствие необходимости в единице измерений. С использованием абсолютных шкал измеряют коэффициенты усиления, ослабления, амплитудной модуляции, нелинейных искажений, отражения, коэффициент полезного действия и т. п. Результаты измерений в абсолютных шкалах при необходимости выражают в процентах, промилле, байтах, битах, децибелах.
Разновидностью абсолютных шкал являются дискретные (счетные) шкалы, в которых результат измерения выражается числом частиц, квантов, или других объектов, эквивалентных по проявлению измеряемого свойства. Например, шкалы для электрического заряда ядер атомов, числа квантов (в фотохимии), количества информации. Иногда за единицу измерений (со специальным названием) в таких шкалах принимают какое-то определенное число частиц (квантов), например один моль – число частиц, равное числу Авогадро.
Абсолютная шкала, диапазон значений которой находится в пределах от нуля до единицы (или некоторого предельного значения по спецификации шкалы) называют абсолютной ограниченной шкалой.

Шкалы разностей (интервалов), отношений и абсолютные классифицируют как метрические или физические шкалы. Эти шкалы допускают логарифмическое преобразование, часто применяемое на практике, что приводит к изменению типа шкал. Такие шкалы называют логарифмическими. Практическое распространение получили логарифмические шкалы на основе применения систем десятичных и натуральных логарифмов, а также логарифмов с основанием два.

Практически реализация шкал измерений достигается путем стандартизации как самих шкал и единиц измерений, так и, при необходимости, способов и условий (спецификаций) их однозначного воспроизведения.
Измерение с помощью шкал заключается в установлении соответствия объекта или его характеристики отметке на шкале измерений. После чего объекту измерений приписывают количественную или качественную определенность, соответствующую выявленной отметке шкалы.

Источник

О размерностях физических величин

О термине «физическая размерность»

Термин “размерность” имеет совершенно разные значения в математике (геометрии) и физике. В математике размерность некоторой количественной меры (величины, параметра, переменной, константы и пр.) есть также количественная мера, определяющая степень, в которую возводится некая первичная по отношению к определяемой величины мера, в отношении которой (первичной меры) определяется размерность. То есть

В физике формальное определение размерности дано в советском ГОСТ 16263-70 (ГСИ. Метрология. Термины и определения), который действует в России и Казахстане и в настоящее время:

В БСЭ имеется другое, неверное определение размерности:

[авт.: Коган Б. Ю., то же: Коган Б. Ю., Размерность физической величины, М., Изд-во «Наука», 1967, 72с. с илл., 100000 экз.]

Это определение не соответствует ни стандарту, ни смыслу понятия физической размерности. Кроме того, размерность физической величины и единица измерений физической величины синонимами не являются.

В Международной системе величин (англ. International System of Quantities, ISQ), на которой базируется Международная система единиц (СИ), в качестве основных величин выбраны длина, масса, время, электрический ток, термодинамическая температура, сила света и количество вещества. Символы их размерностей в СИ приведены в таблице[1].

Таблица 1. Основные физические размерности в СИ

Символ для размерности

Количество вещества

Для обозначения производных физических размерностей используют символ dim, а также сочетание размерностей в конкретной системе единиц, например, СИ, заключенные в квадратные скобки.

Например, для скорости при равномерном движении выполняется

Аналогично для размерности ускорения получается

Из уравнения второго закона динамики с учётом размерности ускорения для размерности силы следует:

В общем случае размерность физической величины представляет собой произведение размерностей основных величин, возведённых в различные (положительные или отрицательные, целые или дробные) степени n i

dim X = L n1 M n2 T n3 I n4 Θ n5 M n6 J n7

Показатели степеней n i в этом выражении называют показателями размерности физической величины. Если в физической размерности величины хотя бы один из показателей размерности не равен нулю, то такую величину называют имеющей физическую размерность (качество), а значит, эта величина является реально физической. Если все показатели размерности равны нулю, то рассматриваемая величина есть всего лишь математический коэффициент, количественное соотношение каких-то двух величин, но не реальная физическая величина.

Коррекция размерностей системы СИ в реальной физике

Хотя система СИ наиболее физична из всех используемых систем физических единиц измерений (СГС, СГСЭ и пр.), но на самом деле она не является ни оптимальной, ни даже корректной в отношении физических размерностей. И вот почему.

Основные физические размерности должны быть неразложимы на составные размерности. В СИ это не так. Размерность силы электрического тока является комбинацией размерности заряда и размерности времени

Размерность температуры представляет собой производную размерность от размерности энергии и размерности энтропии

Точно так же обстоит дело с силой света, размерность которой есть сложносоставная величина.

Для исключения нелогичностей и успешности размерностного анализа в реальной физике необходимо использовать систему основных размерностей, показанную в таблице 2.

Таблица 2. Основные физические размерности в реальной физике

Символ для размерности

Электрический заряд

Здесь в основные размерности входит угол, так как наличие размерности угла коренным образом меняет смысл физической величины, что часто не учитывается в СИ.

К примеру, размерность момента силы в СИ равна размерности энергии [N·m] = [J], что есть нонсенс. В реальности в размерность момента силы входит угол [N·m/rad], что соответствует смыслу этой физической величины, ибо [N·m/rad] означает, что указанное в величине количество энергии приходится на каждый радиан.

Без правильного учета размерности энтропии невозможно проводить анализ реальных термодинамических и информационных явлений в физике.

С помощью произведения основных физических размерностей может быть получена размерность любой физической величины

dim X = T n1 A n2 L n3 M n4 C n5 E n6

Системы единиц измерения физических величин

Наиболее рациональной для применения в физике видится система СИ, которая применяется в качестве стандарта во многих странах и наиболее точно соответствует физической сущности величин. Именно она с некоторыми корректировками используется в реальной физике.

В СИ размерность любой физической величины записывают, как произведение символов, которыми именуются физические размерности, каждый из которых возведён в рациональную степень.

Например, размерность скорости — расстояние, делённое на время [m/s], а размерность силы — масса, умноженная на расстояние и делённая на время в квадрате [kg·m/s 2 ]. Выражение размерности для вычисляемой величины (количества) записывается в квадратных скобках.

В механике размерность любой величины может быть выражена через расстояние [m], массу [kg] и время [s]. Электрические и магнитные величины также могут быть выражены через эти три размерности плюс размерность электрического заряда в Кулонах [C]. Для рассмотрения существа физического процесса (его реального качества) часто удобнее использовать составные, то есть производные от базовых, размерности, такие, как размерность электрического тока [a] = [C/s], силы [N] = [kg·m/s 2 ], энергии [J] = [kg·m 2 /s 2 ] и пр.

Любая физическая величина имеет физическую размерность как атрибут ее качества, если у какой-либо величины нет физической размерности (говорят, что она «безразмерна»), то это не физическая величина, а только некий относительный математический коэффициент, отношение между двумя другими физическими величинами одной и той же размерности.

К сожалению, последнего не понимают многие математики («физико-математики»). Они пытаются присвоить смысл самостоятельной физической величины таким коэффициентам или даже построить целые безразмерные «физико-математические» системы единиц, не понимая, что без качества физической размерности такие системы сами не имеют физического качества, но являются лишь количественно-математическими моделями, толерантными к логическим ошибкам. То есть такие математические модели допускают нарушение логики в результате подмены одного физического качества другим, просто не видя физического качества.

К таким системам относятся релятивистский вариант системы СГСЭ, релятивистская система безразмерных единиц (которую не следует путать с системой естественных единиц Макса Планка), система MLT, и прочие разновидности систем, пытающихся выбросить из физики ее физическое качество, то есть содержание, и сделать физику разделом математики. К примеру, в системе MLT (масса-длина-время) исключены другие физические качетва, отнюдь не сводимые к массе, длине и времени. Среди них углы (плоские и телесные) и электрический заряд.

Основные физические размерности и единицы измерений в СИ приведены в таблице.

Физические размерности в Международной системе единиц (СИ)

tсекундасs

Угловые единицы

Плоский угол

αрадианрадrad1 coil = 1 cycle = 2 π radТелесный угол

θстерадианстрадstradstrad = rad 2Циклическая частота, скорость вращения

εрад/с 2rad/s 2

Пространственные единицы

Расстояние

lметрмmПлощадь

Sкв. метрм 2m 2Объём

Vкуб. метрм 3m 3Линейная скорость

vм/сm/sЛинейное ускорение

aм/с 2m/s 2Радиус, дуга

rм/радm/radКинематическая вязкость, циркуляция скорости

νм 2 /сm 2 /sКинетический потенциал

φм 2 /с 2m 2 /s 2J/kgДебит, объемная скорость, объемный расход

dбернуллим 3 /сm 3 /sОбъемное ускорение, гравитационный параметр

μкеплерм 3 /с 2m 3 /s 2

Механические единицы

Масса, линейная инерция

mкилограммкгkg1kg = 1000gМеханический импульс, количество движения

pбраункг·м/сkg·m/skg·m/sСила

FньютонНNkg·m/s 2Момент импульса, кинетический момент,
момент количества движения

Kkg·m 2 /(s·rad)Кинетическая энергия вращательного движения

Tkg·m 2 /s 2Момент силы

Mkg·m 2 /(s 2 ·rad), J/radДавление

PпаскальПаPakg/(m·s 2 ), PaДинамическая вязкость

η10 пуазПа·сPa·skg/(m·s), Pa·sАкустическое волновое сопротивление, удельный импеданс среды

Z_aакустический омакОмacOhmkg/(s·m 2 )Акустический импеданс, объемный импеданс среды

z_aакОм/м 2acOhm/m 2kg/(s·m 4 )Механический импеданс, механическое активное и реактивное сопротивление, массовый расход

Z_mмеханический оммехОмmechOhmkg/sМомент инерции

JгалилейГGkg·m 2 /rad 2Работа, механическая энергия

WджоульДжJkg·m 2 /s 2Механическая мощность

PваттВтWkg·m 2 /s 3Температура

T°KДж/нитJ/nitkg·m 2 /(s 2 ·нит)

Электрические единицы

Электрический заряд, электрический поток

qкулонКлCC, a·sЭлектрический момент

M_eC·mC·m/radЭлектрическая индукция

DC/m 2Вектор поляризации

PC/m 2Электрическое напряжение, электрический потенциал

UвольтВVkg·m 2 /(s 2 ·C), J/CНапряжённость потенциального электрического поля

Eвольт/метрВ/мV/mkg·m/(s 2 ·C)Напряжённость вихревого электрического поля

εвольт/витокВ/витV/coilkg·m/(s 2 ·C·coil)Электрическая ёмкость

CфарадаФFC/V, s/Ω, C 2 /J, C 2· s 2 /m 2 ·kgАбсолютная диэлектрическая проницаемость

ε_aэпсилонF/mC 2 ·s 2 /m 3 ·kgАбсолютная диэлектрическая восприимчивость

κ_aкаппаF/mC 2 ·s 2 /m 3 ·kgЭлектрический ток

IамперАaC/s,Электрическое сопротивление цепи

Xом/оборотОм/оборотΩ/cycleJ/(a·C·cycle), W/(a 2 ·cycle) Удельное электрическое сопротивление

ρом·мОм·мΩ·mЭлектропроводность, электрическая проводимость

σсимменс/метрСм/м1/(Ωm)Электрическая энергия

PваттВтWJ/s, V·C/s, V·a, V 2 /Ω, Ω·a 2Реактивная электрическая мощность

Qвар (вольт-ампер реактивные)ВАрVARJ/s, V·C/s, V·a, V 2 /Ω, Ω·a 2

Магнитные единицы

Магнитный поток

ФвеберВбWbJ/(a·cycle), V·s/cycle Магнитная индукция

LгенриГнHn, Ω·s/radkg·m 2 /(s 2 ·a 2 ·rad), J/(a 2 ·rad), Wb/a Абсолютная магнитная проницаемость

R mампер-виток/вебер1/Гн1/HnC 2 /(kg·m 2 ), 1/Hn

Печально, что составители российских метрологических нормативных документов запретили использование термина «системы единиц измерения физических величин», разрешая использование лишь термина «системы единиц физических величин», не понимая, что любая единица физической величины имеет смысл только в процессе физических измерений и для него. Любая метрологическая информация поступает к нам (в измерительный прибор) только в процессе измерения, а само измерение возможно лишь при использовании единиц измерения.

Проверка физической размерности

В формулах, имеющих физический смысл, только величины, имеющие одинаковую размерность, могут складываться, вычитаться или сравниваться. Например, сложение массы какого-либо предмета с длиной другого предмета не имеет смысла. Также невозможно сказать, что больше: 1 килограмм или 3 секунды. Из этого правила, в частности, следует, что левые и правые части всех физических уравнений должны иметь одинаковую размерность.

Эти правила используются для проверки правильности физических формул. Если в полученном уравнении какое-то из них нарушается, то ясно, что, в качественной модели анализируемого физического процесса была допущена ошибка, которая делает бессмысленными результаты всех количественных (математических) операций.

Анализ физических размерностей

Для исключения нарушения логики качественно-логический анализ всегда должен предшествовать количественному, ибо он является анализом более высокого иерархического уровня, нежели количественно-математический.

Для проведения качественно-логического анализа составляют уравнения размерностей, которые составляют путем замены физических величин (параметров) обозначением их физических размерностей. При этом левая и правая часть уравнения после приведения к подобным размерностям должны иметь эквивалентные размерности.

Пример анализа физической размерности

Физическое уравнение: F = m·a

Уравнение размерностей до приведения: [N] = [kg·m/s 2 ]

Уравнение размерностей после приведения: [kg·m/s 2 ] = [kg·m/s 2 ]

При этом множество формул, описывающих данную систему или процесс, сужается до узкого перечислимого множества вариантов (с точностью до безразмерной константы). Суть метода заключается в том, что из параметров, характеризующих систему, составляется выражение, имеющее нужную размерность. При этом нельзя забывать, что это лишь метод подгонки, единственность решения которого еще предстоит доказать.

Как уже было отмечено, при анализе размерностей формул размерность левой части уравнения должна быть равна размерности правой части уравнения. Отсутствие такого равенства говорит о неверности формулы. Однако наличие такого равенства не является достаточным условием справедливости выводимой формулы.

Степени физических размерностей

В выражениях размерности часто встречается некоторая степень, то есть физическая размерность [x] может быть какой-то степени n : x n :

При этом n может быть не только целым числом, но и дробным:

Появление дробной степени в физической размерности соответственно означает, что физическая величина, имеющая такую дробную размерность проявляет свойство аддитивности (меры) по отношению базовой физической размерности именно в этой дробной степени. Примером могут служить различные спектральные меры, являющиеся функцией частоты или энергии в дробной степени, например [Hz 1/2 ] или [J 1/2 ], когда аддитивной мерой от частоты в первой степени является энергия сигнала, а используется выражение для амплитуды или нормы сигнала (см. «Энергетические спектры сигналов»). То же самое относится к физическим мерам, аддитивным к объемам. В них может быть размерность [m 1/3 ].

«Безразмерные» физические величины

В отличие от спекулятивно-математической физики, пытающейся отказаться от физических размерностей для формального замыкания теоретической физики на математическую релятивистскую модель, в реальной физике кроме физических величин, характеризуемых физическим качеством, существуют и величины, характеризующие чисто количественные отношения между физическими величинами. Именно их можно считать «безразмерными», но реально имеющими, как минимум, количественно-математическое качество, обычно [раз, доля, %, дБ], проявляющееся при делении величин физического качества одной и той же физической размерности. В таблице ниже приведены некоторые «безразмерные» величины, используемые в физике. Как правило, они называются коэффициентами.

Источник