Баллистический коэффициент что это
Что такое баллистический коэффициент
Баллистический коэффициент является одной из важнейших характеристик пули! Зная БК пули, ее массу и начальную скорость можно рассчитать траекторию полета пули и ввести необходимые поправки в прицел, чтобы попасть в цель даже на такой дистанции, на которую он не был пристрелян. Пули с большим БК лучше сохраняют скорость, имея меньшее сопротивление воздуха и поэтому имеют более пологую траекторию.
Часто покупатели спрашивают, какие пули для пневматики лучше купить, ответ на этот вопрос зависит от того, для каких целей приобретаются пули. Если речь идет о стрельбе по мишеням на расстоянии 10-25 метров, то тогда можно покупать стандартные матчевые пули с плоской головной частью, например H&N excite Econ или H&N Finale Match. Эти пули имеют невысокий БК и предназначены для стрельбы по бумажным мишеням на небольшие расстояния. Их основная особенность «вырезать» на мишени точные отверстия в месте попадания. Если же пули приобретаются для охоты то в этом случае необходимо выбирать пули исходя из дистанции на которой в основном собираетесь охотится.
В нашем магазине вы можете приобрести пули известного немецкого производителя Haendler&Natermann Sport GmbH.
Чтобы нагляднее показать, как баллистический коэффициент влияет на траекторию пули, и на остаточную энергию пули у цели, были произведены расчеты в баллистическом калькуляторе для четырех видов пуль калибра 5.5 мм. с разным БК и разной массой. Расчеты производились для винтовки мощностью 41 Дж. пристрелянной на дистанцию 50 метров, при условии что фактически выстрел будет производится на дистанцию 100 м. Также мы оценим, как воздействует ветер на эти пули, на дистанции 100 м.
Baracuda Power это омеднённая пуля имеющая следующие хар-ки:
Mасса = 1.37 г. ; БК = 0.044
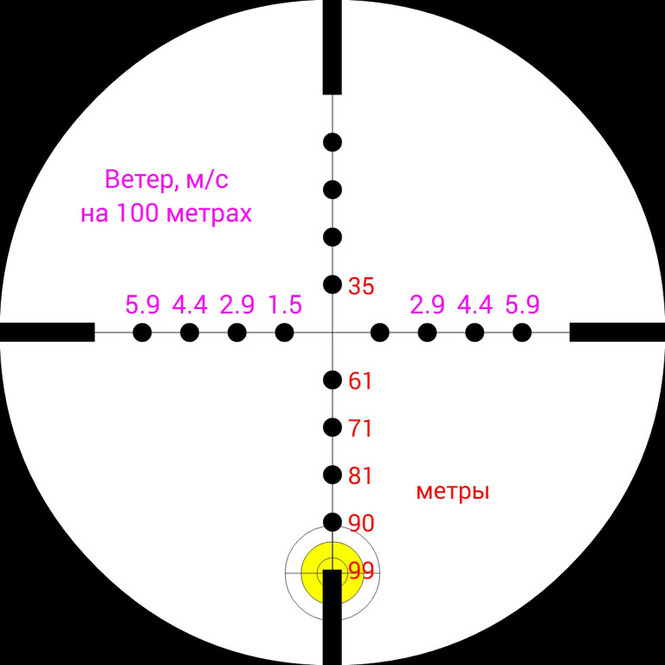
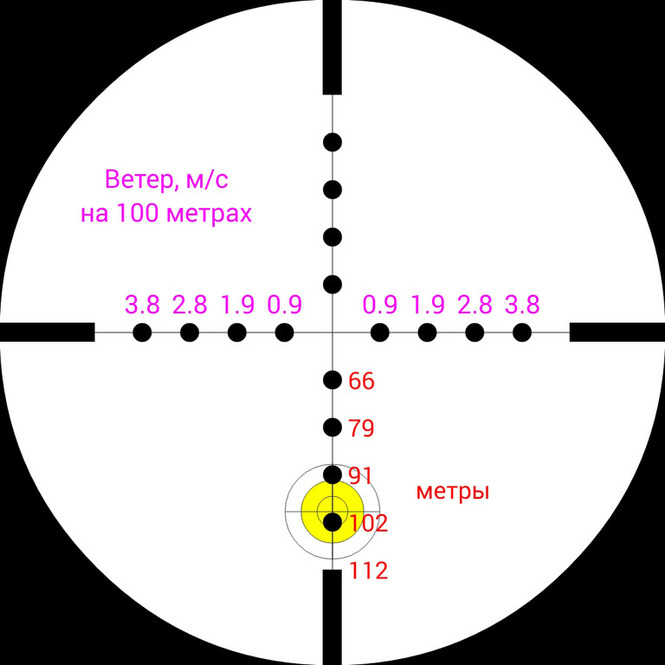
При выстреле из винтовки мощностью 41Дж эта пуля будет лететь со скоростью 245 м/c, на дистанции 100 метров она будет иметь остаточную скорость 183м/c и энергию 23Дж.
Понижение траектории на этой дистанции составит 50 см., а время полета до цели 0.48с.
Боковой снос пули при условии ветра в 2 м/c составит 14 см.
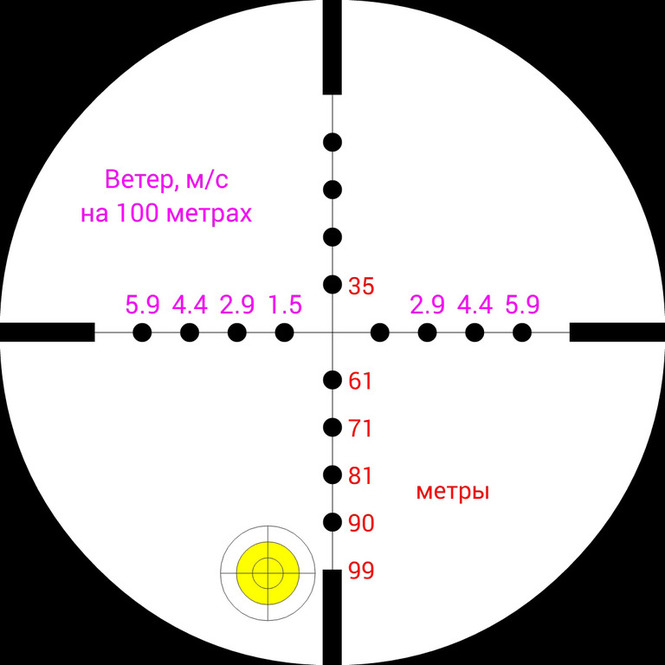
На этих изображениях показано, куда необходимо целится, чтобы попасть пулей Baracuda Power в цель на дистанции 100 м., при условии, что изначально винтовка пристреляна на 50м. Также на правом изображении показано, как повлияет ветер со скоростью 2м/c на этой дистанции.
Rabbit Magnum это тяжелая охотничья пуля с хар-ми:
Mасса = 1.65 г. ; БК = 0.036
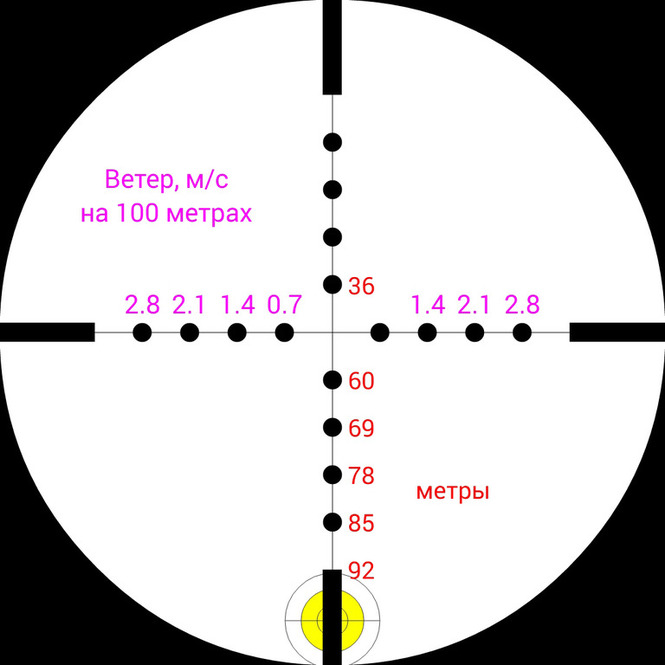
При выстреле из винтовки мощностью 41Дж эта пуля полетит со скоростью 222 м/c, на дистанции 100 метров она будет иметь остаточную скорость 155м/с и энергию 20Дж.
Понижение траектории на этой дистанции составит 66 см., а время полета до цели 0.55с.
Боковой снос пули при условии ветра в 2 м/c составит 18 см.
На этих изображениях показано, куда необходимо целится, чтобы попасть пулей Rabbit Magnum в цель на дистанции 100 м, при условии, что изначально винтовка пристреляна на 50м. Также на правом изображении показано, как повлияет ветер со скоростью 2 м/c на этой дистанции.
Baracuda Green это легкая пуля из оловянного сплава без содержания свинца, ее хар-ки:
Mасса = 0.8 г. ; БК = 0.029
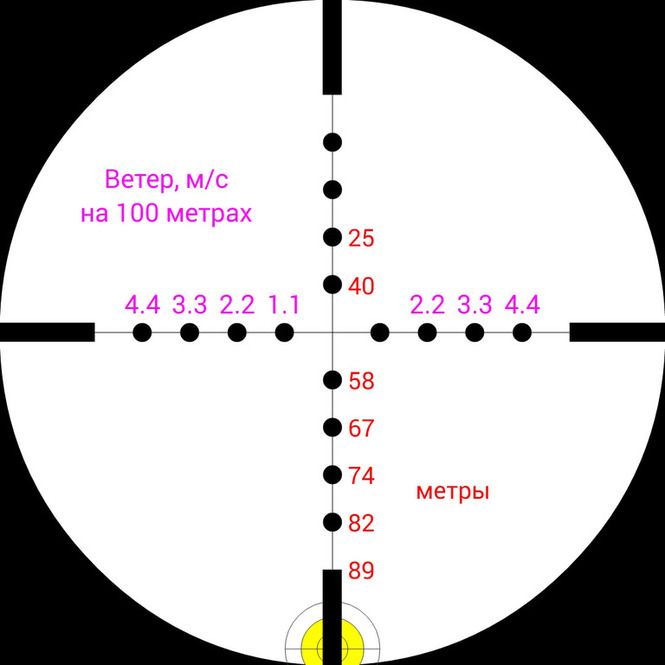
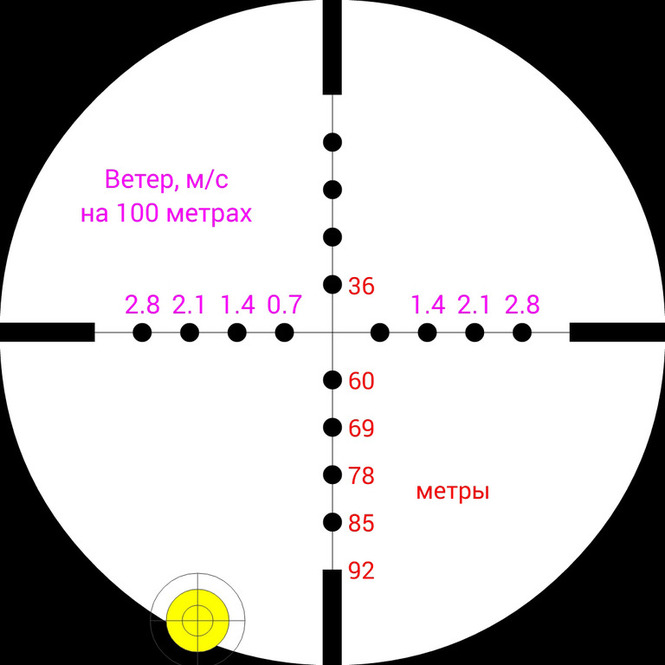
При выстреле из винтовки мощностью 41 Дж эта пуля полетит со скоростью 320 м/c, на дистанции 100м она будет иметь остаточную скорость 191 м/с и энергию 15Дж.
Понижение траектории на этой дистанции составит 38см, а время полета до цели 0.42с.
Боковой снос пули при условии ветра в 2 м/c составит 21 см.
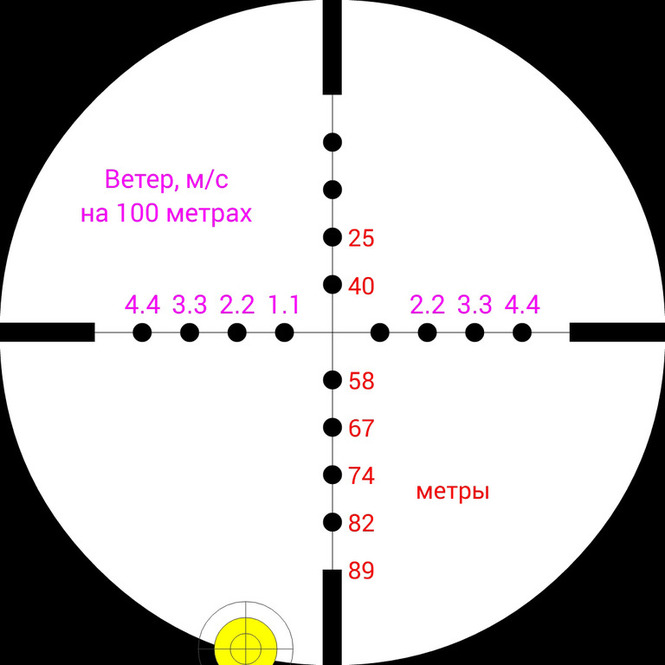
На этих изображениях показано куда необходимо целится, чтобы попасть пулей Baracuda Green в цель на дистанции 100 м, при условии, что изначально винтовка пристреляна на 50м. Также на правом изображении показано, как повлияет ветер со скоростью 2м/c на этой дистанции.
Crow Magnum это экспансивная, охотничья пуля, предназначенная для охоты на небольших и средних дистанциях, ее хар-ки:
Mасса = 1.18 г. ; БК = 0.022
При выстреле из винтовки мощностью 41Дж эта пуля полетит со скоростью 265 м/c,
на дистанции 100 м. она будет иметь остаточную скорость 147 м/с и энергию 13 Дж.
Понижение траектории на этой дистанции составит 60 см, а время полета до цели 0.52с.
Боковой снос пули при условии ветра в 2 м/c составит 28 см.
На этих изображениях показано куда необходимо целится, чтобы попасть пулей Crow Magnum в цель на дистанции 100м, при условии, что изначально винтовка пристреляна на 50м. Также на правом изображении показано, как повлияет ветер со скоростью 2м/c на этой дистанции.
Итак, мы видим, что наибольшую остаточную энергию у цели, имеют пули с наибольшим
Пули же с меньшим БК и массой – это Baracuda Green и Crow Magnum имеют остаточную энергию в 15 и 13Дж соответственно.
Для примера, для надежного поражения зайца необходима энергия 40-50 Дж, утки 12-18 Дж, рябчика 4-5 Дж, тетерева 15-20 Дж.
Ветровому сносу менее подвержены также пули, имеющие наибольший БК и массу –
Baracuda Power и Rabbit Magnum – 14 и 18 см соответственно, при ветре 2 м/с на дистанции 100 м.
Пули Baracuda Green и Crow Magnum имеют ветровой снос в 21 и 28 см соответственно.
Теперь вы узнали, как влияют на траекторию пули ее масса и баллистический коэффициент, также на траекторию пули влияют температура воздуха и его давление, и при расчете необходимо вносить эти данные в баллистический калькулятор.
Надеюсь эти знания помогут вам правильно выбрать пули для ваших целей!
Все расчеты были произведены с использованием баллистического калькулятора Стрелок,
СОДЕРЖАНИЕ
Формулы
Общий
Баллистика
Коэффициент формы i может быть получен 6 методами и применяться по-разному в зависимости от используемых моделей траектории: G-модель, Beugless / Coxe; 3 Небесный экран; 4 Небесный экран; обнуление цели; Доплеровский радар.
Вот несколько методов вычисления i или C d :
Если n неизвестно, его можно оценить как:
Коэффициент лобового сопротивления также можно рассчитать математически:
C d знак равно 8 ρ v 2 π d 2 <\ displaystyle C _ <\ text
Из стандартной физики применительно к G-моделям:
я знак равно C п C грамм <\ displaystyle i = <\ frac
Коммерческое использование
Эта формула предназначена для расчета баллистического коэффициента в сообществе специалистов по стрелковому оружию, но не имеет значения для C b, Снаряд :
История
В 1753 году Леонард Эйлер показал, как теоретические траектории могут быть рассчитаны с использованием его метода применительно к уравнению Бернулли, но только для сопротивления, изменяющегося как квадрат скорости.
В 1844 году был изобретен электробаллистический хронограф, а к 1867 году электробаллистический хронограф имел точность в пределах одной десятимиллионной секунды.
Пробная стрельба
Многие страны и их вооруженные силы с середины восемнадцатого века проводили испытательные стрельбы с использованием крупнокалиберных боеприпасов для определения характеристик лобового сопротивления каждого отдельного снаряда. Эти отдельные испытательные стрельбы регистрировались и отражались в обширных баллистических таблицах.
Среди испытательных стрельб наиболее заметными были: Фрэнсис Башфорт в Вулвичских болотах и Шуберинессе, Англия (1864–1889) со скоростями до 2800 футов / с (853 м / с) и М. Крупп (1865–1880) из Friedrich Krupp AG в Меппен, Германия, компания Friedrich Krupp AG продолжала эти испытательные стрельбы до 1930 года; в меньшей степени генерал Николай В. Маевский, затем полковник (1868–1869) в Санкт-Петербурге, Россия; Комиссия по опыту Гавра (1873–1889) в Гавре, Франция, со скоростями до 1830 м / с (6004 фута / с) и Британская королевская артиллерия (1904–1906).
Способы и стандартный снаряд
Метод Башфорта
В 1870 году Башфорт публикует отчет, содержащий свои баллистические таблицы. Башфорт обнаружил, что сопротивление его испытательных снарядов варьировалось в зависимости от квадрата скорости ( v 2 ) от 830 футов / с (253 м / с) до 430 футов / с (131 м / с) и в зависимости от куба скорости ( v 3 ) от 1000 фут / с (305 м / с) до 830 фут / с (253 м / с). В своем отчете за 1880 год он обнаружил, что сопротивление изменяется на v 6 от 1100 футов / с (335 м / с) до 1040 футов / с (317 м / с). Башфорт использовал нарезные орудия 3 дюйма (76 мм), 5 дюймов (127 мм), 7 дюймов (178 мм) и 9 дюймов (229 мм); гладкоствольные орудия аналогичного калибра для стрельбы сферическими выстрелами и гаубицы стреляли удлиненными снарядами, имеющими оживальную головку радиуса 1½ калибра.
Метод Маевского – Сиаччи
Приблизительно в 1886 году Маевский опубликовал результаты обсуждения экспериментов, проведенных М. Круппом (1880). Хотя используемые снаряды с оживальной головкой сильно различались по калибру, они по существу имели те же пропорции, что и стандартные снаряды, в основном 3 калибра в длину с радиусом действия 2 калибра. Размеры стандартного снаряда составляют 10 см (3,9 дюйма) и 1 кг (2,2 фунта).
Баллистические столы
Таблицы Башфорта 1870 года были до 2800 футов / с (853 м / с). Маевский, используя свои таблицы, дополнил таблицами Башфорта (до 6 запретных зон) и таблицами Круппа. Маевский задумал седьмую ограниченную зону и расширил столы Башфорта до 1100 м / с (3609 футов / с). Маевский преобразовал данные Башфорта из имперских единиц измерения в метрические единицы измерения (теперь в единицах измерения СИ ). В 1884 году Джеймс Ингаллс опубликовал свои таблицы в Артиллерийском циркуляре Армии США M, используя таблицы Маевского. Ингаллс расширил баллистические таблицы Маевского до 5000 футов / с (1524 м / с) в пределах 8-й зоны ограниченного доступа, но все же с тем же значением n (1,55), что и 7-я зона ограниченного доступа Маевского. Ингаллс перевел результаты Маевского обратно в имперские единицы. Результаты британской Королевской артиллерии были очень похожи на результаты Маевского и расширили их таблицу до 5000 футов / с (1524 м / с) в 8-й зоне ограниченного доступа, изменив значение n с 1,55 до 1,67. Эти баллистические таблицы были опубликованы в 1909 году и почти идентичны таблицам Ингаллса. В 1971 году компания Sierra Bullet рассчитала свои баллистические таблицы для 9 ограниченных зон, но только в пределах 4400 футов / с (1341 м / с).
Модель G
За прошедшие годы возникла некоторая путаница в отношении принятых размеров, веса и радиуса оживальной головки стандартного снаряда G1. Это заблуждение может быть объяснено полковником Ингаллсом в публикации 1886 года «Внешняя баллистика в плане огня»; стр. 15, В следующих таблицах в первом и втором столбцах указаны скорости и соответствующее сопротивление в фунтах для удлиненного в один дюйм диаметром и с оживальной головкой в полтора калибра. Они были выведены из экспериментов Башфорта профессором А.Г. Гринхиллом и взяты из его статей, опубликованных в Proceedings of the Royal Artillery Institution, № 2, Vol. XIII. Далее обсуждается, что вес указанного снаряда составлял один фунт.
Другой метод определения траектории и баллистического коэффициента был разработан и опубликован Уоллесом Х. Коксом и Эдгаром Буглессом из DuPont в 1936 году. Этот метод представляет собой сравнение формы в логарифмической шкале, изображенной на 10 графиках. Метод оценивает баллистический коэффициент, связанный с моделью сопротивления таблиц Ингаллса. При сопоставлении фактического снаряда с радиусами калибра, нарисованными на Таблице № 1, будет получено i, а с помощью Таблицы № 2 можно быстро рассчитать C. Кокс и Бьюлесс использовали переменную C в качестве баллистического коэффициента.
В последние годы произошли огромные успехи в вычислении траекторий плоского огня с появлением доплеровского радара, персонального компьютера и портативных вычислительных устройств. Кроме того, более новая методология, предложенная доктором Артуром Пейса, и использование модели G7, используемой г-ном Брайаном Литцем, инженером по баллистике компании Berger Bullets, LLC для расчета траекторий пули хвостовой винтовки Spitzer, и программное обеспечение на основе модели 6 Dof улучшили прогноз. плоских траекторий.
Баллистический коэффициент что это
Прежде всего, позвольтре оговорить весь ряд допущений и отправных моментов, использованных в нижеприведенных расчетах.
0.5, веса 168 гран. Почему именно такой разбег скоростей? Выбран простым подбором, чтобы обесперчить изменение падения траектории именно в 1.0 МОА. Улавливаете, куда клоню? Пуля со «средним» БК, со средней для данного калибра начальной скоростью, вернее сказать с ее разнобоем, дающим 1-минутное вертикальное рассеивание.
Кстати, подобный размах скоростей не является чем-то из ряда вон выходящим, взгляните хотя бы вот на эти цифры: http://www.snipercountry.com/SinclairReloading.html
Неважнецкие у нас дела при БК = 0.2 и ниже, здесь вертикальное рассеивание удваивается, а при БК = 0.1 почти утраивается. А вот от 0.4 и выше величина рассеивания падает, но не так чтобы в разы, а всего лишь на четверть. График напоминает нисходящую экспоненту. Но не суть.
Практические выводы из теоретической байды
(хочу напомнить, что мы в 30-х калибрах, не экстраполировать на другие):
1. Пули с БК ниже 0.3 могут не принести счастья из-за заметного возрастания рассеивания.
Вот.
А теперь можно бить ногами.
Но не по голове.
Я ею ем и матерюсь.
А еще вот такую бредятину сочиняю.
PS: Извините, что не в «баллистике». Там третью неделю никого нет.
ИМХО БК пули и точность вещи прямо не связанные. Погоня за высоким БК есть борьба за настильность, при условии что ДАННАЯ пуля еще и дает хороший результат по точности из данного ствола.
Тут и увеличение дистанции прямого выстрела и уменьшение влияния ошибок в определении дистанции.
PS. Кстати, такую статью мы бы у себя на Guns.kz/gunsclub.com с удовольствием разместили бы.
Кстати лучше не в ФАК, а в Баллистику. Был у нас и такой раздел.
Хочу обратить Ваше внимание на ряд моментов, ставящих под сомнение справедливость сделанных выводов. Это обусловлено прежде всего неправильностью самих посылок.
2. Если все же мы учитываем сопротивление и расчитываем упрощенно как траекторию точки массы, то упущены следующие важные обстоятельства. Коэффициент сопротивления зависит от числа Маха, а ВС как одно из его производных зависит от скорости. С увеличением скорости ВС увеличивается и наоборот, причем довольно значительно. При сравнении траекторий без учета этого фактора результаты не могут быть признаны корректными.
4. В реальности ES (предельные варации скорости) не отражаются немедленно на бумаге, особенно это касается коротких дистанций. В коротком БР не борются за этот показатель. Чаще всего при замерах ES победителей их разброс может достигать 30 м/с, т.е. примерно тех цифр, от которых Вы отталкиваетесь. Это не мешает им собирать одну дырку. Именно поэтому в коротком БР никто не взвешивает заряды. Погрешность навески в 0.2 грана считается вполне приемлемой. Есть более важные факторы, влияющие на рассеивание и стрелки предпочитают заниматься ими.
У меня есть и свое мнение и опыт по данному вопросу, но я не считаю возможным его приводить, тем более когда об этом не просят.
ЗЫ: Если, конечно, уважаемый Флинт будет не против
У меня, к сожалению, нет никакой лаборатории, но проведение практических стрельб с определением БК, рассеивания пуль, замера Vо на каждом выстреле и Rv, могло бы установить оптимальную величину Rv для СО и охот. патронов, наладить надежный контроль за качеством выпускаемой заводами продукции.
Наше счастье в том, что большинство тестов по интересующим нас проблемам уже проведено
и нам остается только «поднять» их результаты.
Автор тестирует развиваемые давления пороха N130 в винтовке 6PPC. Приведу две первые группы первого дня тестов. Группы по 5 выстрелов на 100 ярдов. С каждым выстрелом навеска пороха намеренно увеличивается с шагом 0.3 грана.
(Пуля Euber 68FB. Капсюль Fed 205M)
Следующая группа, где автор продолжал увеличивать заряд.
объясните наконец, почему разброс начальных скоростей не влияет на кучность, и какой критерий важнее ошибки в навеске пороха при снаряжении патронов.
Вот то, о чём говорит ВВ в п.2:
«Коэффициент сопротивления воздуха cD является одним из наиболее важных аэродинамических коэффициентов:
Коэффициент сопротивления при нулевом рыскании является функцией числа Маха и в основном определяется экспериментальным путем
либо при тестировании в аэродинамической трубе, либо измерениями, сделанными при помощи Доплеровского радара.
Рис.: Коэффициент сопротивления для нулевого рыскания для двух военных пуль
M80 (кал. 7.62 x 51 НАТО)
SS109 (кал. 5.56 x 45)
Используя формулу
cDotest(B,Ma) = iDtest(B) * cDoG1(Ma)
можно получить для bc (подразумевая «стандартные» атмосферные условия)
bctest = l / iDtest(B) * mtest / d?test
Кстати как вам, уважаемые форумчане, крайнее предложение?
Возвращаясь к примеру flint-а:
Скорость пули на дальности до 500м упадёт примерно от 2,3 до 1,4 Мах. Взглянув на график, увидим,
что и коэфф. сопр. изменится с 0,3 до 0,4, ну и как следствие уменьшится БК.
По поводу разброса скоростей и ТП при стрельбе на сто ярдов: а чудес то никаких нет.
Калькулятор показывает снижение траектории в данном диапазоне скоростей
в районе 2 мм. на 100 ярдов.
Может, существуют такие же примеры практических отстрелов на средние и дальние дистанции в лабораторных условиях, кроме БР соревнований?
На мой взгляд, flint просто заострил наше внимание на вопросе, о которым никто из присутствующих на моей памяти не высказывался.
За что ему огромное спасибо. Даже учитывая на все указанные ВВ допущения, есть над чем подумать и что проверить.
Почему-то думается, что практика покажет. «. что никакие трактаты специалистов по внешней баллистике не в состоянии отменить их применение».
Нисколько не сомневаясь, что в этом вопросе бенчрестеры впереди планеты всей и учитывая опыт и результаты ВВ, на данном этапе лично мне, например,
интересно поймать на средних дистанциях не сотые и даже десятые доли МОА, а хотя бы их половинки
Оно и естественно, как следствие, что что на таких дистанциях влияние баллистики ничтожно и все превращается в сплошную математическую неопределенность. Это именно тот случай, когда «шумовые эффекты» перекрывают влияние изучаемого фактора.
Кстати вот пример, буквально из области шумовых эффектов. Где-то примерно в 15 км от района, где я живу находится перевалочный узел Canadian Pacific Railway. Поезда там ходят круглосуточно, разгружаются и гудят тоже круглосуточно. Но днем я их никогда не слышу (орет телевизор, у соседа лает собака и т.д.). Ночью же, когда все утихомиривается, эти гудочки очь даже слыхать. Почему? Влияние наводок значительно меньше. Вы уж простите за примитивность примера. Но зато наглядно.
Андрей, изменение навески влияет на точку попадания. В приведенных тестах средняя точка при второй группе сместилась по вертикали выше миллиметров на 5-7 (точнее сложно сказать по фото). Третья группа была прервана на двух выстрелах, которые тоже сместились по вертикали. Такой опытный стрелок как Geza конечно же не мог проигнорировать признаки опасного давления при последних двух выстрелах и прекратил тесты.
О самом патроне теперь. Более важные факторы при стрельбе на короткие дистанции (чем вариации скорости). Приведу некоторые из них не в порядке важности, поскольку не готовился, а что на ум пришло:
— Пуля. Качество и ее сочетаемость с конкретным стволом (геометрия и пр). Неподходящая или некачественная пуля будет убивать вашу кучность гораздо в большей степени, чем вариации скорости. Бенчрестеры говорят ‘такая-то пуля любит такой-то ствол’. Это действительно так. За годы высокоточной стрельбы сложились известные комбинации (типов/весов/ геометрий пуль к производителю ствола /шагу и числу нарезов/геометрии канала) ГАРАНТИРОВАННО обеспечивающие высокие результаты. Это возможно благодаря тому, что ведущие ствольные производители выдерживают качество и размеры на протяжении многих лет.
— Неправильно подготовленная или неподготовленная гильза. Даст все виды вариаций, полностью разрушающие ваши группы, являясь кстати одной из причине разницы начальной скорости.
Извиняюсь за объем. Понимаю, что описал не все и что эта писанина вызовет еще больше вопросов, но я все равно собирался как-нибудь чиркнуть статейку для журнала на подобные темы, так что предлагаю отложить серьезные вопросы подробности до ее появления, а то каждый из затронутых пунктов достоин небольшого томика.
Вам этот материал скорее всего знаком, но может некоторым присутствующим будет интересно. Тут люди зарылись в проблему поглубже, чем первые авторы:
http://www.vni.com/successes/threerivers.html
Да, это известный материал и действительно эту проблему некоторые лаборатории пытаются решить механическими путями.
В том-то и дело, что авторами теории кучной скорости утверждалось, насколько я понял, что этот эффект достигается только при какой-то одной определенной скорости. Это противоречит опыту БР, согласно которому существует несколько таких «точек» в диапазоне эффективной работы пороха в гильзе конкретного дизайна. Они не обязательно могут быть привязаны к скорости, поэтому я не уверен, уместно ли их даже называть «кучными скоростями» во множественном числе. Хотя некоторые бенчрестеры «пляшут» при настроенным заряде именно от конкретной настроенной скорости по причине того, что разница в партиях пороха делает привязку к навеске менее удобной базой. С другой стороны многие знаменитые стрелки, кто прагматично закупает сразу большую партию пороха и работает лет с ней и только с ней на протяжении многих лет, так же удобно «пляшут» и от навески. Можно было бы по идее исходить от давления, НО оно более сложно замеряется инструментально.
Баллистический коэффициент что это
Как летают пули #1 (БК или ложки не существует)
Пожалуй, нет в стрелковом мире другого понятия[1], вокруг которого было бы нагорожено столь много легенд, дурно понятых объяснений, обманутых ожиданий и обильных разочарований в мишени. Надо сказать, что с терминологией существует изрядная неразбериха, что пониманию не способствует.
Начнём с инженерно-физического определения. Любознательному читателю не составит труда найти в справочнике формулу БК, в которой бдительный читатель отметит букву «V». В переводе на человеческий язык, это значит, что «настоящий», инженерный БК зависит от скорости движения.
Для (очень неплохой) современной пули это выглядит примерно так:
Вывод #1: У пули нет абсолютного значения БК, а есть только значение БК для определённой скорости полёта.
Вывод #2: Торможение пули наиболее велико (минимальный БК) в области около скорости звука (≃1 Маха). При преодолении звукового барьера наблюдается резкий, принципиальный перелом в характеристиках сопротивления воздушной среды [3].
Отчего же, задастся вопросом внимательный читатель, некоторые производители пуль смело указывают один единственный БК для конкретного изделия? Ответ: граждане имеют в виду не инженерно-физический БК, который зависит от скорости, а «баллистический» БК (хотя и тут грешат против истины, на чём мы отдельно остановимся).
(все размеры в калибрах)
(все размеры в калибрах)
На следующем графике хорошо видно как аэродинамические качества стандартных пуль G1 и G7 одних и тех же калибра и массы соотносятся друг с другом и, в свою очередь, с реальностью.
График этот, однако, вводит в заблуждение; может сложиться впечатление, что модель G1 ни к чему не пригодна, а миллионы стрелков, использовавшие её за последние 100 лет лишь чудом попадали по цели. Для более реалистичного сравнения, нужно учесть два фактора:
1. Собственно баллистический коэффициент, который по определению должен компенсировать разницу в весе и геометрии между стандартной моделью и реальной пулей. Все значения графика G1 нужно масштабировать на БК.
2. Диапазон скоростей, характерных для современного лёгкого стрелкового оружия: при прицельной стрельбе, пули редко летают быстрее 1000 м/с или медленнее 200 м/с.
С учётом этих двух моментов, разница выглядит не в пример менее радикальной:
Чтобы понять что об этом всём думать, вспомним зачем затевался разговор, и вернёмся от теории к реальности. Стрелка интересует не сопротивление воздуха и не баллистические коэффициенты, стрелка интересует куда попадёт пуля.
Суровый снайпер Гуня делает для себя следующие наблюдения:
* В сверхзвуковом диапазоне модели G1 и G7 одинаково хорошо предсказывают траекторию; ошибка не превышает 1см до 900 м для G1 и 1100 м для G7.
* В транс-звуковом диапазоне (от 1.1 М и ниже; около 1300 м для этого калибра) у G1 начинаются серьёзные сложности, а в дозвуковом диапазоне проверку реальностью G1 не выдерживает вообще.
* G7, с другой стороны, держится молодцом, и до 1650 м (приблизительно 0.9 М скорости) ошибка в расчётах траектории не превышает 10 см.
С поправкой на разницу габаритов, наблюдения остаются, в сущности, те же. В транс-звуке (около 800-850 м) у G1 начинается значительное расхождение с правдой, вплоть до полной потери контакта с реальностью в дозвуковом диапазоне. G7 же, опять-таки, держится молодцом, с ошибкой менее 10 см вплоть до версты.
Стоит отдельно отметить, что модель G7 систематически имеет смысл только для пуль типа «boat tail», примерно такой формы:
Для пуль с цилиндрической хвостовой частью («flat base»)
однозначной разницы в достоверности между G1 и G7 не наблюдается; в зависимости от геометрии конкретной пули, G1 зачастую даёт лучшие результаты.
Терпеливый и любознательный читатель, дочитавший до этого места, наверняка задаётся вопросом. Двумя вопросами.
Ответы на эти вопросы ждите в следующих выпусках нашего альманаха.
_____________________
[1] За исключением, разве что, пресловутого «останавливающего действия пули».
[2] Здесь и далее для иллюстрации будут использоваться пули производства компании Lapua. Объясняется это не какой-то особенной личной привязанностью автора к продукции этой конторы (хотя пули, конечно, отличные), а тем, что Lapua предоставляет в публичном доступе подробнейшие экспериментальные данные по реальной баллистике каждого своего изделия, которые легко сравнивать с результатами разных методов расчёта траектории.
[3] К этому вопросу мы ещё вернёмся в следующих выпусках нашего альманаха.
[5] Кроме привычки, инерции мышления, и большого объёма наработанных методик и материалов, использующих G1, нельзя не учитывать и чисто коммерческий момент: из всех моделей [6], стандартная пуля G1 обладает наименее аэродинамичной формой. Как следствие, по сравнению с эдакой болванкой, значение БК реальной пули в численном выражении получается самым большим. Производители пуль и боеприпасов с большим удовольствием публикуют большие БК по G1; «в попугаях получается значительно длиннее».
[8] где, как мы узнаем в следующих выпусках нашего альманаха, сложностей и без того хватает.