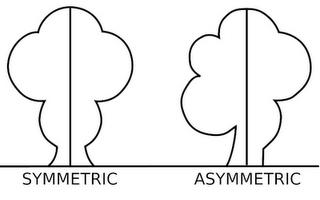
Асимметрия квадрата что это

Симметрия

Вам будет интересно: Как сдать физику и что нужно для этого сделать?

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Вам будет интересно: Гибкость: определение, средства и методы развития гибкости

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

История симметрии

Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

А философ Платон считал многогранники олицетворением четырех природных стихий:

Из-за всех этих теорий правильные многогранники называют телами Платона.

Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».

Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

Симметрия в природе

Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

Вывод

Источник

ОСНОВЫ КОМПОЗИЦИИ | Часть №3

ОСНОВНЫЕ СРЕДСТВА КОМПОЗИЦИИ

Средствами создания художественной формы являются: симметрия, асимметрия, пропорции, ритм,
масштаб, контраст, нюанс, т.е. явления, присущие природным формам.

Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.
/Г.Вейль/

Симметрия – равентсво, тождество, схожесть.
Симметрия предполагает неизменность не только самого объекта, но и каких-либо его свойств по отношению к преобразованиям, выполненным над объектом. Неизменность тех или иных объектов может наблюдаться по отношению к разнообразным операциям – к поворотам, переносам, взаимной замене частей, отражениям и т.д. В связи с этим выделяют разные виды симметрии.

Симметрии на плоскости бывают:
• Зеркальная симметрия — основывается на равенстве двух частей фигуры, расположенных одна относительно другой как предмет и его отражение в зеркале. Воображаемая плоскость, которая делит такую фигуру пополам, называется плоскостью симметрии.

• Осевая симметрия — связана с вращательным движением и повтором элементов вокруг оси симметрии, т. е. линии, при повороте вокруг которой фигура может неоднократно совмещаться сама с собой.

• Асимметрия значит отсутствие соразмерности, полное нарушение симметрии, повторяющиеся элементы отсутствуют или их нельзя совместить путём сдвигов или поворота.
• Диссимметрия – частичное нарушение симметрии. Диссимметрия хорошо воспринимается, так как, обладая структурными качествами симметрии, содержит больше свободы.

В композициях ритм может быть явным и скрытым:
• явный ритм очевиден, если, например, поместить элементы на полосатый фон;
• скрытый ритм представляет собой сложное чередование акцентов, иногда смысловых, направлений, технических приемов.

Существует метрический и ритмический порядок.
Метр и ритм в основе своей имеют симметрию. Но ритм, к отличие от метра, строится на основе разных, но повторяющихся элементов. В отличие от метрического повтора закономерность, на которой основан ритм, выражается в постепенных количественных изменениях в ряду чередующихся элементов – в нарастании или убывании чередований, объема или площади, в сгущениях или разрежениях структуры, силы тона и т.п.

Динамический ритмический ряд можно построить следующими способами:
• увеличением или уменьшением элемента по величине при одинаковых интервалах;
• возрастанием или убыванием интервала, но при одинаковых элементах;
• одновременным возрастанием или убыванием и элементов, и интервалов.
Обязательным условием при построении ритмического ряда должно быть ясное его прочтение. Поэтому элементы или интервалы должны повторяться не менее 3-5 раз.

Ритм проявляется, таким образом, в закономерном изменении порядка. Сбой ритма, как правило, ведет к серьезным нарушениям целостности, в то время как композиционно продуманное изменение в метрическом ряду не только возможно, но подчас во многих отношениях желательно.

Метр и ритм могут взаимно сочетаться.

✔️ МАСШТАБ ПРОПОРЦИЯ

Другие виды пропорциональных отношений:
— арифметическая прогрессия: 1, 3, 5, 7, 9…;
— геометрическая прогрессия: 1, 3, 9, 27, 81…;
— квадратичные отношения: 2, 4, 16, 256…;
— ряд Фибоначчи: 1, 2, 3, 5, 8… и др.

• МАСШТАБ
Масштабность – соразмерность принятому эталону. Существуют композиции, строящиеся на использовании мелкого масштаба, например, как на географических картах, и строящиеся
на крупных планах, например, фотографии макросъемки. Эффект создаваемой композиции зависит
от того, как выбранный масштаб и размер изображения соответствуют цели автора.
Важно заметить, что подсознательно эталоном для сравнения у человека является сам человек.

✔️ КОНТРАСТ НЮАНС ТОЖДЕСТВО

Одномерный контраст – контраст только по одному параметру, например по форме
Многомерный контраст – контраст по нескольким параметрам сразу: например, форма и цвет.

• Если элементы композиции сходны по форме, размерам, фактуре, пластике или другим свойствам, то в этом случае речь идет о тождестве.
Тождество – отношение полностью сходных объектов.
Используется несколько реже контраста и нюанса, так как обладает меньшими выразительными возможностями.

✔️ АКЦЕНТ ДОМИНАНТА АНАЛОГ

• Акцент — (лат. «ударение») – выделение, подчеркивание элемента, служит для выражения большей выразительности композиции. Чаще всего акцент выделяют цветом, формой (обычно малой, иначе акцент превратится в доминанту).

• Доминанта – это главный элемент композиции, которому подчиняются все остальные.

• Аналог (греч. «сходство») – уподобление (одинаковые или похожие друг на друга элементы в композиции). Аналоги придают композиции единство. Чаще всего бывают по цвету, форме, фактуре.

✔️ СТАТИКА ДИНАМИКА

• Статика – зрительное впечатление неподвижности.
Статика используется для выражения следующих смыслов: уверенность, спокойствие, остановка, «классика».
Статичные композиции могут характеризоваться симметрией, наличием четко выраженного центра и обязательно тяжестью и незыблемостью формы.
• Динамика – зрительное впечатление движения, скорости. Динамика используется для выражения смыслов: движение, энергия, сила, дерзость, порыв, «альтернатива».
Форму, активно односторонне направленную, как бы вторгающуюся в пространство, принято называть динамичной. Динамичность формы связана прежде всего с пропорциями. Равенство или нюанс отношений величин по трем координатам пространства характеризует относительную статичность формы. Контраст в отношениях создает динамику как «зрительное движение» в направлении преобладающей величины.

Статика и динамика не всегда взаимоисключают друг друга. В некоторых случаях можно говорить о внутренней динамике формы. Поэтому необходимо определить, что объективно доминирует – статичность или динамичность, так как композиция не может быть в одинаковой мере статичной и динамичной, что неизбежно ведет к утрате композиционной целостности.

✔️ ТЕКТОНИКА АТЕКТОНИКА

• Тектоника – установка на устойчивойсть. В отличие от статики, это не неподвижность. Динамичный, быстро и уверенно бегущий человек – тектоничен, так как не производит впечатления, что сейчас упадет.
• Атектоника – установка на неустойчивость. Атектоничны готические соборы, так как вся их неподвижная конструкция выражает стремление к полету.

✔️ КОМПОЗИЦИОННЫЕ ОСИ

Речь вдет не только об осях симметрии в ленточных композициях, являющихся всего лишь частным случаем композиционных осей, а в большей степени о тех направлениях развития композиции,
которые ведут взгляд зрителя, создавая впечатление движения или покоя.
Эти оси могут быть вертикальными, горизонтальными, диагональными и так называемыми перспективными. Вертикальная направленность дает торжественность, устремленность к духу, горизонтальность как бы демонстрирует зрителю неспешное движение, диагональность наиболее динамична, она подчеркивает развитие. Во взаимодействии с другими средствами композиции оси часто выступают и в комбинации между собой, образуя крестообразные, многоходовые, сложные связи.

Приемы композиции – это процесс обоснованного выбора и применения средств композиции, например: пропорционирование, ритмизация, масштабирование, контрастирование, нюансировка и т.д.

Источник

Осевая и центральная симметрия

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

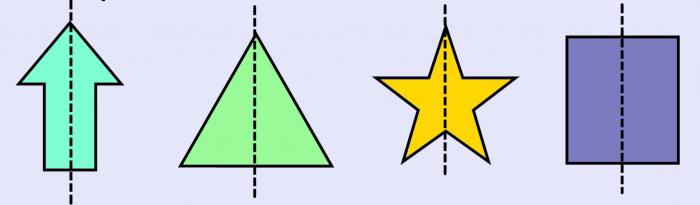
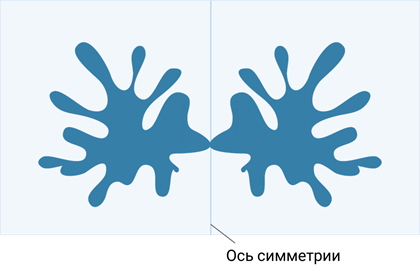
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

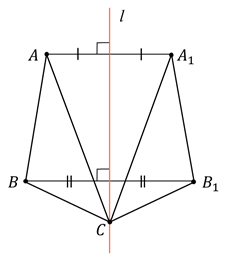
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

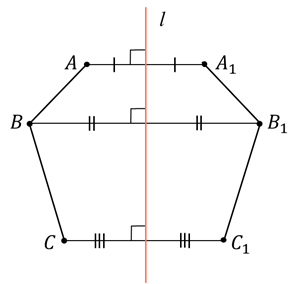
Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 2. Постройте треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра (точки О).

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Что такое симметрия и асимметрия?

Симметрия ассоциируется с гармонией и порядком. И не зря. Потому что на вопрос, что такое симметрия, есть ответ в виде дословного перевода с древнегреческого. И получается, что она означает соразмерность и неизменность. А что может быть упорядоченней, чем строгое определение местоположения? И что можно назвать более гармоничным, чем то, что строго соответствует размерам?

Что означает симметрия в разных науках?

Биология. В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии. Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.

Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.

Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.

Как определяют симметрию разные словари?

На вопрос, что такое симметрия, словарь Ожегова уже говорит об одинаковости в положении частей относительно точки, прямой или плоскости.

В словаре Ушакова упоминается еще и пропорциональность, а также полное соответствие двух частей целого друг другу.

Когда говорят об асимметрии?

Приставка «а» отрицает смысл основного существительного. Поэтому асимметрия означает то, что расположение элементов не поддается определенной закономерности. В ней отсутствует всякая неизменность.

В живой природе асимметрия играет важную роль. Причем она может быть как полезной, так и вредной. К примеру, сердце помещается в левую половину груди. За счет этого левое легкое существенно меньшего размера. Но это необходимо.

О центральной и осевой симметрии

В математике выделяют такие ее виды:

Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.

В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.

Какие фигуры являются симметричными?

Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.

Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.

Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.

Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.

К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.

Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.

У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.

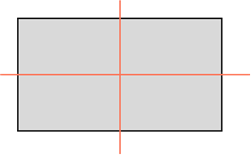
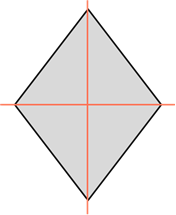
Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.

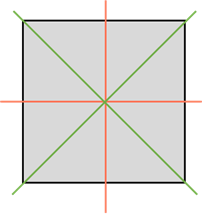
Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.

Источник

Симметрия

Урок 29. Наглядная геометрия 5–6 классы ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Симметрия»

Опыты с зеркалами, которые мы проводили на прошлом занятии, позволили нам прикоснуться к удивительному миру симметрии.

В переводе с греческого слово «симметрия» означает «соразмерность, пропорциональность, одинаковость в расположении частей».

Посмотрите на кленовый лист, бабочку, снежинку. Их объединяет то, что они симметричны. Если мы на каждом из рисунков начертим прямую вот таким образом…

А затем поставим зеркальце вдоль этой прямой на каждом рисунке, то отражённая в зеркале половинка фигуры дополнит её до целой (такой же, как исходная фигура).

Поэтому такая симметрия называется зеркальной (или осевой, если речь идёт о плоскости). Прямая, вдоль которой поставлено зеркало, называется осью симметрии.

Если симметричную фигуру сложить пополам вдоль оси симметрии, то её части совпадут.

С симметрией мы постоянно встречаемся в повседневной жизни. Люди используют симметрию в орнаментах, предметах быта, технике. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придаёт гармоничность, законченность. Симметрия также встречается в природе. Она создаёт ощущение порядка, гармонии, красоты.

Давайте сделаем кляксу. Для этого на лист бумаги капнем чернил. Сложим лист вдвое, а затем разогнём. Линия сгиба листа является осью симметрии кляксы.

Получается, что клякса имеет одну (вертикальную) ось симметрии.

А вот у снежинки 6 линий сгиба и все они являются осями симметрии.

У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.

Так, прямоугольник обладает двумя осями симметрии, каждая из которых проходит через середины двух его противоположных сторон. То есть, вырезав прямоугольник из бумаги и перегнув его по любой из двух осей симметрии, половинки фигуры совпадут.

Ромб также обладает двумя осями симметрии. Это прямые, которые содержат его диагонали.

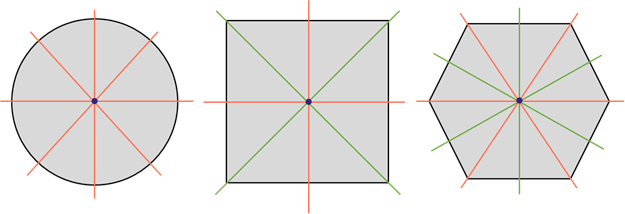
Квадрат имеет четыре оси симметрии. Две проходят через середины его противоположных сторон. И ещё две – это прямые, которые содержат его диагонали.

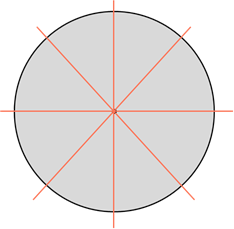
Круг. Его осью симметрии является любая прямая, которая проходит через его центр, то есть содержит диаметр круга. А значит, круг имеет бесконечно много осей симметрии

Теперь посмотрите на следующую фигуру. Это произвольный параллелограмм. У него нет ни одной оси симметрии.

У произвольного треугольника тоже нет осей симметрии.

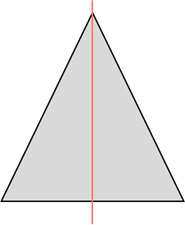
У равнобедренного треугольника есть одна ось симметрии.

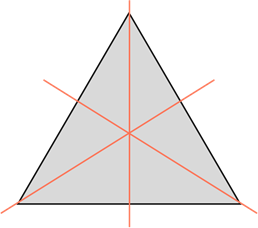
У равностороннего (то есть у правильного) треугольника – три оси симметрии.

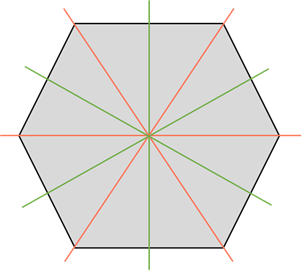
Теперь посмотрите на шестиугольник. У него три оси симметрии, которые проходят через противоположные вершины, и ещё три оси, которые проходят через середины противоположных сторон. То есть всего шесть осей симметрии.

Таким образом, мы можем сказать, что круг – «самая симметричная» фигура из рассмотренных, так как он имеет бесконечно много осей симметрии.

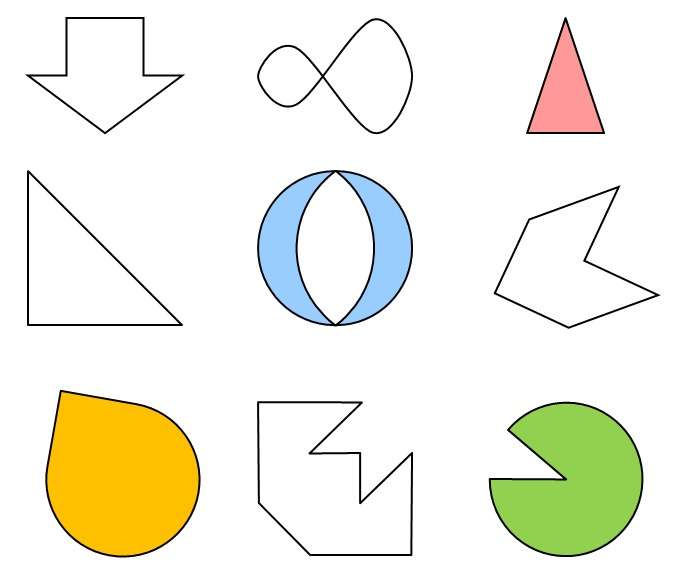
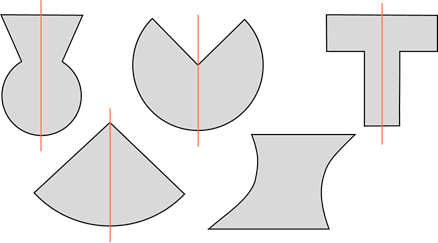
Сейчас давайте посмотрим на следующие фигуры и выясним, какая из них лишняя.

Итак, первая фигура напоминает замочную скважину. Она имеет одну ось симметрии.

Вторая фигура тоже имеет одну ось симметрии.

У третьей фигуры (в виде буквы Т) одна ось симметрии.

У четвёртой тоже одна. А вот пятая фигура не имеет ни одной оси симметрии. И поэтому она лишняя.

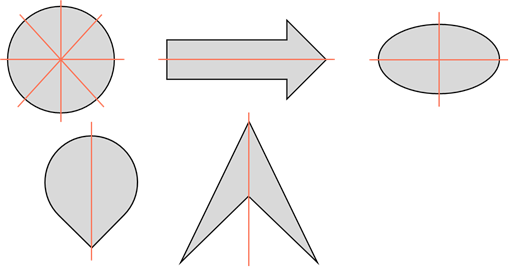
Теперь давайте посмотрим на следующие пять фигур. Что у них общего?

Первая фигура – круг. Выше мы выяснили, что у круга бесконечно много осей симметрии. Вторая фигура (в виде стрелки) имеет только одну ось симметрии. Третья фигура – эллипс. У эллипса две оси симметрии. Четвёртая фигура имеет одну ось симметрии. Пятая фигура тоже имеет одну ось симметрии. Каждая фигура имеет хотя бы одну ось симметрии.

На предыдущем занятии мы с вами проводили опыт с двумя плоскими зеркалами. С помощью составленного из двух зеркал калейдоскопа мы получали симметричные фигуры.

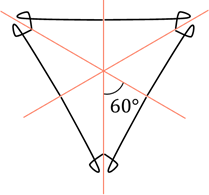
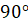
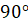
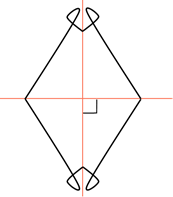
Давайте изобразим в виде прямых два зеркала под углом друг к другу. Затем нарисуем в одном из углов некоторую линию и, не пользуясь настоящими зеркалами, дорисуем её до симметричной фигуры, которая получилась бы при отражении в зеркалах. Полученная фигура имеет две оси симметрии. Понятно, что угол ними равен .

Посмотрите на рассмотренные выше фигуры, которые имеют две оси симметрии. Угол между осями равен .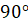

Если, например, мы поставим зеркала под углом 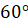друг к другу, то линия отразится 5 раз, а полученная фигура будет иметь 3 оси симметрии.

Давайте научимся точно строить отражение фигуры в зеркале. Представим, что прямая l – зеркало (или ось симметрии). Изобразим некоторую ломаную 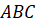и построим её отражение в зеркале.

Итак, из вершин , и опускаем перпендикуляры на прямую l. Затем продолжаем их «за зеркало» на такое же расстояние (равное длине соответствующего отрезка). Получаем точки , и . Соединяем эти точки. Ломаная является отражение ломаной .

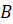
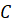
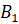
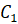
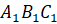
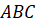
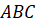
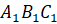
Можно сказать, что ломаная симметрична ломаной относительно прямой l.

Построим с вами треугольник, симметричный треугольнику 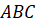относительно прямой l.

Из вершин и опустим перпендикуляры на прямую l. Затем продолжим их за прямую l на такое же расстояние (равное длине соответствующего отрезка). Получим точки и .

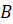
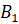
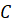
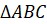
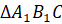
При этом точка осталась на месте. Она лежит на оси симметрии. Она симметрична сама себе. и симметричны относительно прямой l.

А сейчас посмотрите на рисунок.

Давайте выясним, симметрична ли точка точке относительно прямой l. Для этого мы соединим точки и . Затем с помощью угольника проверим, перпендикулярна ли прямая l отрезку . Перпендикулярна.

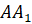
Потом с помощью линейки проверим, делит ли прямая l отрезок и пополам. Делит.

Значит, точки и симметричны относительно прямой l.

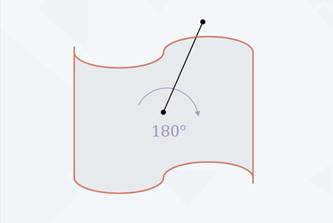
Кроме симметрии относительно прямой существует ещё симметрия относительно точки, так называемая центральная симметрия. Она характеризуется наличием центра симметрии – точки О, которая обладает определённым свойством. Можно сказать, что точка О является центром симметрии, если при повороте вокруг точки О на 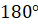фигура переходит сама в себя.

Понятие центральной симметрии распространяется и на трёхмерное пространство.

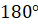
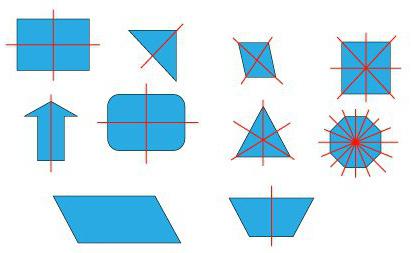
Проверить, является ли фигура центрально-симметричной или нет, можно с помощью обычной иголки и кальки. Наложим на нашу фигуру кальку. Затем, проколов фигуру в предполагаемом центре и обведя её контур, надо повернуть фигуру на вокруг иголки. Если фигура «вошла» в свой контур, то она центрально-симметричная.

Сейчас посмотрите на плоские фигуры, которые имеют и центр симметрии, и оси симметрии.

Это круг. Выше мы сказали, что он имеет бесконечно много осей симметрии, каждая из которых содержит его диаметр. А вот центром симметрии круга является его центр.

Квадрат имеет четыре оси симметрии. Центром симметрии квадрата является точка пересечения его диагоналей.

У шестиугольника шесть осей симметрии. Центром его симметрии является точка пересечения его диагоналей.

Выше мы сказали, что произвольный параллелограмм не имеет ни одной оси симметрии. Но он имеет центр симметрии – это точка пересечения его диагоналей.

А вот, например, равнобедренный треугольник имеет ось симметрии, но не имеет центра симметрии. То же самое можно сказать и про пятиугольник, у которого есть оси симметрии, но центра симметрии нет.

Источник