Аристотель когда открыл что земля круглая
Географические открытия Аристотеля
«Познание начинается с удивления»
Аристотель
Новые знания древние люди черпали из наблюдений. Подметив, что можно уверенно стоять на поверхности Земли, они осознали: планета плоска я — ведь иначе все падали бы, не ступив и шага! Кроме того, было «очевидно», что она имеет начало и конец. Никаких географических исследований и астрономических наблюдений тогда не проводили, поэтому ученые умы придумывали на этот счет самые разные небылицы.
Земля круглая?
Представления о форме нашей планеты кардинальным образом изменил древнегреческий ученый Аристотель. Во-первых, он стал первым смельчаком, который озвучил совершенно нелепую в те времена мысль: Земля — круглая. Во-вторых, он смог это доказать.
В 15 лет Аристотель осиротел. От отца ему досталось приличное наследство, которое будущее светило тратил на. книги. Еще в юности он привык много читать, что для его времени было редкостью. От других ученых Аристотеля отличало невероятное любопытство. Ему было недостаточно наблюдений: он всегда стремился понять причину происходящего. Книги научили Аристотеля рассуждать и устанавливать закономерности, позже перевернувшие представление о мире. Ученому не давала покоя мысль о форме Земли. Он не сомневался, что она не плоская, но озвучил свою догадку лишь после того, как собрал немало подтверждений своей версии.
Платон называл Аристотеля, любимого ученика, «умом своей школы». Однако тот порвал с идеалистическими взглядами наставника на мир, произнеся знаменитые слова: «Платон мне друг, но истина дороже».
Корабль и мачта
Наблюдая за приближающимся со стороны моря кораблем, Аристотель заметил, что сначала из-за горизонта появляются мачты и только потом выглядывает корпус. Это значит, что поверхность, по которой идет судно, округлая. Как ни странно, но такое утверждение многим показалось неубедительным.
Лунное затмение
К следующему доказательству Аристотель подошел с большей серьезностью. Наблюдая за лунными зат мениями, он каждый раз видел одну и ту же картину: на небесное тело «набегала» темная пелена и частично его закрывала. Для ученого было очевидно, что пелена ― это тень Земли, которую отбрасывает планета, оказавшись между Солнцем и Луной. Кроме того, Аристотель обратил внимание на одну важную особенность: сколько бы раз и в какое бы время он ни наблюдал лунное затмение, небесное светило всегда загораживала круглая тень, которая могла принадлежать только шару.
Другие научные открытия
Аристотель сделал немало судьбоносных для науки открытий. Так, опираясь на труды древнегреческого математика и астронома Евдокса, который был убежден, что планета на севере и юге нагревается не равномерно, он разделил земной шар в зависимости от продолжительности дня на пять климатических поясов: экваториальный («необитаемый вследствие жары»), два приполярных («необитаемые вследствие холода») и два промежуточных («умеренные, обитаемые»).
Таким образом ученый впервые определил географическую зональность. Кроме того, Аристотелю принадлежит немало исследований в области погоды и климата. Он первым за несколько сотен лет до нашей эры составил точнейшее описание круговорота воды в природе. Разрешив вопрос о форме Земли, греки заинтересовались ее размерами — но это уже другая история.
Шарообразная форма Земли: история открытия
У каждого народа формировались собственные представления о том, что представляет собой наша планета. Например, вавилоняне в VI тысячелетии до н. э. были убеждены: Земля — это одна большая гора, окруженная морем, на котором лежит небесная твердь; Солнце вечером прячется под землю и за ночь проходит путь с запада на восток, а утром поднимается на небо и катится в западном направлении по островкам суши — зодиакальным созвездиям, расположенным среди небесного моря.
Между тем китайцы, у которых искусство рисовать карты возникло еще за 1000 лет до н. э., не сомневались, что Земля прямоугольная и плоская, а небо над ней похоже на купол и держится на четырех колоннах. Пятую колонну, установленную посередине, сбил свирепый дракон, поэтому земля накренилась на восток, а небесная сфера — к западу, и все небесные тела устремились именно туда.
Индусы воображали Землю в виде громадной тарелки, покоящейся на слоновьих спинах.
В VII—VI вв. до н. э. древнегреческие мыслители Фалес Милетский, Анаксимандр и Анаксагор представляли, будто все человечество обитает то ли на гигантском пеньке, то ли на доске, то ли на обрубке дерева, которые покачиваются на морских волнах либо парят на подушке из сжатого воздуха. Собственно, на мысли о плоской планете их натолкнули знаменитые классические поэмы «Одиссея» Гомера и «Теогония» Гесиода, поэтому не удивительно, что описанная там картина мира надолго укоренилась в сознании людей.
Прошло два, три, четыре столетия, а серьезные натурфилософы, которые заложили основы учения о том, что вся материя состоит из микроскопических частиц-атомов, и слышали (в частности, от Аристотеля) гипотезы о шарообразности Земли, пытались доказать обратное. Скажем, Демокрит — автор идей бесконечности Вселенной и ее возникновения вследствие столкновений атомов — уверял: будь Земля круглой, Солнце по вечерам пряталось бы за дуговой, а не ровный горизонт. А Эпикур, который экспериментально изучал природу молний, ветров, землетрясений и пр., считал, тем не менее, что атомы падают на плоскую Землю из Космоса, словно снежинки, и так же, кружась, склеиваются между собой в разные крупные тела.
Среди христиан подобные воззрения бытовали вплоть до XVI века. К примеру, византийский купец Козьма Индикоплов в своей «Христианской топографии» описал Вселенную как сундук, внутри которого прячется прямоугольник тверди с горой на севере и морем вокруг. А в сборнике славянских духовных стихов «Голубиная книга» изложена легенда о китах, на которых держится весь мир.
Впрочем, знаменитый греческий математик Пифагор, который жил в VI—V вв. до н. э., за два столетия до Аристотеля, уже догадывался, что наша планета далеко не плоская, а с ним этими знаниями поделился моряк Скилак Кариандский. Аристотель же последовательно доказал предположения Пифагора: уходя за горизонт, суда не уменьшаются постепенно, а словно «проваливаются»; во время лунных затмений Земля отбрасывает на спутник круглую тень; в разных частях света люди видят не одни и те же звезды, то есть светила заслоняются Землей.
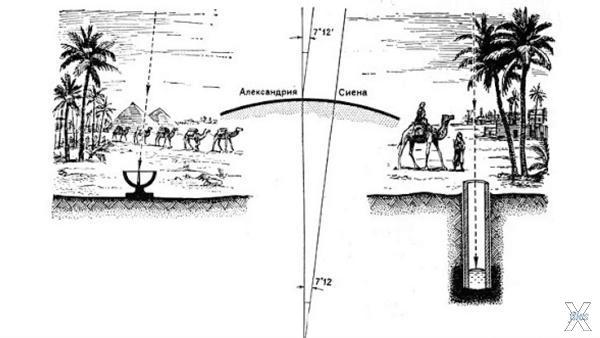
Последователю Аристотеля, Эратосфену, даже удалось определить радиус земного шара с погрешностью всего 1 %. Используя скафис — примитивный прибор для измерения углов, состоящий из шеста-гномона и чаши с делениями, — ученый сравнил положение Солнца в одно и то же время в северном египетском городе Александрия и в южной Сиене. На юге ровно в полдень гномон не отбрасывал тени (солнце стояло в зените), а на севере тень от шеста упала на чашу, показав 7,2-градусное отклонение от зенита. Эратосфен знал, что расстояние между двумя городами составляет 800 км, и на этом основании составил формулу: приравнял отношение полного угла (360°) и полученного (7,2°) к отношению неизвестной длины земной окружности и участка в 800 км. Расчеты показали, что экватор Земли простирается на 40 000 км, и, чтобы найти радиус, ученый разделил это число на удвоенное число пи, получив в итоге 6371 км.
Примерно в то же время греческий астроном Аристарх Самосский создал модель Солнечной системы, в которой Земля вращалась вокруг неподвижного Солнца и вокруг собственной оси. Согласно с традиционными взглядами, Аристарх воображал Вселенную заключенной в сферу с прикрепленными к ней звездами, но эта сфера, по его мнению, была практически безграничной. В том, что Земля не только похожа на шар, но и вращается вокруг своей оси, в 1520-х на горьком опыте убедилась команда путешественника Фернана Магеллана. Плывя на запад, моряки за четыре года обогнули всю Землю, но домой вернулись на день позже, чем рассчитывали: из-за того что планета крутится с запада на восток, корабли Магеллана постоянно притормаживали.
В том же XVI в. идею Аристарха на научном уровне поддержал польский астроном Николай Коперник (1473—1543) — в первой версии его знаменитого труда «Об обращении небесных сфер» даже было признание в том, что автор просто развил теорию великого грека.
В XVIII в. человечество заподозрило, что Земля не идеально круглая, а сплюснутая, только вот где — на полюсах или на экваторе, — не знал никто. Чтобы выяснить это, французы отправили в Перу и в приполярную зону две научные экспедиции, которые должны были провести разнообразные измерения местности и видимого небосвода. В результате выяснилось, что 1° меридиана (1/360 линии пересечения Земли с плоскостью, проходящей через ось вращения) на полюсе меньше, чем на экваторе — 110,6 против 111,9 км. Это могло означать одно: планету словно сжали сверху и снизу гигантскими ладонями, превратив в сфероид (вращающийся эллипс).
Кстати, пока французские ученые проводили полевые исследования, английский физик Исаак Ньютон (1643—1727) поставил воображаемый опыт: мысленно «прокопал» тоннели к центру Земли от экватора и от полюса, залил туда воды и «увидел», что экваториальную воду как бы выталкивает центробежная сила, направленная от центра планеты наружу перпендикулярно оси. Значит, заключил ученый, экваториальный тоннель должен быть длиннее полярного, дабы уравновесить жидкости. И чем быстрее крутится какое-либо тело, тем сильнее его сожмет. Впрочем, позже астрофизики выяснили, что всяческие перепады высот грунта и океанического дна делают Землю не идеально эллиптической, а несколько неровной. Эта форма была названа геоидом.
Что интересно, представители разных религий долгое время не могли смириться с идеей неплоской Земли (хотя, вопреки расхожему мнению, и не преследовали адептов «объемной» теории). В конце XIX в. в Англии даже было основано Общество плоской Земли, которое существовало вплоть до начала нашего столетия и с середины ХХ в. включало около 3000 членов. Все они свято верили в то, что астрономические наблюдения — ложь, для чего-то необходимая властям, а фотографии из космоса — наглая подделка.
Новое в блогах
Как древний учёный ещё 2260 лет назад смог доказать, что Земля имеет форму шара и назвал её размеры
Как древний учёный ещё 2260 лет назад смог доказать, что Земля имеет форму шара и назвал её размеры
С железобетонной уверенностью можно утверждать, что экспедиция под управлением Фернана Магеллана, совершив кругосветное плавание, абсолютно точно доказала, что наша планета имеет форму схожую с шаром. Увы, сам великий мореплаватель не дожил до возвращения в Европу. Однако и до этого плавания еще в античном мире была доказана шарообразность нашей планеты, причем шли ученые к этому поступательно.
В том что Земля имеет шарообразную форму был убежден величайший философ Древней Греции Платон (поскольку шар это идеальная форма), но доказать свои взгляды он так и не смог. А вот его ученик Аристотель пытался это сделать и достиг определенного успеха. Основных доказательств Аристотель приводил три, но, все они были скорее логическими, нежели строго научными.
Сами доказательства Аристотеля следующие:
1. С перемещением на север Полярная звезда становится все выше над горизонтом. Причем на юге можно увидеть звезды, которые никогда не видны на севере. Это возможно только в случае шарообразности Земли, если бы она была плоская, то все светила были бы видны везде одновременно на одной и той же высоте;
2. Созвездия на экваторе находятся высоко;
3. Если посмотреть на Луну во время ее затмения, то тень отбрасываемая Землей на это небесное тело всегда имеет круглую форму.
Полностью научно обоснованное доказательство шарообразности Земли с конкретными расчетами параметров произвел ученый из Александрии Эратосфен примерно в 240 году до Рождества Христова. Ему рассказывали, что в городе Сиена, расположенном на 5 000 стадий южнее на том же меридиане что и Александрия, в день летнего солнцестояния тень человека смотрящего в глубокий колодец закрывает в нем солнечное отражение. Проще говоря, в этот день предметы не отбрасывают тени, когда Солнце находится в зените.
А дальше в дело вступили простейшие измерения и законы геометрии. Фактически, единственным, что нужно было узнать Эратосфену, так это длину тени от некоего единичного измерительного шеста отбрасываемую им в день летнего солнцестояния в момент нахождения Солнца в зените. Вполне схожий эксперимент поставил дворецкий Брайтон в рассказе сэра Артура Конан Дойла «Обряд дома Месгрейвов».
Это измерение было проведено с помощью скафиса (чашеобразных солнечных часов, разделенных ученым на градусы) и мерного шеста гномона, с отверстием на конце, чтобы по яркой точке точнее проводить измерения тени.
Оказалось, что угол между Солнцем в зените в день летнего солнцестояния в Александрии составляет примерно 7,2 градуса или 1/50 часть круга. А вот в Сиене он в это время равен 0! Теперь можно было вычислить чему равна окружность земного шара.
Оставалось посчитать несложную пропорцию:
7,2/360 = 5 000/ х
Отсюда следует, х = 360*5 000/7,2 = 50*5000 =250 000 стадий.
Это и есть окружность нашей планеты. К сожалению, перевести используемые Эратосфеном стадии в привычные нам километры сейчас практически невозможно, поскольку неизвестно, каким именно стадием пользовался в своих расчетах древнегреческий ученый. В то время использовались стадии, которые нынче составляют 157,2 м, 172,5 м (египетский), 178 м (греческий) и 209,4 м (системы фараонов) соответственно. Были и другие стадии, в том числе олимпийский равный 192,27 м. Так что длина земной окружности по Эратосфену находится в рамках 40 000- 50 000 км.
Согласно нынешним данным длина земной окружности по меридиану (именно ее измерял Эратосфен) равна примерно 40 008, а по экватору около 40 075 км.
На этом древнегреческий ученый не остановился. Он знал формулу связи радиуса окружности с ее длиной:
L = 2 π*R где π= 3,14, а потому смог рассчитать радиус нашей планеты.
R = L/2π = 250 000/2*3,14 = 39 808 стадий.
При использовании стадия в 157,2 м получается 6302 км, при том что усредненный радиус Земли равен 6371 км.
Прошло еще примерно лет 200 и Страбон привел свое логическое доказательство шарообразности Земли — он первый обратил внимание на то, что нижняя часть корабля находящегося на линии горизонта не видна. А это возможно только из-за кривизны поверхности нашей планеты. Кстати, именно кривизна Земли ограничивает расстояние артиллерийского боя кораблей цифрой около 20 км при прямой видимости (немногим больше 100 кабельтовых).
Опубликовано 16 октября 2020 Комментариев 0 | Прочтений 496
Новое в блогах
Откуда древние греки знали, что Земля круглая
Любые спутниковые фотографии Земли в форме шара они объявляют фальшивками и происками участников заговора.
Если вам не доводилось слышать об общественном движении «Плоская Земля», позвольте выразить сожаление, что эту новость вы узнаете именно от нас: существует небольшая, но очень активная и шумная группа людей, которые искренне верят, что наша планета плоская. Любые спутниковые фотографии Земли в форме шара они объявляют фальшивками и происками участников заговора, организованного тайным мировым правительством.
В качестве главного доказательства своих утверждений, сторонники «Плоской Земли» выдвигают тот факт, что горизонт не выглядит изогнутым. Однако, вот что здесь самое странное: уже на протяжении двух тысячелетий человечеству известно, что Земля круглая, и для того, чтобы это выяснить, не потребовались никакие спутники.
Ради справедливости, следует признать: впервые древние греки предположили, что Земля имеет форму шара, еще до того, как у них появились веские доказательства. Первым ученым, который высказал гипотезу о шарообразной форме планеты еще в 500 году до нашей эры, считается философ и математик Пифагор. Однако, он сделал свое заключение на основании эстетических аргументов: по его мнению, сфера является наиболее совершенной формой.
Следует отметить, что Пифагор был, вероятно, первым западным мыслителем, предложившим эту гипотезу, однако, вполне возможно, что народы-мореплаватели, такие как древние полинезийцы, уже знали это. Столетие спустя, аналогичные мысли высказал великий древнегреческий философ Платон, что способствовало росту популярности этой новаторской идеи.
Как древние греки опередили Коперника
Но когда оказалось, что он ровно ничего не знает ни о теории Коперника, ни о строении солнечной системы, я просто опешил от изумления.
Артур Конан Дойл, «Этюд в багровых тонах»
Больше двух тысячелетий назад, в Древней Греции, астроном Аристарх Самосский пришёл к выводу, что Земля вращается вокруг Солнца. Постойте, постойте! Это же сделал Николай Коперник! И не два тысячелетия, а «всего» 500 лет назад. Это ведь он доказал, что все планеты вращаются вокруг Солнца. Или нет? Да, конечно, Коперник. Он установил это, опираясь на множество расчётов и наблюдений, на которые потратил 40 лет. Но первая гелиоцентрическая модель Солнечной системы была построена не им, а Аристархом, на 1800 лет раньше! Коперник знал о ней и строго подтвердил и обосновал эту модель.
Аристарху удалось невероятное — пользуясь элементарной геометрией, лишь наблюдая за небом, он придумал способ вычислить размеры Луны и Солнца и расстояния до них. И написал об этом книгу «О величинах и расстояниях Солнца и Луны». А разве так можно? Ведь Луна и Солнце очень далеко. Как узнать их размеры без современных приборов, без применения законов физики? Оказывается, можно, причём совсем простым рассуждением, доступным школьнику. Сейчас мы сами это проделаем. Найдём размеры Солнца и Луны, а потом вместе с Аристархом придём к выводу о том, что именно Земля должна вращаться вокруг Солнца, а не наоборот. Но Аристарху тогда никто не поверил. Почему? В этом мы тоже разберёмся. Но прежде чем измерять другие планеты и звёзды, надо измерить Землю.
Измеряем Землю
Кто первый высказал идею о шарообразности Земли, неизвестно. Возможно — Пифагор и его ученики, считавшие шар совершеннейшей из фигур. Полтора века спустя Аристотель приводит несколько доказательств шарообразности Земли. Главное из них: во время лунного затмения на поверхности Луны отчётливо видна тень от Земли, и эта тень круглая!
Эратосфен был крупнейшим учёным-энциклопедистом, занимался не только математикой, но и географией, картографией и астрономией. Он долгое время возглавлял Александрийскую библиотеку в Египте — главный научный центр того времени. Работая над составлением первого атласа Земли (конечно, не всей Земли, а известной к тому времени её части), он задумал провести точное измерение земного шара. Ведь чтобы составить карту, надо знать расстояния!
Идея была такова. К югу от Александрии, в городе Сиена (современный Асуан) один день в году, ровно в полдень, Солнце достигает зенита — высшей точки на небе. Исчезает тень от вертикального шеста, на несколько минут освещается дно колодца. Происходит это в день летнего солнцестояния, 22 июня — день наивысшего положения Солнца на небе. Эратосфен направляет своих помощников 2 в Сиену, и те устанавливают, что ровно в полдень (по солнечным часам) Солнце находится точно в зените. Одновременно (как написано в первоисточнике: «в тот же час») Эратосфен измеряет длину тени от вертикального шеста в Александрии. Получился треугольник, который на схематичном рисунке 2, а мы обозначили КАВ и перерисовали крупнее на рисунке 2, б. В Сиене солнечный луч перпендикулярен поверхности Земли, значит, если его продолжить, пройдёт через центр Земли. Параллельный ему луч в Александрии составляет угол с вертикалью, который мы обозначим буквой α. Такой же угол образуют радиусы Земли ZA и ZS, идущие из центра Земли в Александрию и Сиену. Семиклассники знают, почему — потому что накрест лежащие углы при параллельных прямых равны. А младшие пусть поверят нам на слово.
Теперь нарисуем круг радиусом 1 с центром на конце шеста — в точке K (рис. 2, в). Измерим длину дуги внутри угла α, обозначим её буквой d. На рисунке она выделена красным, а круговой сектор (то есть «долька» круга) — синим. Ему соответствует гигантский круговой сектор между радиусами Земли ZA и ZS, и он подобен синей «дольке», потому что имеет тот же угол α. Значит, дуга AS во столько раз больше дуги d, во сколько раз радиус Земли R = ZA больше радиуса маленького круга, равного 1. Итак, AS : d = R : 1. Длину d мы знаем (измерили). Как найти длину дуги AS? Это длина пути из Александрии в Сиену, около 800 км. Её Эратосфен аккуратно вычисляет, исходя из среднего времени движения верблюжьих караванов между двумя городами, а также используя данные бематистов — людей особой профессии, измерявших расстояния шагами. Поделив 800 км на длину дуги d, находим радиус Земли — примерно 6400 км. А длина окружности Земли равна 2πR = 40 000 км. Удивительно, что получилось столь круглое число! Разгадка проста: сама единица длины в 1 метр и была введена (во Франции в конце XVIII века), как одна сорокамиллионная часть окружности Земли (по определению!).
Эратосфен, конечно, использовал другую единицу измерения — стадий (около 200 м). Стадиев было несколько: египетский, греческий, вавилонский, и каким из них пользовался Эратосфен — неизвестно. Поэтому трудно судить наверняка о точности его измерения. Кроме того, неизбежная ошибка возникала в силу географического положения двух городов. Если города находятся на одном меридиане, то полдень в них наступает одновременно. Поэтому, сделав измерения во время наивысшего положения Солнца в каждом городе, мы получим правильный результат. Но на самом деле Александрия и Сиена — не на одном меридиане. Мы можем легко в этом убедиться, взглянув на карту, но у Эратосфена карты не было (ведь он как раз и составлял первую карту). Поэтому его метод (абсолютно верный!), скорее всего, дал неточный результат. Тем не менее, многие исследователи уверены, что точность измерения Эратосфена была высока и что он ошибался менее чем на 2%. Более точное значение было получено только через 2 тысячи лет, в середине XIX века. Над этим трудилась группа учёных во Франции и экспедиция В. Я. Струве в России. Даже в эпоху великих географических открытий, в XVI веке, люди не смогли достичь результата Эратосфена и пользовались неверным значением длины земной окружности. Ни Колумб, ни Магеллан не знали, каковы истинные размеры Земли и какие расстояния им придётся преодолевать. Они-то считали, что длина экватора гораздо меньше, чем на самом деле. Знали бы — может и не поплыли бы.
В чём причина высокой точности метода Эратосфена? До него измерения были локальными, на расстояниях, обозримых человеческим глазом, то есть не более 100 км. При этом неизбежны ошибки из-за рельефа местности, атмосферных явлений и т.д. Для большей точности нужно проводить измерения на очень больших расстояниях. Восьмисот километров между Александрией и Сиеной оказалось достаточно.
Опыт Эратосфена можно проделать и в наших широтах, где Солнце не бывает в зените. Правда, для этого нужны две точки обязательно на одном меридиане. Если же повторить опыт Эратосфена для Александрии и Сиены, сделав измерения в этих городах одновременно (сейчас это легко, можно послать SMS), мы получим верный ответ. И будет неважно, находятся ли города на одном меридиане (почему?).
Измеряем Луну и Солнце
Оказывается, измерить «подручными средствами» Луну и Солнце даже проще, чем Землю. Для этого не нужно уходить за 800 км, а можно всё сделать, не сходя с места. Мы повторим рассуждения Аристарха, попутно чуть поправив и упростив их.
Наши измерения будут состоять из трёх простых шагов. Сначала понаблюдаем за Луной.
Шаг 1. Во сколько раз Солнце дальше, чем Луна?
Почему иногда видна полная Луна, а иногда месяц? Потому что Луна светит отражённым солнечным светом. Если взять шар и посветить на него с одной стороны, то в любом положении освещённой окажется ровно половина шара. Так же и Солнце всегда освещает ровно половину поверхности Луны. Видимая форма Луны зависит от того, как повёрнута к нам эта освещённая половина. В новолуние, когда Луна вовсе не видна на небе, Солнце освещает её обратную сторону. Затем освещённая половина постепенно поворачивается в сторону Земли. Мы начинаем видеть тонкий серп, затем — месяц («растущая Луна»), далее — полукруг (эта фаза Луны называется «квадратурой»). Затем день ото дня (вернее, ночь от ночи) полукруг дорастает до полной Луны. Потом начинается обратный процесс: освещённая полусфера от нас отворачивается. Луна «стареет», постепенно превращаясь в месяц, повёрнутый к нам левой стороной, подобно букве «C», и, наконец, в ночь новолуния исчезает. Период от одного новолуния до другого длится примерно четыре недели. За это время Луна совершает полный оборот вокруг Земли. От новолуния до половины Луны проходит четверть периода, отсюда и название «квадратура».
Замечательная догадка Аристарха была в том, что, когда Луна в квадратуре, солнечные лучи, освещающие половину Луны, перпендикулярны прямой, соединяющей Луну с Землёй, то есть треугольник ZLS, соединяющий Землю, Луну и Солнце, — прямоугольный (рис. 3). Для простоты мы считаем, что наблюдатель находится в центре Земли. Это несильно повлияет на результат, так как расстояние от Земли до Луны и до Солнца значительно больше размеров Земли.
Рис. 3. Луна в квадратуре (схема)
Измерим угол β между лучами ZL и ZS во время квадратуры. Для этого надо одновременно видеть на небе Солнце и Луну: такое возможно, например, ранним утром. Затем нарисуем на большом листе другой прямоугольный треугольник с тем же углом β. Эти треугольники подобны. Измерив линейкой треугольник на листе, мы узнаем, что его гипотенуза в 400 раз больше катета. Значит, и в гигантском треугольнике ZLS гипотенуза ZS во столько же раз больше катета ZL. Таким образом, ZS = 400 ZL, значит Солнце в 400 раз дальше от Земли, чем Луна.
Аристарх получил отношение 20, а не 400, в первую очередь из-за того, что точно установить момент наступления квадратуры по внешнему виду Луны крайне трудно. И всё же наблюдение Аристарха впечатляет. Если бы, как тогда многие считали, Солнце и Луна были примерно на одном расстоянии от Земли, то в момент, когда Луна освещена наполовину, они находились бы недалеко друг от друга на небе, что совсем не так. Убедитесь в этом сами, посмотрев во время квадратуры днём на небо: положение Луны относительно Солнца позволит вам хоть немного лучше ощутить эти огромные масштабы.
Художник Мария Усеинова
1 Конечно, для этого надо обладать очень острым зрением и делать наблюдения в благоприятных условиях. Но в наше время, с помощью оптики с большим увеличением, это сделать легко. Видео «проседающего» на горизонте корабля есть в Интернете.
2 По легенде, одним из них был Архимед, друживший с Эратосфеном.