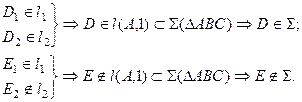Как доказать что прямая принадлежит плоскости
Как доказать что прямая принадлежит плоскости
Контрольные задания по теме:
Рабочая тетрадь задача 39, задача 40а, задача 40б
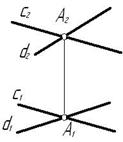
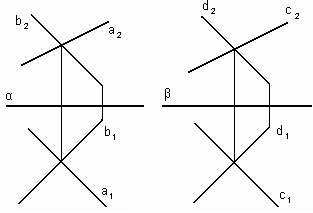
Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).
Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).
Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).
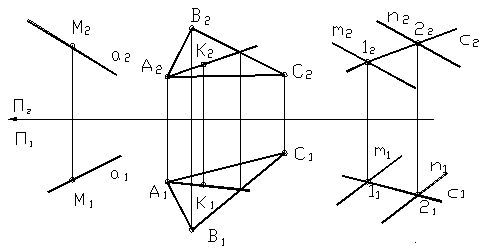
Рисунок 21
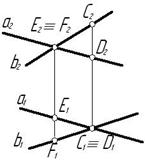
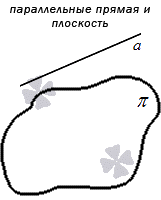
Прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. На рисунке 22 изображена прямая t, параллельная прямой b, принадлежащей плоскости Σ: t // b Î Σ (a Ç b).
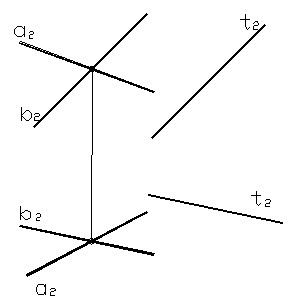
Рисунок 22
Через любую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости.
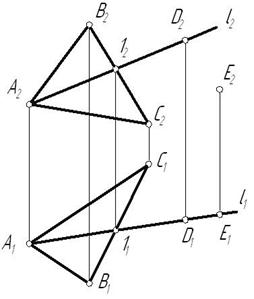
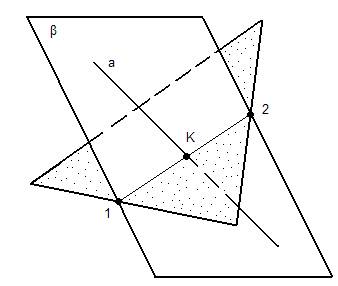
Это задача на определение общей точки прямой и плоскости. Её называют также точкой встречи. Рассмотрим пересечение прямой с плоскостью частного положения.
Плоскость Σ задана треугольником АВС и является горизонтально проецирующей плоскостью. Точка встречи прямой k с плоскостью Σ определяется по горизонтальной проекции. Фронтальная проекция точки К достраивается с помощью линии связи. Символическая запись будет выглядеть следующим образом: k Ç Σ (ABC) = K.
Видимость прямой относительно плоскости определяется при помощи фронтально-конкурирующих точек 1 и 2.
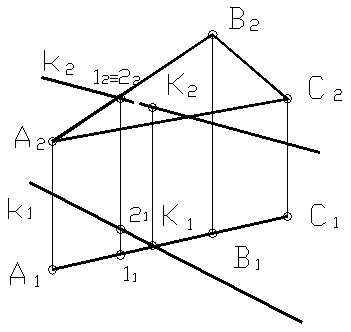
Рисунок 23
Пересечение прямой с плоскостью общего положения изображено на рисунке 24. В этом случае нужно заключить прямую в проецирующую плоскость.
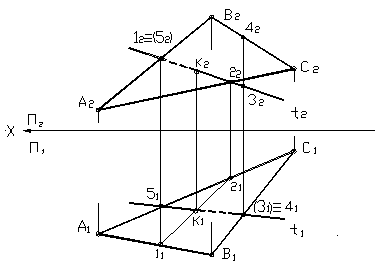
Рисунок 24
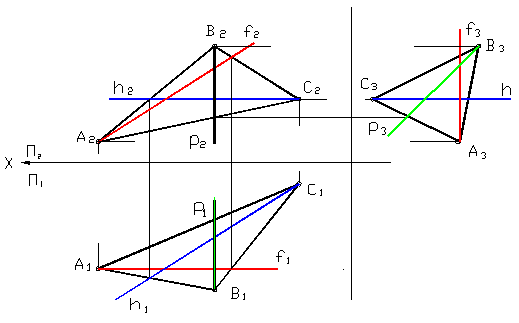
Рисунок 25
1. Сформулируйте условия принадлежности точки плоскости и прямой плоскости.
2. Как построить прямую параллельную заданной плоскости?
3. Вспомните этапы решения задачи на определение точки пересечения прямой и плоскости.
4. Какие точки называются конкурирующими?
5. Как провести в плоскости горизонталь и фронталь?
6. Какие еще особые прямые плоскости вы знаете?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Как доказать что прямая принадлежит плоскости
Сформулируем условие принадлежности прямой плоскости как аксиомы:
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.
Проиллюстрируем примерами использование этих аксиом.
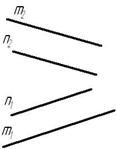
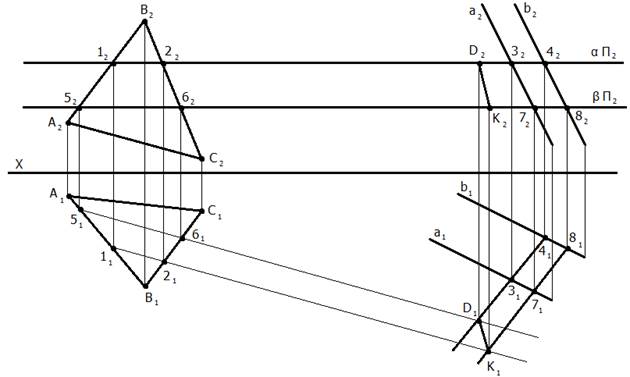
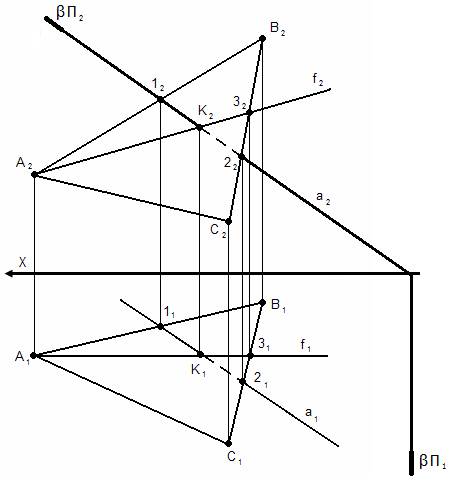
Требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.
Проекция прямой m2 пересекает проекции прямых n2 и k2 в точках В2 и С2 соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.
Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.
Рисунок 53. Прямая и плоскость имеют две общие точки
Задача. Через точку В провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис. 5 4).
Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k , значит согласно аксиоме 2 прямая принадлежит этой плоскости.
Принадлежность прямой и точки плоскости



Рис. 3.2 Взаимное расположение прямых
Прямые в пространстве могут занимать относительно друг друга одно из трех положений:
1) быть параллельными;
Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.
Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).
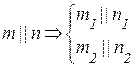
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная (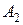
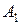
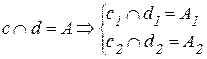
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.
На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).
Признак принадлежности точки и прямой плоскости:
Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.
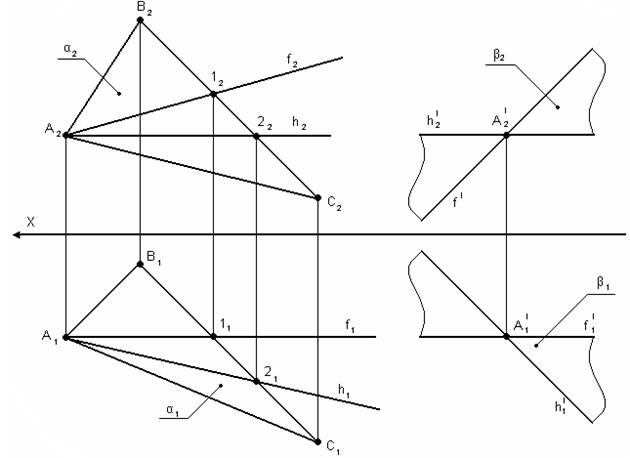
На рис. 3.5 изображена плоскость 
На рис. 3.6 показана плоскость 
Условие принадлежности прямой плоскости.
1. Прямая принадлежит плоскости, если две точки этой прямой принадлежат этой плоскости.
2. Прямая принадлежит плоскости, если она имеет с плоскостью одну общую точку и параллельна любой другой прямой, лежащей в этой плоскости.
2.2. Классификация плоскостей.
Положение плоскости относительно плоскостей проекции.
1. Плоскость общего положения – непараллельна и неперпендикулярна ни одной из плоскостей проекции.
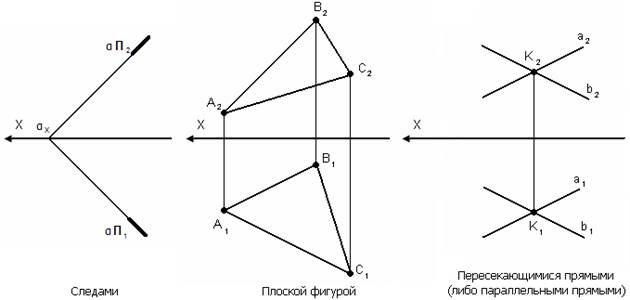
2. Плоскость уровня – плоскость параллельная какой-либо плоскости проекции;
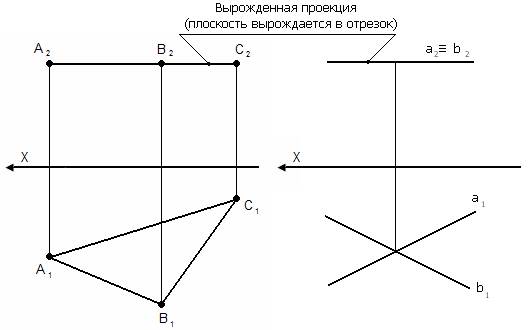
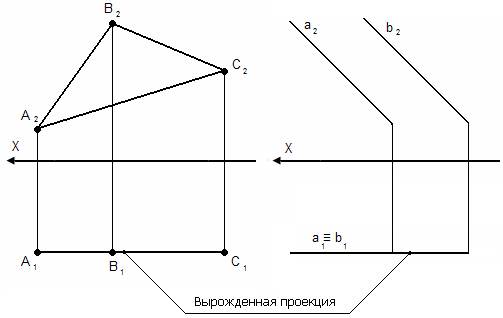
Вырожденная проекция обладает собирательными свойствами.
3. Плоскости проецирующие – перпендикулярны какой-либо плоскости проекции, но непараллельны другим плоскостям проекций;

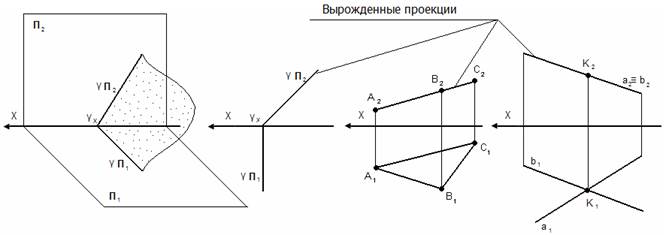
В) профильно-проецирующая – перпендикулярна П3, но непараллельна П1 и П2.
2.3. Взаимное расположение плоскостей
Плоскости могут быть относительно друг друга:
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Плоскости перпендикулярны, если прямая одной плоскости перпендикулярна каждой из двух пересекающихся прямых другой плоскости.
Плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.
2.4. Взаимное положение прямой и плоскости.
1) Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.
2) Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
3) Прямая может пересекать плоскость.
2.5. Главные линии плоскости.
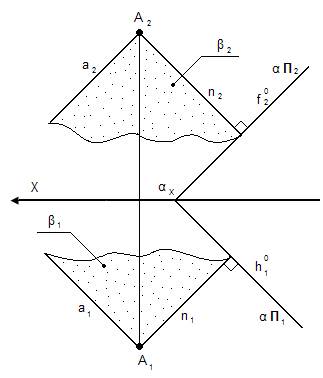
1. Горизонталь – прямая, лежащая в заданной плоскости и параллельная П1.
h 0 – нулевая горизонталь

Все горизонтали плоскости параллельны между собой и параллельны нулевой горизонтали (т.е. горизонтальному следу).
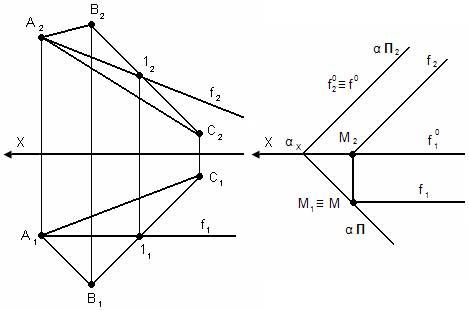
2. Фронталь – прямая, лежащая в заданной плоскости и параллельная П2.
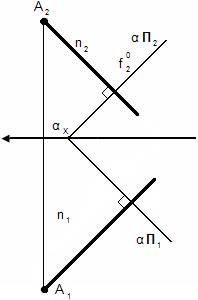
f0 – нулевая фронталь

Все фронтали плоскости параллельны между собой и параллельны нулевой фронтали (т.е. фронтальному следу).
Линия наибольшего наклона определяет угол наклона заданной плоскости к плоскости проекции П2 (расположена перпендикулярно всем фронталям).
Линия ската определяет угол наклона заданной плоскости к плоскости проекции П1 (расположена перпендикулярно всем горизонталям).
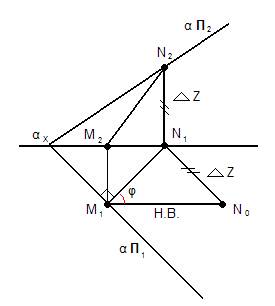
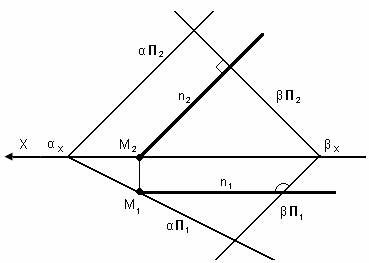
Задача. Определить угол наклона плоскости α к плоскости проекции П1.
M2N2 – фронтальная проекция линии ската
M1N1 – горизонтальная проекция линии ската
2. Для нахождения угла наклона необходимо определить угол наклона прямой MN к П1;
Для этого построим прямоугольный треугольник, который определит не только Н.В. MN, но и угол наклона его к плоскости проекции П1.
2.6. Линия наибольшего наклона к П2.
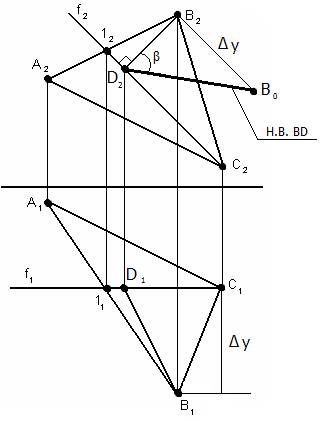
Для определения угла наклона плоскости АВС к плоскости проекций П2 необходимо определить Н.В. отрезка BD. Построения производим на той плоскости проекций, к которой необходимо определить угол наклона.
Лекция 3
Метрические и позиционные задачи.
3.1. Построение линии пересечения плоскостей.
Задача I-го типа.
Оба геометрических образа частного положения.
Проекции результата есть на чертеже и лежат на вырожденных проекциях проецирующих образов (построение не требуется).
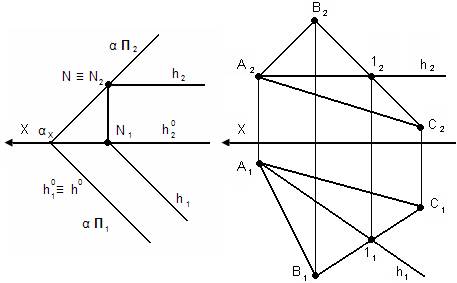
Пример: Построить линию пересечения плоскости α с плоскостью β.
α – горизонтально-проецирующая плоскость
β – горизонтальная плоскость уровня
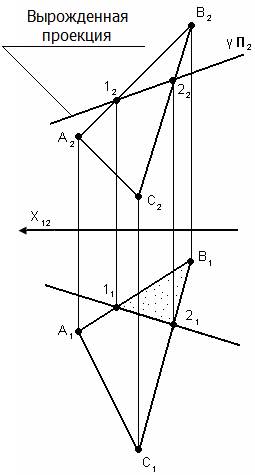
Один геометрический образ (ГО) частного положения, имеет вырожденную проекцию, а второй ГО общего положения (нет вырожденных проекций).
Одна проекция результата есть на чертеже и находиться на вырожденной проекции проецирующего образа (на П1 или П2), а другая определяется из условия принадлежности ко второму не проецирующему образу.
Пример: (АВС) – плоскость общего положения, γ – фронтально-проецирующая плоскость.
Задача III-го типа.
Оба ГО общего положения.
При помощи посредников. В качестве посредников выбираются ГО частного положения и решение задачи сводится к решению задачи II-го типа.
α – горизонтальная плоскость уровня, плоскость-посредник
3.2. Построение точки пересечения прямой с плоскостью.
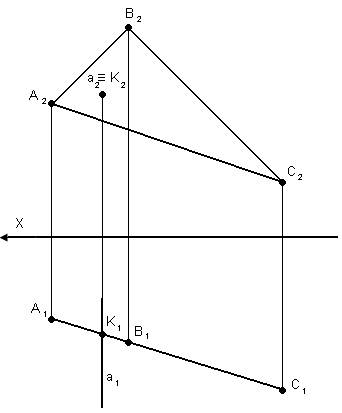
Оба геометрических образа частного положения.
Прямая а – фронтально-проецирующая
Проекция результата лежит на вырожденных проекциях проецирующих образов.
K1 – на вырожденной проекции треугольника АВС.
К2 – на вырожденной проекции прямой а.
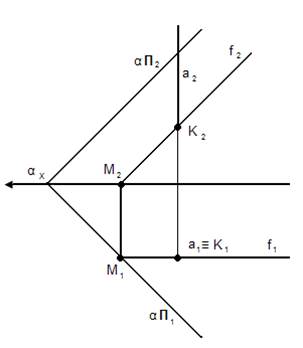
Плоскость задана следами.
Один ГО общего положения, второй частного положения.
α – плоскость общего положения.
Прямая а – горизонтально-проецирующая.
Горизонтальная проекция результата точка К1 лежит на вырожденной проекции прямой а, фронтальная проекция точки К2 определяется из условия принадлежности ко второму не проецирующему образу плоскости α.
Задача III-го типа.
Оба ГО общего положения.
Решаем при помощи посредника (плоскости частного положения).
1. Вводим плоскость-посредник β (β – частного положения и проходит через прямую а);
2. Определяем линию пересечения плоскости (АВС) – общего положения и плоскости β – частного положения. Решаем задачу II-го типа;
Решаем задачу II-го типа;
Лекция 4
Взаимно-параллельные и взаимно-перпендикулярные прямые и плоскости.
4.1. Построение прямой параллельной плоскости.
Для того чтобы провести через точку А прямую параллельную плоскости α необходимо:
1) в плоскости α выбрать или построить произвольную прямую;
2) через точку А провести новую прямую параллельную выбранной прямой.

Для того чтобы проверить, параллельна ли прямая плоскости необходимо попытаться в заданной плоскости построить прямую параллельную заданной. Если это удастся, то прямая и плоскость параллельны.
4.2. Построение параллельных плоскостей.
Для того чтобы через точку А провести плоскость параллельную заданной необходимо в заданной плоскости провести две произвольные пересекающиеся прямые и через точку А провести новые прямые, соответственно параллельные выделенным (удобнее всего использовать прямые частного положения – горизонтали и фронтали).
Для того чтобы проверить параллельны ли две плоскости необходимо попытаться построить в этих плоскостях пересекающиеся прямые, которые были бы попарно параллельны.
4.3. Построение прямой перпендикулярной плоскости.

4.4. Построение взаимно-перпендикулярных плоскостей.
Для того чтобы через точку А провести плоскость перпендикулярную заданной необходимо сначала построить прямую перпендикулярную заданной плоскости, а затем через эту прямую провести новую плоскость (решений бесконечное множество).
n – нормаль (перпендикуляр)
Для того чтобы проверить перпендикулярны ли заданные плоскости необходимо в одной плоскости попытаться найти или построить перпендикуляр к другой.

Лекция 5
Способы преобразования проекций.
Цель преобразований: ГО общего положения путем преобразования проекции привести к частному положению для упрощения решения метрических задач (нахождение площади, расстояния, углов).
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.
Параллельные прямые и плоскость – основные сведения
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.
Параллельность прямой и плоскости – признак и условия параллельности
Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.
Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.
Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.
Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.
Ответ: прямая с плоскостью параллельны.
Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.
Ответ: не параллельны.
Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:
Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.
Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:
Видим, что она не решаема, значит прибегнем к методу Гаусса.
Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.
Ответ: прямая и плоскость параллельны.